二分查找

二分查找分三种情况：

1. 寻找一个数（基本的二分搜索）

[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为3
返回 4

2. 寻找左侧边界的二分搜索

[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回： 1（第一个2的索引）

3. 寻找右侧边界的二分搜索

[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回： 3（最后一个2的索引）

1. 寻找一个数（基本的二分搜索）

• 查找的数不为重复元素

[1, 2, 2, 3, 4, 5, 6, 7] 查找元素为3

int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

2. 寻找左侧边界的二分搜索

[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回： 1（第一个2的索引）
找到 target 时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid] 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 检查出界情况
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}

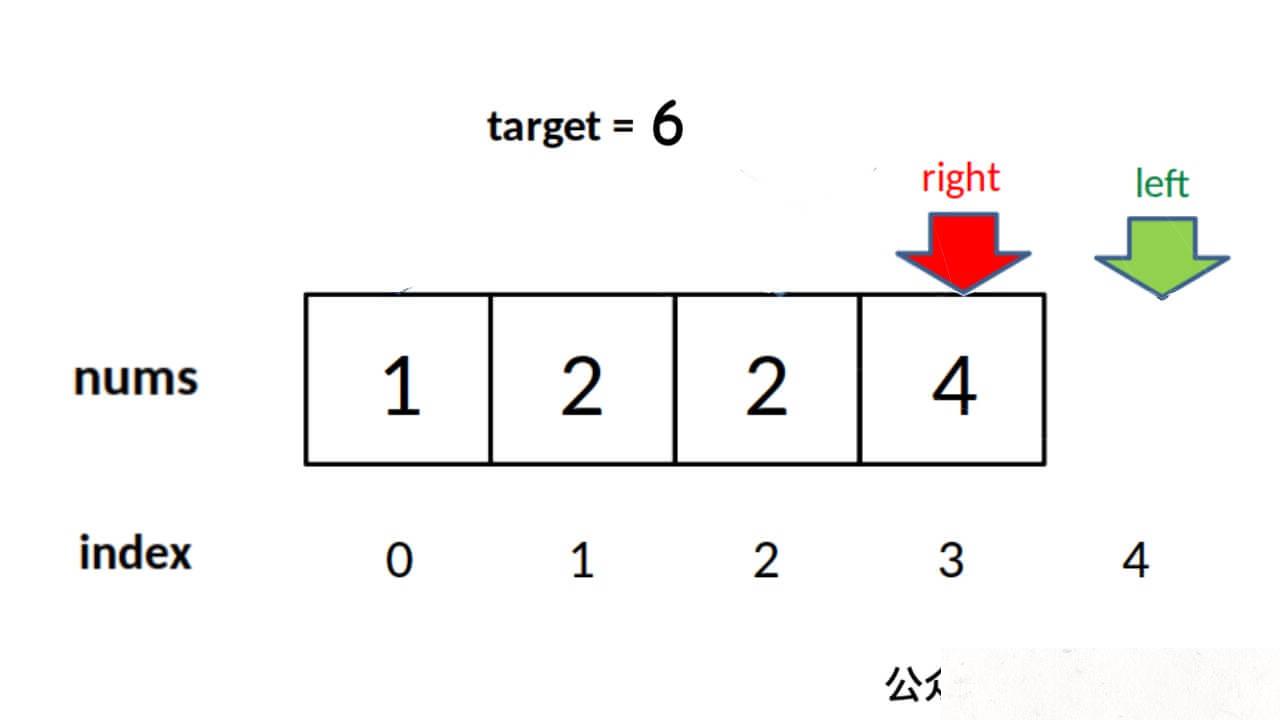
由于 while 的退出条件是 left == right + 1，所以当 target 比 nums 中所有元素都大时，会存在以下情况使得索引越界

因此，最后返回结果的代码应该检查越界情况

3. 寻找右侧边界的二分搜索

[1, 2, 2, 2, 3, 4, 5, 6, 7] 查找元素为2
返回： 3（最后一个2的索引）

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 这里改成收缩左侧边界即可
            left = mid + 1;
        }
    }
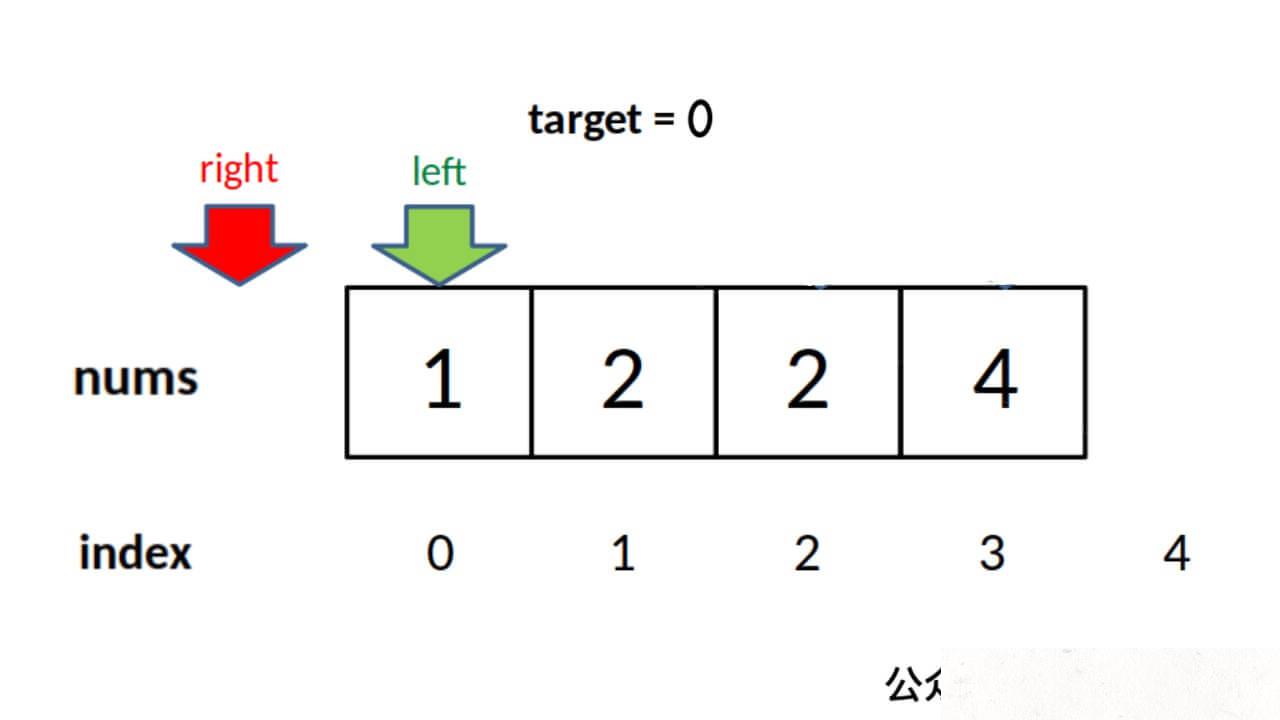
    // 这里改为检查 right 越界的情况，见下图
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

• 当 target 比所有元素都小时，right 会被减到 -1，所以需要在最后防止越界：
  

二分查找

原文：https://www.cnblogs.com/hugoyu/p/14678235.html