关键路径(C语言)

ltv 如果某时间不完成，会影响后续其它活动的开始）

lte 如果某时间不开始，则自身的剩余时间会不够用，影响后面顶点状态的完成时间点（从而推迟工期）

etv, ltv, ete, lte的运算关系

etv[n] 等于Vn的etv值 加上其后弧权值的和，可能存在多条路径，取最大值

ete 等于 etv[n] 因为etv事件的结束，也是以其后弧活动的开始

ltv[n] 等于Vn的ltv 减去 其前弧的权值，可能存在多条路径，取最小值（也就是以后面最大权值的弧为活动依据，否则会延期工程）

lte 等于 Vn的ltv 减去其前弧的权值（用此值和ete比较，如果相等则说明没有空闲，在工程的关键路径上）， 只计算一次

实现

图来自《大话数据结构》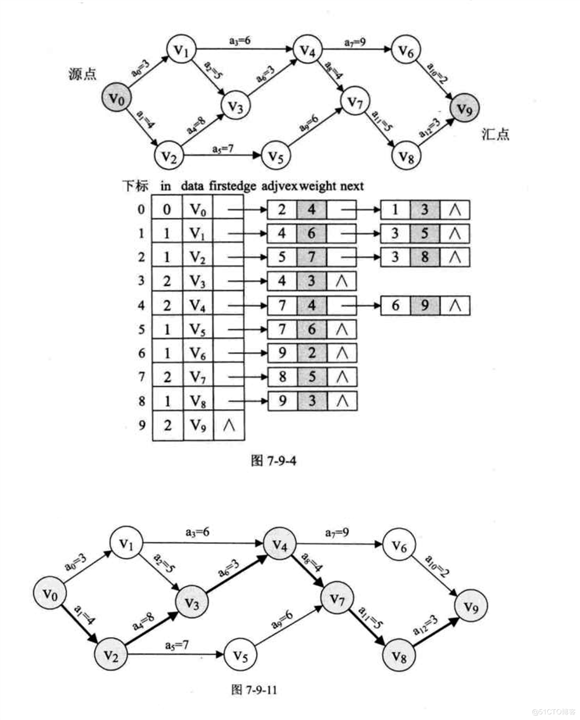

#include <stdio.h>
#include <stdlib.h>
/* 
 * 实现《大话数据结构》p287图7-9-11 关键路径
 */ 

#define MAXVEX 32

// 边表节点类型
typedef struct EdgeNode {
    int adjVex;
    int weight; // 弧的权值
    struct EdgeNode *next;
}EdgeNode, *PE;

// 顶点表节点类型
typedef struct VertexNode {
    int in; // 入度
    int data; // 顶点的数据，简单用数字标识
    PE firstEdge;
}VertexNode, *PV, AdjList[MAXVEX];

// 定义图
typedef struct {
    AdjList adjList;
    int numVertex, numEdge; // 未使用numEdge
}GraphAdjList, *PG;

// 全局变量
int ete, lte, *etv, *ltv;
int top2; // stack2的栈顶指针
int *stack2; // 复用拓扑排序的代码，把打印顶点改为入栈操作

void create(PG);
void topological(GraphAdjList);
void display(GraphAdjList);
void criticalPath(GraphAdjList);

void criticalPath(GraphAdjList graph)
{
    int i, gettop, k;
    PE e;
    // 初始化ltv
    ltv = (int *)malloc(sizeof(int)*graph.numVertex);
    for (i=0; i<graph.numVertex; i++) {
        ltv[i] = etv[graph.numVertex-1]; // ltv默认等于etv的最大值，即v9的etv
    }

    // 开始遍历, 计算ltv
    while (top2 != 0) {
         // 出栈，先输出的是V9顶点
         gettop = stack2[top2--];

         // 遍历出栈顶点的边表节点（V9的无边表节点，所以不会的进行此循环）
         for (e = graph.adjList[gettop].firstEdge; e; e = e->next) {
            // 保存节点下标
            k = e->adjVex;
            if (ltv[k] - e->weight < ltv[gettop]) // 取最小
                ltv[gettop] = ltv[k] - e->weight;
         }
    }

    // 比较ete lte找到关键路径
    printf("关键路径为:\n");
    for (i=0; i<graph.numVertex; i++) {
        ete = etv[i]; // 直接赋值
        for (e = graph.adjList[i].firstEdge; e; e=e->next) {
            k = e->adjVex;
            lte = ltv[k] - e->weight;
            if (ete == lte) {
                printf("<%d, %d>len[%d] -> ", i, k, e->weight); // 简单一些下村即顶点名
            }
        }
    }
    putchar(‘\n‘);

}
void display(GraphAdjList graph)
{
    int i, k;
    PE e;
    for (i=0; i<graph.numVertex; ++i) {
        printf("v%d, in %d, arcs:", graph.adjList[i].data, graph.adjList[i].in);
        e = graph.adjList[i].firstEdge;
        while (e) {
            k = e->adjVex;
            printf("->%d", graph.adjList[k].data);
            e = e->next;
        }
        putchar(‘\n‘);
    }
}

void topological(GraphAdjList graph)
{
    int i;
    int *stack; // 存放入度非0的顶点下标
    int top; // 栈顶指针下标
    int gettop; // 取栈顶
    int count; // 打印顶点(入度为0)计算器
    PE e;

    count = 0;
    top = 0; // 0为表示栈为空
    stack = (int *)malloc(sizeof(int) * graph.numVertex);
    // 先扫一遍，初始化栈
    for (i=0; i<graph.numVertex; i++) {
        if (graph.adjList[i].in == 0)
            stack[++top] = i;
    }

    // 添加etv stack2初始化
    top2 = 0;
    stack2 = (int *)malloc(sizeof(int) * graph.numVertex);

    etv = (int *)malloc(sizeof(int) * graph.numVertex);
    for (i=0; i<graph.numVertex; i++) {
        etv[i] = 0;
    }

    // 如果存在入度为0的顶点，则开始处理
    printf("拓扑序列:\n");
    while (top) {
        gettop = stack[top--]; // 出栈,同时更新栈顶指针
        printf("%d ", graph.adjList[gettop].data); // 打印顶点
        // 添加stack2入栈
        stack2[++top2] = gettop;
        count++;

        // 删除顶点相关的弧(操作为弧头顶点入度减1，如果减到0则弧头顶点入栈)
        e = graph.adjList[gettop].firstEdge;
        while (e) {
            i = e->adjVex;
            if (! --graph.adjList[i].in)
                stack[++top] = i;

            // 添加计算etv逻辑
            // 因为etv初始状态都是0，所以会依次更新顶点的etv值
            if (etv[gettop] + e->weight > etv[i])
                etv[i] = etv[gettop] + e->weight;

            e = e->next;
        }
    }

    putchar(‘\n‘);
    if (count == graph.numVertex)
        printf("拓扑排序成功, 无环\n");
    else
        printf("拓扑排序失败, 有环\n");

}

void create(PG g)
{
    int i;
    PE e;

    g->numVertex = 10;

    for (i=0; i<g->numVertex; i++) {
        g->adjList[i].data = i; // i即为顶点名Vi
        g->adjList[i].firstEdge = NULL;
    }

    // 填充邻接表(添加时顺序保持与书中7-9-4一致《大话数据结构》)
    // v0
    g->adjList[0].in = 0;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 2;
    e->weight = 4;
    e->next = g->adjList[0].firstEdge;
    g->adjList[0].firstEdge = e;

    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 1;
    e->weight = 3;
    e->next = g->adjList[0].firstEdge;
    g->adjList[0].firstEdge = e;

    // v1
    g->adjList[1].in = 1;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 4;
    e->weight = 6;
    e->next = g->adjList[1].firstEdge;
    g->adjList[1].firstEdge = e;

    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 3;
    e->weight = 5;
    e->next = g->adjList[1].firstEdge;
    g->adjList[1].firstEdge = e;

    // v2
    g->adjList[2].in = 1;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 5;
    e->weight = 7;
    e->next = g->adjList[2].firstEdge;
    g->adjList[2].firstEdge = e;

    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 3;
    e->weight = 8;
    e->next = g->adjList[2].firstEdge;
    g->adjList[2].firstEdge = e;

    // v3
    g->adjList[3].in = 2;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 4;
    e->weight = 3;
    e->next = g->adjList[3].firstEdge;
    g->adjList[3].firstEdge = e;

    // v4
    g->adjList[4].in = 2;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 7;
    e->weight = 4;
    e->next = g->adjList[4].firstEdge;
    g->adjList[4].firstEdge = e;

    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 6;
    e->weight = 9;
    e->next = g->adjList[4].firstEdge;
    g->adjList[4].firstEdge = e;

    // v5
    g->adjList[5].in = 1;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 7;
    e->weight = 6;
    e->next = g->adjList[5].firstEdge;
    g->adjList[5].firstEdge = e;

    // v6
    g->adjList[6].in = 1;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 9;
    e->weight = 2;
    e->next = g->adjList[6].firstEdge;
    g->adjList[6].firstEdge = e;

    // v7
    g->adjList[7].in = 2;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 8;
    e->weight = 5;
    e->next = g->adjList[7].firstEdge;
    g->adjList[7].firstEdge = e;

    // v8
    g->adjList[8].in = 1;
    e = (PE)malloc(sizeof(EdgeNode));
    e->adjVex = 9;
    e->weight = 3;
    e->next = g->adjList[8].firstEdge;
    g->adjList[8].firstEdge = e;

    // v9
    g->adjList[9].in = 2;

}

int main(void)
{
    GraphAdjList graph;
    create(&graph);
    display(graph);
    topological(graph);
    criticalPath(graph);

    return 0;
}

output

[root@8be225462e66 c]# gcc criticalPath.c && ./a.out
v0, in 0, arcs:->1->2
v1, in 1, arcs:->3->4
v2, in 1, arcs:->3->5
v3, in 2, arcs:->4
v4, in 2, arcs:->6->7
v5, in 1, arcs:->7
v6, in 1, arcs:->9
v7, in 2, arcs:->8
v8, in 1, arcs:->9
v9, in 2, arcs:
拓扑序列:
0 2 5 1 3 4 7 8 6 9
拓扑排序成功, 无环
关键路径为:
<0, 2>len[4] -> <2, 3>len[8] -> <3, 4>len[3] -> <4, 7>len[4] -> <7, 8>len[5] -> <8, 9>len[3] ->
[root@8be225462e66 c]#

关键路径(C语言)

原文：https://blog.51cto.com/sndapk/2720758