算符优先法:
根据这个运算优先关系的规定来实现对表达式的编译或解释执行的。
算数四则运算规则:
先乘除,后加减;,
从左算到右;
先括号内,后括号外;
任何一个表达式都是由操作数、运算符和界限符组成的,称之为单词。其中运算符和界限符统称为算符
算符间的优先关系
| + | - | * | / | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | > | < | < | < | > | > |
| - | > | > | < | < | < | > | > |
| * | > | > | > | > | < | > | > |
| / | > | > | > | > | < | > | > |
| ( | < | < | < | < | < | = | |
| ) | > | > | > | > | > | > | |
| # | < | < | < | < | < | = |
为了实现算符优先算法,可以使用两个工作栈。一个称为OPTR,用以寄存运算符;另外一个称做OPND,用以寄存操作数或运算结果;
算法的基本思想如下:
首先置操作数栈为空栈,表达式起始符“#”为运算符栈的栈底元素;
依次读入表达式中的每一个字符,若是操作数则进入OPND栈,若是运算符和OPTR栈的栈顶运算符比较优先权后作相应操作,直至整个表达式求值完毕。(即OPTR栈的栈顶元素和当前读入的字符均为“#”)。
求值过程:
1 OperandType EvaluateExpression(){ 2 //算数表达式求值的算符优先算法。 3 //设OPTR和OPND分别为运算符栈和运算数栈。 4 //OP为运算符集合 5 InitStack (OPTR); 6 Push(OPTR,‘#‘); 7 InitStack(OPND); 8 c=getchar(); 9 while(c!=‘#‘ || GetTop(OPTR)!=‘#‘){ 10 if(!In(c,OP)){ 11 Push(OPND,c); 12 c=getchar(); 13 }else{ 14 switch(Precede(GetTop(OPTR),c)){ 15 case ‘<‘://栈顶元素优先权低 16 Push(OPTR,c); 17 c=getchar(); 18 break; 19 case ‘=‘://脱括号并接收下一字符 20 Pop(OPTR,x); 21 c=getchar(); 22 break; 23 case ‘>‘://退栈并将运算结果入栈 24 Pop(OPTR,theta); 25 Pop(OPND,b); 26 Pop(OPND,a); 27 Push(OPND,Operate(a,ttheta,b)); 28 break; 29 }//switch 30 } 31 }//while 32 return GetTop(OPND); 33 }//EvaluateExpression
Operate是进行二元运算的函数,如果是编译表达式,则产生这个运算的一组相应指令并返回存放结果的中间变量;如果是解释执行表达式,则直接进行该运算,并返回运算结果。
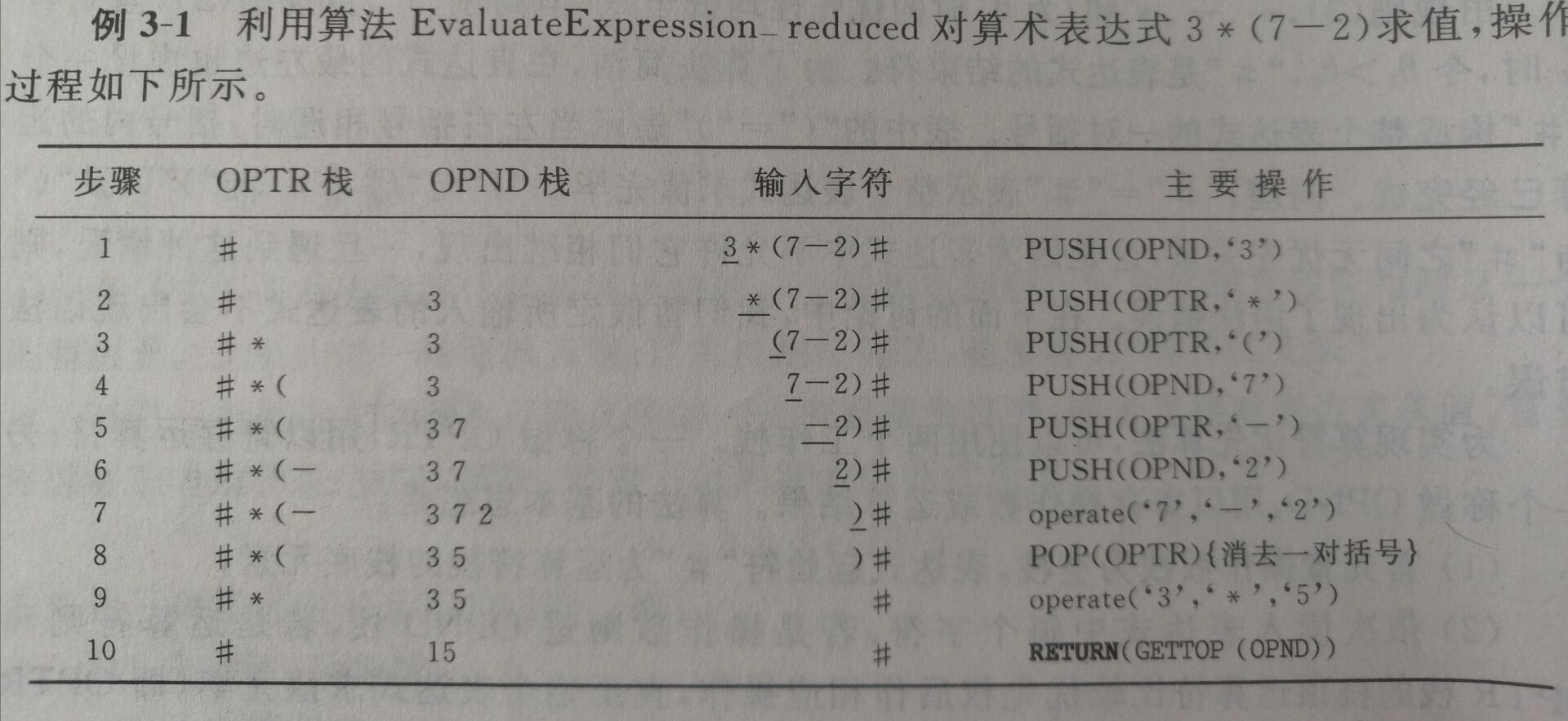
原文:https://www.cnblogs.com/zw-521/p/14689104.html