就是最近接触的项目是多标签文本分类类型,然后用bert做的,但是bert的评价标准只有准确率,然后组里大佬说光看准确率是不行的,准确率不能反应数据方面的东西,所以借此机会仔细研究一下F1评价指标。
准确率,顾名思义求法就是采用预测正确样本/全部测试样本,但是这样有一个缺点:数据不平衡时,无法很好的衡量分类器的好坏。故,我们研究接下来的评价指标F1。
精确率名字与准确率类似,但是二者不同,不同之处也恰巧体现在了“精“这一字。既然是“精”,则有精益求精的意思,所以他的求法就是被预测为正类的测试样本中真正是正类的测试样本(也就是预测正确的正类测试样本)/ 所有被预测为正类的测试样本。这就是精确率的求法,个人感觉精确率是衡量预测的好坏。
刚才说精确率是衡量预测的好坏的话,那么召回率就是针对样本数据而言的。话不多说直接看召回率的求法:被预测为正类的测试样本中真正是正类的测试样本(也就是预测正确的正类测试样本)/ 所有真正的正类测试样本。就是从所有正类样本中找回通过分类器之后仍是正类的样本。
Precision和Recall是一对矛盾的度量,一般来说,Precision高时,Recall值往往偏低;而Precision值低时,Recall值往往偏高。当分类置信度高时,Precision偏高;分类置信度低时,Recall偏高。为了能够综合考虑这两个指标,F-measure被提出(Precision和Recall的加权调和平均),即:
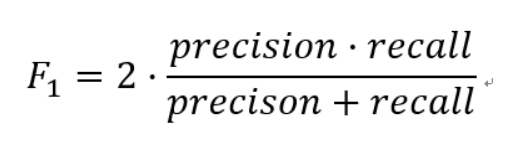
F1的核心思想在于,在尽可能的提高Precision和Recall的同时,也希望两者之间的差异尽可能小。F1-score适用于二分类问题,对于多分类问题,将二分类的F1-score推广,有Micro-F1和Macro-F1两种度量。
虽然刚才介绍了如何求精确率、召回率、F1-score,但是可能对于如何求还真不知道如何做。所以这里继续介绍,方便我们更容易求解。
在这里先介绍几个基本概念
有了这几个概念就可以将我们刚才介绍的公式更新为:

虽然我们添加了基本概念但是TP、FP、FN 这几个数值并不好求,但是混淆矩阵恰好可以将这些很好的展示出来。
混淆矩阵是机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。其中矩阵的行表示真实值,矩阵的列表示预测值。
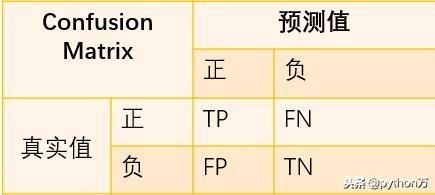
以上这个图是一个二分类的混淆矩阵,很简单,TP、FN、FP很容易就看见了。但是要是多分类的话
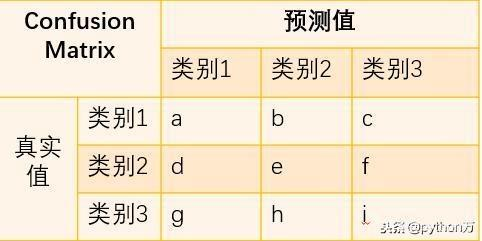
要是不了解规律就不能直接发现每个类别的TP、FN、FP。
这里在告诉大家如何快速找出我们需要的TP、FN、FP之前,先说一下混淆矩阵的特点:
混淆矩阵的每一列代表了预测类别,每一列的总数表示预测为该类别的数据的数目。混淆矩阵的每一行代表了数据的真实归属类别,每一行的总数表示为该类别的数据实例的数目。然后说一下我自己总结的规律,这里主要针对多分类而言,二分类显而易见就不说了:
混淆矩阵的对角线就是TP。混淆矩阵的每一列之和减去各列在对角线上的数值就是FP。混淆矩阵的每一行之和减去各行在对角线上的数值就是FN。以上的经验就是可以帮助我们快速从混淆矩阵中找到TP、FP、FN。所以接下来获得混淆矩阵就是我们接下来的关键。
这里由于本人太菜,本来想自己实现,但是只实现了二分类的,多分类没成功,然后成功加入调包侠阵营,真香啊hhh。
这里主要是针对多标签和多分类来讲
# 多分类
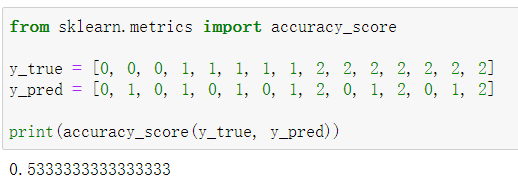
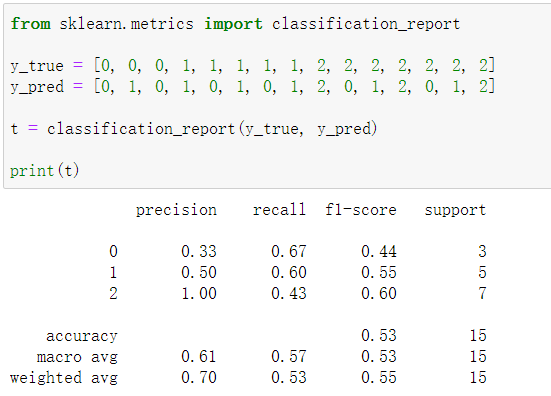
y_true = [0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2]
y_pred = [0, 1, 0, 1, 0, 1, 0, 1, 2, 0, 1, 2, 0, 1, 2]
# 多标签
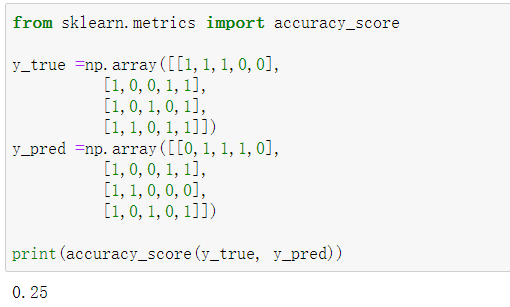
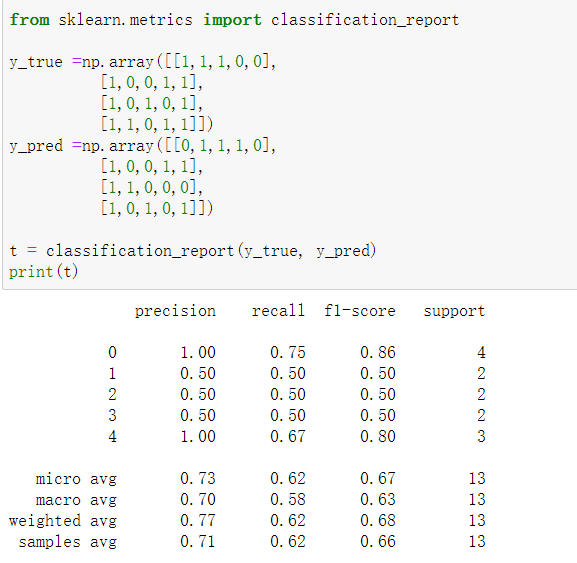
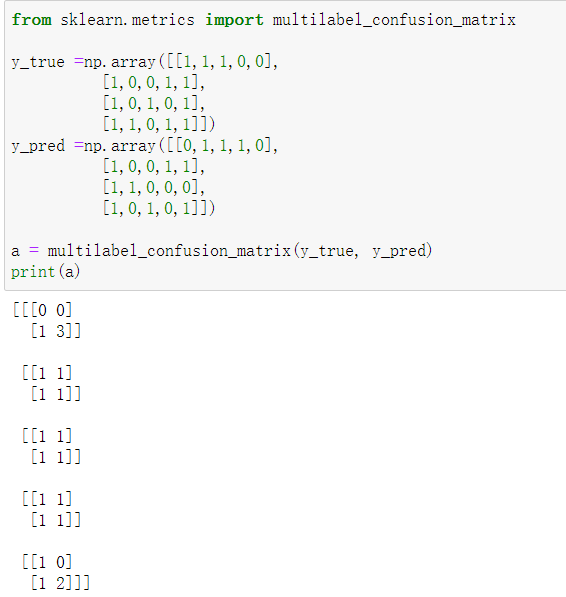
y_true =np.array([[1,1,1,0,0],
[1,0,0,1,1],
[1,0,1,0,1],
[1,1,0,1,1]])
y_pred =np.array([[0,1,1,1,0],
[1,0,0,1,1],
[1,1,0,0,0],
[1,0,1,0,1]])
功能:计算准确率
多分类:
多标签:
功能:建立一个显示主要分类指标的文本报告。
多分类:
多标签:
功能:计算混淆矩阵以评估分类的准确性。(只针对多分类和二分类,不包括多标签)
多分类:

功能:为每个类别或样本计算一个混淆矩阵。(特别适合多标签)
多标签:
功能:混淆矩阵可视化。(多标签可视化不了)
多分类:
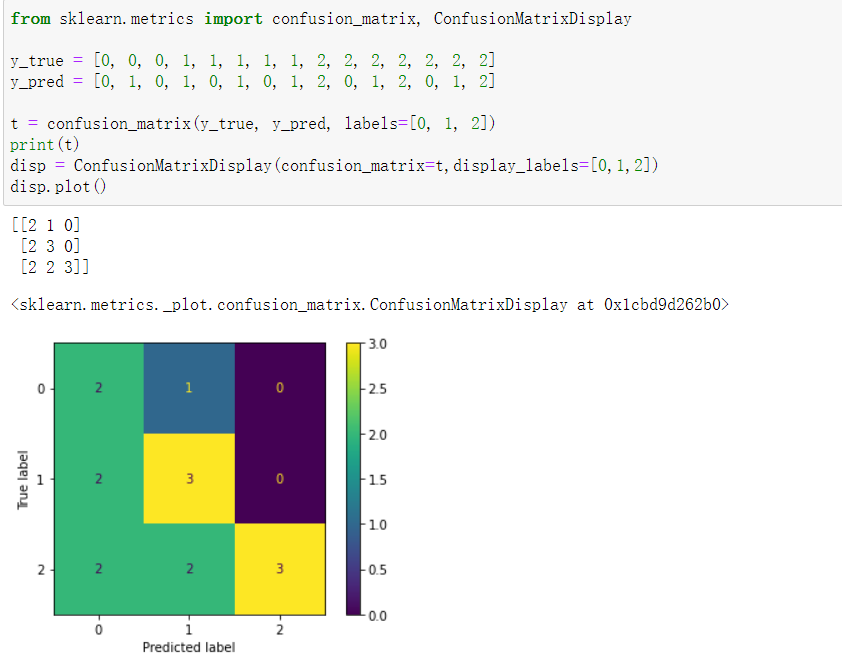
原理这回是明白了,可能还要再想想多标签的混淆矩阵是个什么原理。然后还是要尝试一下自己用python去实现一下多分类和多标签的f1评价指标以及他们的混淆矩阵。
实习Learning记录(九)——文本分类评价指标F1原理解析
原文:https://www.cnblogs.com/lzyrookie/p/14691269.html