有限元法(finite element method)是一种高效能、常用的计算方法。有限元法在早期是以变分原理为基础发展起来的,所以它广泛地应用于以拉普拉斯方程和泊松方程所描述的各类物理场中(这类场与泛函的极值问题有着紧密的联系)。自从1969年以来,某些学者在流体力学中应用加权余数法中的迦辽金法(Galerkin)或最小二乘法等同样获得了有限元方程,因而有限元法可应用于以任何微分方程所描述的各类物理场中,而不再要求这类物理场和泛函的极值问题有所联系。基本思想:由解给定的泊松方程化为求解泛函的极值问题。
将连续的求解域离散为一组单元的组合体,用在每个单元内假设的近似函数来分片的表示求解域上待求的未知场函数,近似函数通常由未知场函数及其导数在单元各节点的数值插值函数来表达。从而使一个连续的无限自由度问题变成离散的有限自由度问题。用有限个单元将连续体离散化,通过对有限个单元作分片插值求解各种力学、物理问题的一种数值方法。有限元法把连续体离散成有限个单元:杆系结构的单元是每一个杆件;连续体的单元是各种形状(如三角形、四边形、六面体等)的单元体。每个单元的场函数是只包含有限个待定节点参量的简单场函数,这些单元场函数的集合就能近似代表整个连续体的场函数。根据能量方程或加权残量方程可建立有限个待定参量的代数方程组,求解此离散方程组就得到有限元法的数值解。有限元法已被用于求解线性和非线性问题,并建立了各种有限元模型,如协调、不协调、混合、杂交、拟协调元等。有限元法十分有效、通用性强、应用广泛,已有许多大型或专用程序系统供工程设计使用。结合计算机辅助设计技术,有限元法也被用于计算机辅助制造中。
瞬态动力学分析需要求解半离散的方程组,离散意指结构由离散的节点描述,半离散是指在方程的导出过程中,每个时刻都要满足平衡。在瞬态分析中,连续的时间周期分为许多时间间隔,并且只有在离散的时间上才能得到解。
对于线性动力学问题,动力学行为完全由两个独立的特性决定:线弹性(动力)结构行为和施加的动力载荷。因此,可首先不考虑施加的载荷进行结构动力分析(即模态分析)来确定特征值;其次基于结构的特征值和特征模态计算给定载荷历程的结构动力响应。这一过程称为模态分析或模态叠 加法。由于高阶模态不准确,因而比较成功的应用大都在于由低频范围的激振的结构。
另一种方法,动力学方程可以作为施加载荷的函数而直接积分,积分方法有多种,重要的一点就是稳定性和精度,这些方法可以用于短波长问题,只要有限元网格足够细密,就能够描述这些局部的现象。
底板:碳钢材料,密度ρ=2850kg/m3,弹性模量E=210Gpa,泊松比v=0.28;底板几何参数,底板长度x宽度=1mx1m,厚度t1=0.05m,约束情况,底板四边固定铰支。
球:橡胶材料,本构关系为Moony-Rivilin,基本参数C1=3.2MPa、C2=0.8MPa、C3=0。密度ρ=1500kg/m3,厚度t2=0.02m,内压P=0.4MPa;小球的几何参数,直径D=0.2m。
装配参数:小球放在底板正上方H=0.5m处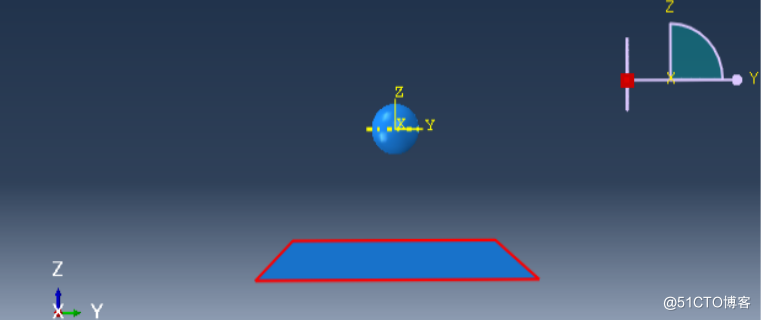
由于球是密闭容器,受到外载荷的作用后,内压随变形变化,虽然常内压无法模拟这种变化,但是由于研究变内压会使得计算更加复杂而且结果不容易收敛,因此这里采用常内压进行求解计算。这里采用ABAQUS进行建模分析。
建模步骤:
部件的创建(这一步也可以在一些CAD软件中实施):
创建部件,用三维可变形壳造底板和球,命名。
ball:3D,可变形,壳,旋转,1。轴右半圆,旋转360°。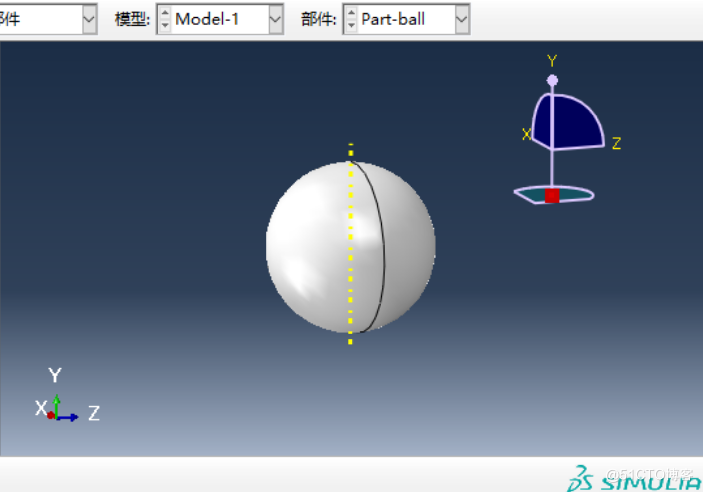
planar:3D,可变形,壳,平面,1。-0.5,-0.5; 0.5,-0.5; 0.5, 0.5; -0.5, 0.5。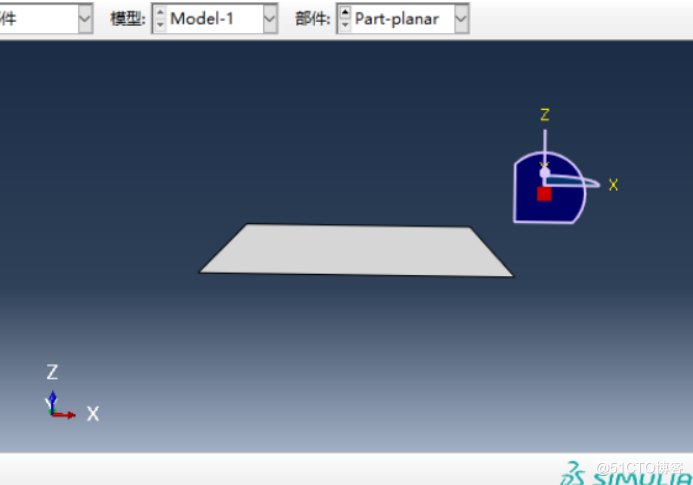
将材料命名,球的材料Material-ball:质量密度:ρ=1500kg/m3;
依次操作力学,弹性,超弹性,应变势能:Mooney-Rivlin;
输入系数:C10=3.2MPa,C01=0.8MPa,D1=0;
将材料命名,底板材料Material-planar:质量密度:ρ=2850kg/m3;
依次操作力学,弹性:弹性模量E=210GPa,泊松比v =0.28。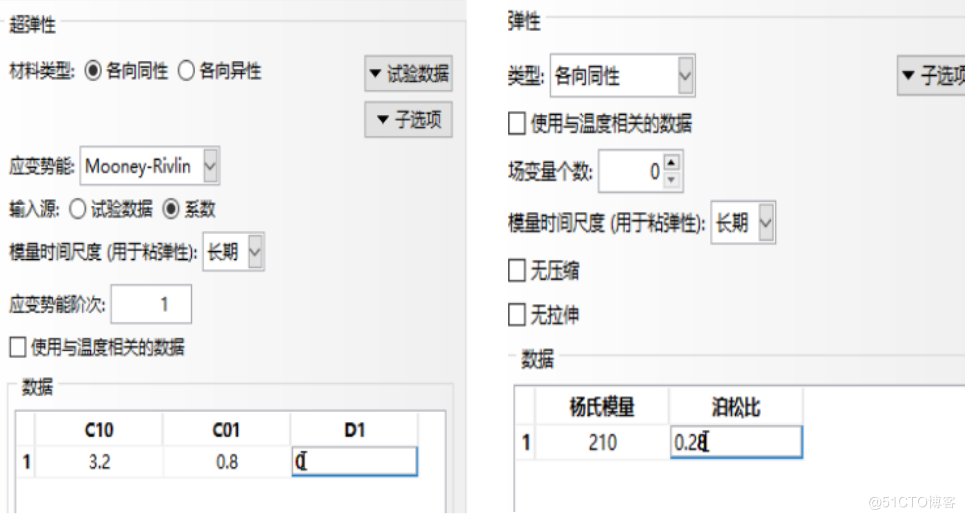
球: 命名为Section—ball。选中壳,均质;
在基本信息厚度中输入壳的厚度值:0.02;
在材料中选中之前创建的材料Material-ball。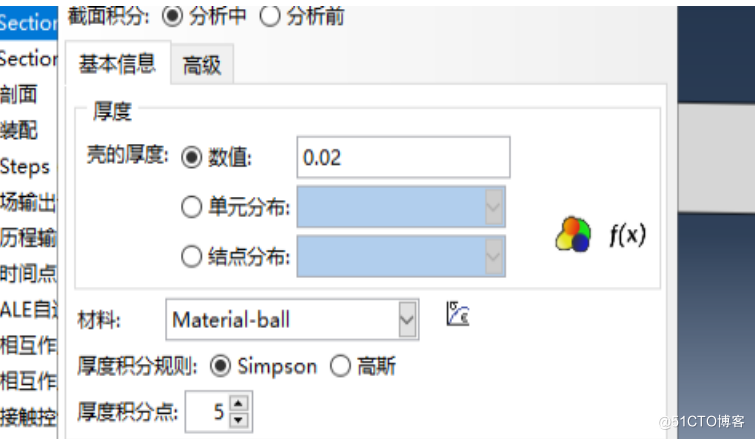
板块:命名为Section—planar。选中壳,均质;
在基本信息厚度中输入壳的厚度值:0.05;
在材料中选中之前创建的材料Material-planar。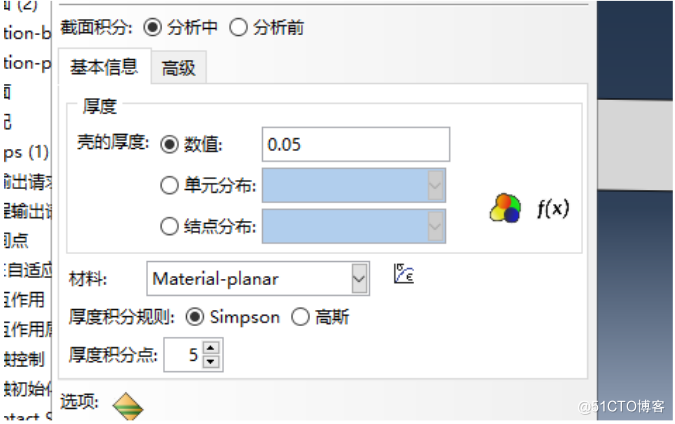
将截面的性质附加到部件上:
球:点击属性,指派截面,然后选中部件ball;在弹出的窗口中选中之前创建截面Section—ball将截面信息注入部件ball;
板块:点击属性,指派截面,然后选中部件planar;在弹出的窗口中选中之前创建截面Section—planar将截面信息注入部件planar;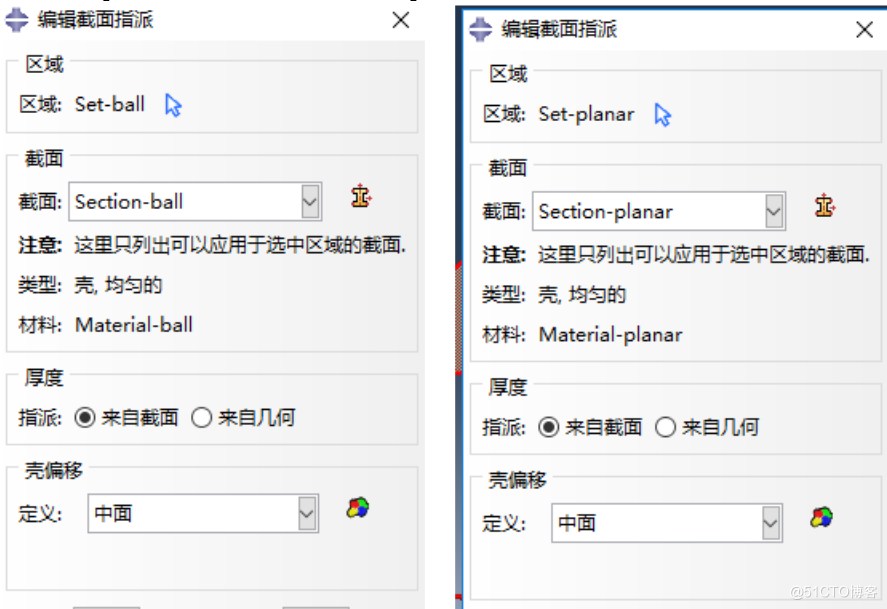
以部件ball和planar为原形,用非独立方式生成实体。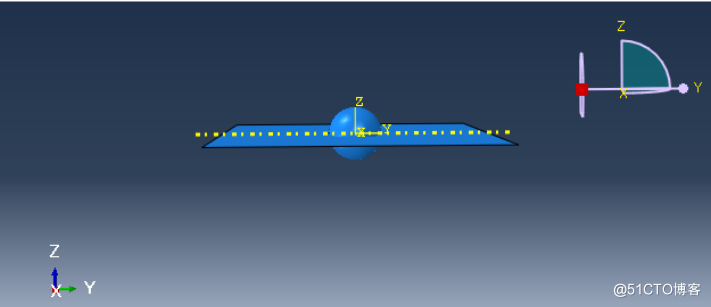
用旋转、平移等方法把底板放置到球的正下方。
创建非线性动力学分析步,命名为Step-1,动力,显式;几何非线性打开;时间长度:0.315,0~0.315s(time period 0.315);描述:The Falling Step,单击确定;
创建非线性动力学分析步,命名为Step-2,动力,显式;几何非线性打开;时间长度:0.015,0.315~0.33s(time period 0.015),描述:The Crash Step,单击确定。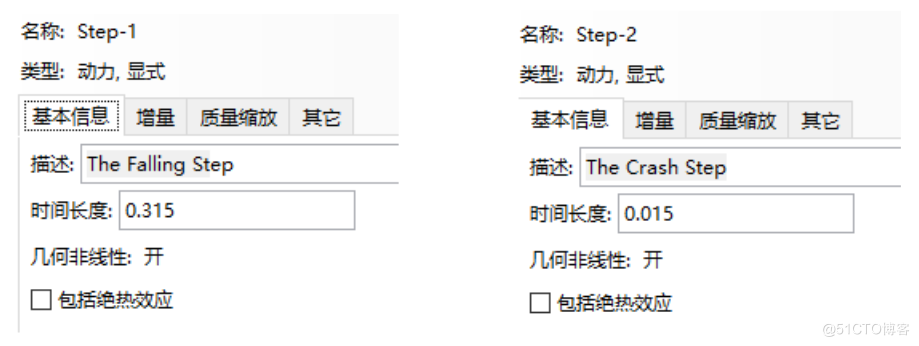
创建相互作用属性:
命名IntProp-1,属性为接触,性质:无(无摩擦有限滑动),单击Ok确定。
创建接触对:
创建轮轴接触对,创建相互作用命名int—1在初始步Step-1 中,表面与表面接触,主动面选球外表面,被动面选底板上表面。
施加位移边界条件: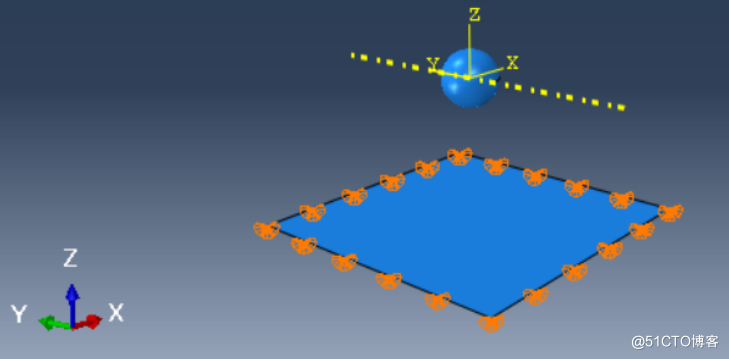
创建时间历程:
历程1:平滑历程,0s:0 幅度;0.1s:1 幅度;1.0s:1 幅度;
顶部下拉菜单,工具,幅值,创建,Amp-1,平滑分析步,0,0,0.1,1,1,1。
历程2:突变历程,0s:1 幅度;1.0s:1 幅度;
顶部下拉菜单,工具,幅值,创建,Amp-2,平滑分析步,0,1,1,1。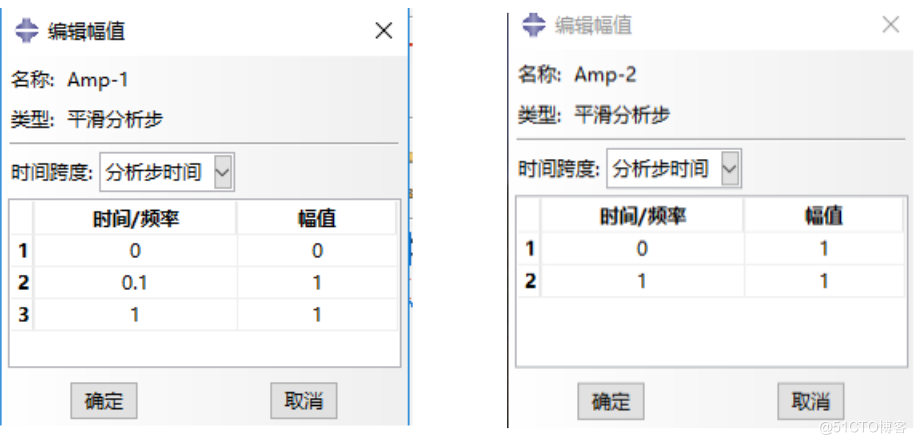
添加载荷Load—1,选择Step—1,力学,重力载荷;Z方向分量:-9.8,幅值:Amp-1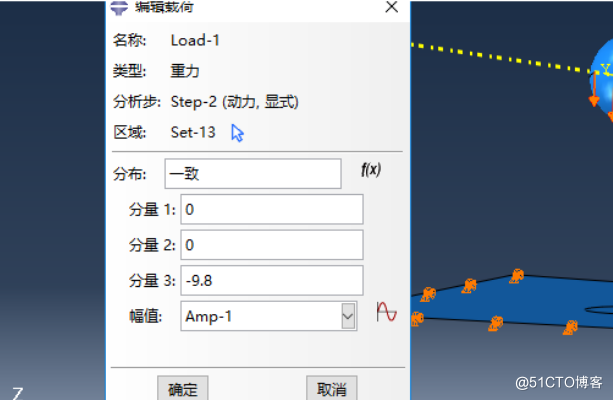
添加载荷Load—2,选择Step—2,力学,压强;大小:0.4MPa;幅值:Amp-2。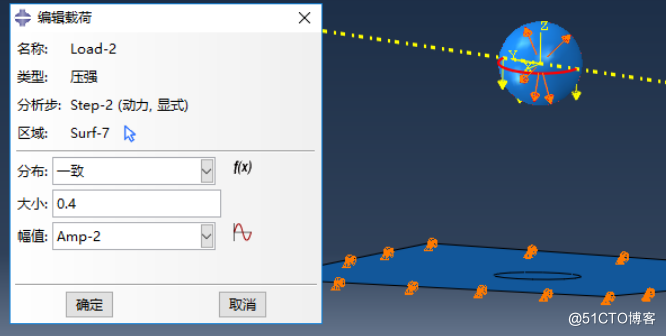
对板进行分割:将中央接触区单分区,顶部菜单工具,分区,面,草图,选中板右边界,进入草绘界面。坐标原点做一个半径为0.1m的圆;
撒种子:布种,边,选中底板四个边界,控制种子数5,选中圆,控制种子数10;
划分网格:选中部件planar,划分网格。
撒种子:顶部菜单,布种,边,选中部件ball母线,控制种子数为12;
网格控制:顶部菜单,网格,控制属性,四边形,自由;
划分网格:选中部件ball,划分网格。
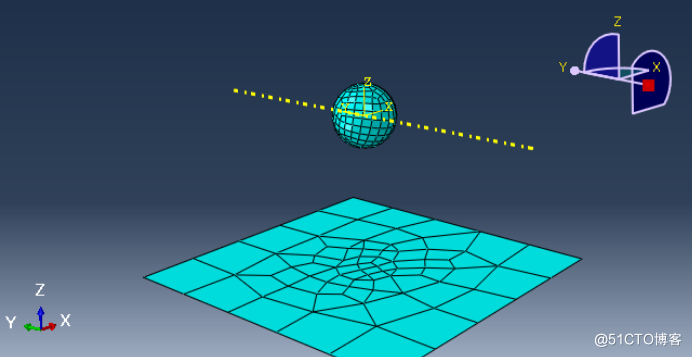
进入Job模块,创建项目求解。
项目:顶部菜单,Job,Create,命名Job—1完全分析,OK确定。
计算:进入项目管理器,作业,管理器,提交,打开Monitor查看器观看计算过程,知道计算结束。单击Results按钮进入后处理模块,查看结果。
观察结果
利用可视化后处理模块,观察小球在下落及碰撞整个过程的应力云图及动态画面。查看接触后各帧结果的应力、位移云图以及能量变化图,分析结果数据,得到问题的结论。
由于帧数有点多,这里只显示Step2中的几帧。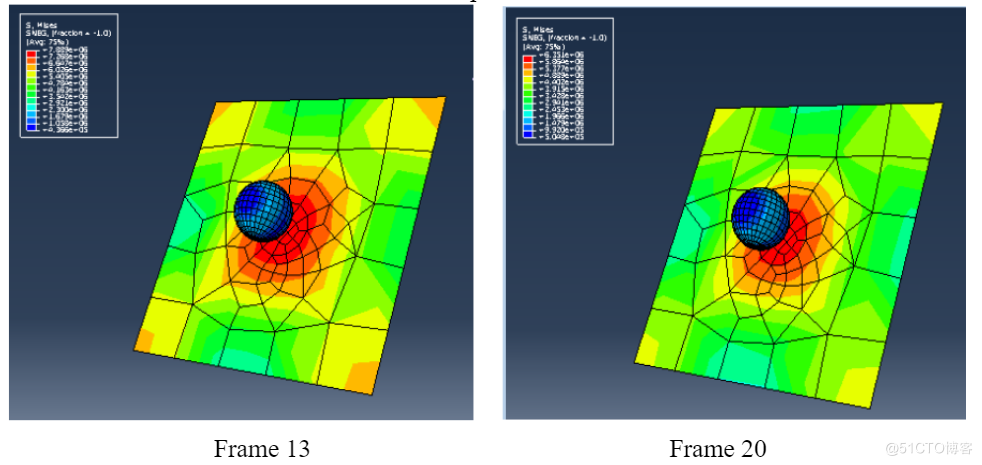
第二载荷步中小球模型中304号结点应力结果如下图所示: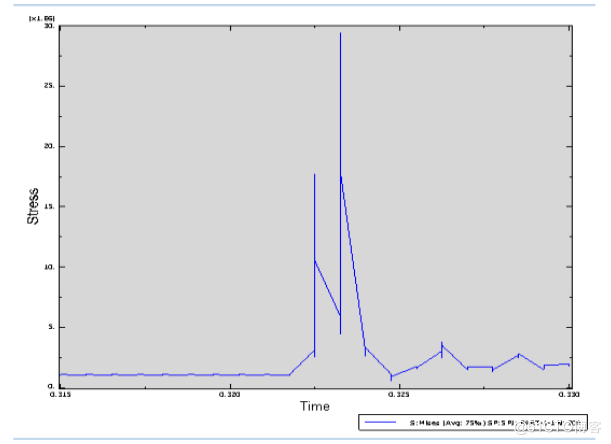
从该结果中可看出小球在0.322502秒之前应力值是趋于稳定阶段,可能这个阶段变形趋于稳定,应力变化不大;而过了该阶段,也就是0.3222502(s)—0.324751(s)阶段,小球接触区该结点应力变化幅度较大,最大可达到2.94507E+007Pa,可能在该阶段小球变形完全,也是自己弹性势能最大点。之后从0.324751秒之后直到结束,小球逐渐离开碰撞区,内力变化逐渐稳定,但由于弹性因素,还略有波动。
平板中间接触区某结点(80号)在Step2时应力结果
该课题所研究的是被撞底板在受到碰撞后板中的应力情况,这里只研究直接碰撞去某一结点的应力情况,研究该点最大值和应力变化情况。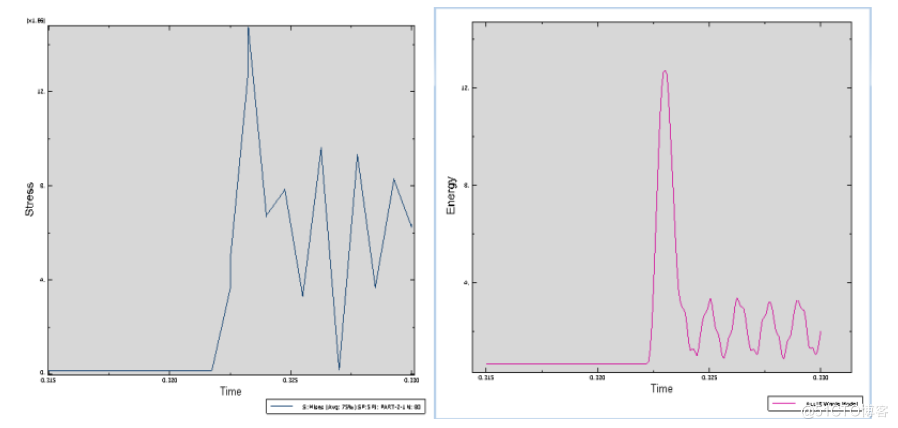
模型在整个过程的应变能变化过程如右图所示,从图中可看出,整个过程中应变能总体上是成递减状态,这也证实了碰撞能量的理论。
原文:https://blog.51cto.com/u_15145144/2726689