响应变量空间(目标变量空间)是由我们感兴趣的(或者说我们想要预测的)的变量所张成的空间。我们用\(S_Y\)来表示,m维的响应空间如下所示。
通过研究响应空间, 常把机器学习问题分为回归问题(regression)和分类问题(classification)。对于回归问题,Y常常是个数值变量,而对于分类问题,Y常常可以看成一个标签变量。
特征空间是由我们收集到的各种属性的数据所构成,如在预测身高问题中收集到的性别,父母身高等等数据。我们用\(S_X\)来表示特征空间。注意我们的问题也往往是通过收集到的特征空间的数据来预测其对应的目标空间,即我们感兴趣的变量。n维的特征空间如下,
注意的是特征空间不一定是最后我们用到的变量空间,在数据处理过程中我们需要做一定的信息提取和特征变换。这个过程是找到能够保留足够信息的最小子空间和将原空间通过映射投影到一个更合适的特征空间中(PCA,FA的思想)。我们可以用H来表示这个映射。所以我们可以得到如下的形式,
更直观的看的话,我们数据建模的过程也是研究特征空间到目标变量空间的映射。
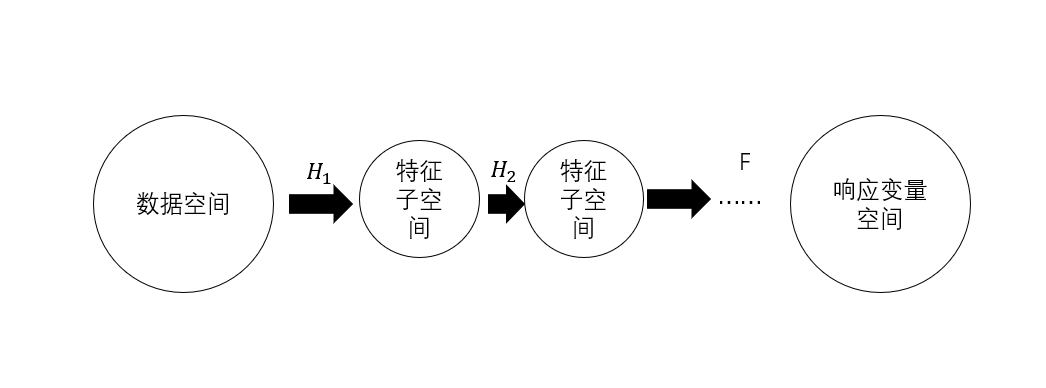
在特征空间上我们可以做的学问有很多,比如决策树方法将特征空间划分为一个一个的小块儿的特征子空间,然后在子空间上建立简单的模型;再比如主成分分析法通过对原特征空间做线性变换,获得相互正交的新的特征空间等等。
这个空间其实就是我们的研究对象,我们在已知响应空间和特征空间数据的情况下,问题往往就转化为了对参数空间的估计。值得注意的是,无论频率学派还是贝叶斯学派,其实都是在这个空间上做文章。当然这个空间不是绝对的,它还会包含超参构成的空间等。对于这个空间,我们由\(\Theta\)来表示。
注意:参数空间不一定存在,也有一些非参数的估计方法
模型空间就是可以运用到数据上的所有模型的一个集合。针对不同的问题,我们也会选择对应的不同的模型。要明确的是,我们建立模型的目的是通过特征空间和参数空间的作用来预测响应空间。换句话说,我们需要找到一个参数空间(投影矩阵)来通过特征空间来预测对应的响应空间。
建立了模型之后,最重要的是我们对参数进行估计。那么如何来估计一个参数呢?我们需要定义一个分数函数(score)来衡量一个参数的好坏,而我们的目标就是在参数满足一系列限制条件的情况下(往往是为了防止过拟合,会对参数有一定的限制)找到最好的那个参数,这样这个问题便转化成了一个最优化的问题。那么常见的评价方式有最小二乘、最大似然等等(值得注意的是,最小二乘是在高斯分布假设下的最大似然估计,两者具有一定的相通性),下面是该优化问题的一种常见的形式:
其中penalty函数常见的是向量的一范数二范数,这也是lasso regression 和 ridge regression方法的一个正则项。
对我们模型的一个客观的评价(这里有很多方法来刻画模型的好坏,如均方误差,AIC等等),从而帮助我们选择模型。下面是常见的均方误差(MSE);
AIC会将模型的复杂度也加入到我们的考虑中,这里就不做具体的分析了,我们需要知道的是针对不同的模型,我们可以建立不同的模型评估方法,分类问题有分类问题的评估方法,回归问题有回归问题的评估方法,我们要做的就是尽可能全面,系统,客观,准确的评价我们的模型,由此我们才能够客观地选择合适地模型来解决我们地问题。
我们可以将整个过程用SMOE来表示,其中S(space)是我们的数据空间,在这里,我们常常会对空间先进行一定的处理,然后对处理后的空间进行模型的建立。M(model)是模型空间,我们会尝试多种模型来探究参数空间(特征空间和响应变量空间之间的关系的刻画)。E(evaluation)是对我们模型的一个客观的评价(这里有很多方法来刻画模型的好坏,如均方误差,AIC等等),从而帮助我们选择模型。
原文:https://www.cnblogs.com/DS-blog-HWH/p/14696127.html