难度 hard
给你一个点数组 points 和一个表示角度的整数 angle ,你的位置是 location ,其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。
最开始,你面向东方进行观测。你 不能 进行移动改变位置,但可以通过 自转 调整观测角度。换句话说,posx 和 posy 不能改变。你的视野范围的角度用 angle 表示, 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数,那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。
对于每个点,如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ,那么你就可以看到它。
同一个坐标上可以有多个点。你所在的位置也可能存在一些点,但不管你的怎么旋转,总是可以看到这些点。同时,点不会阻碍你看到其他点。
返回你能看到的点的最大数目。
示例 1:
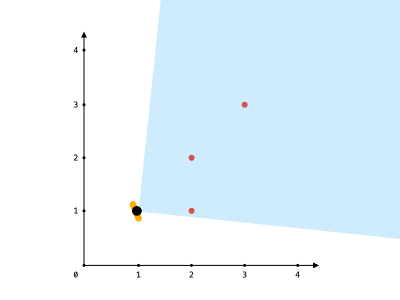
输入:points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出:3
解释:阴影区域代表你的视野。在你的视野中,所有的点都清晰可见,尽管 [2,2] 和 [3,3]在同一条直线上,你仍然可以看到 [3,3] 。
示例 2:
输入:points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出:4
解释:在你的视野中,所有的点都清晰可见,包括你所在位置的那个点。
示例 3:
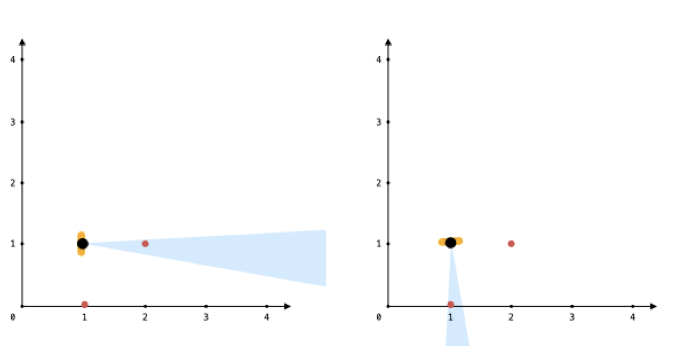
输入:points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出:1
解释:如图所示,你只能看到两点之一。
提示:
1 <= points.length <= 105
points[i].length == 2
location.length == 2
0 <= angle < 360
0 <= posx, posy, xi, yi <= 100
解题思路:这道题目其实也算是相对来说常规的,只是要用到一些技巧,一个是Math.atan2这个函数,可以根据点坐标计算出角度,自动分好象限,最后就只出现在[-pi/2,pi/2]这个区间里面,这样我们讨论起来就非常方便了,然后有一个特殊的情况,就是我们找到的点是location本身,这种情况下atan2不好处理,因此我们把它单独计数,最后就是我们要做到不漏掉角度差计算上大于阈值但实际上单位圆上的角度差小于阈值呢?解决方法就是多循环一次。由于圆的角度是2pi弧度,因此我们需要同时加入两个角度,一个是 atan2 的结果,一个是 atan2 + 2pi 的结果,这样就能保证不会漏掉了。
代码 t15 s60 java
class Solution {
public int visiblePoints(List<List<Integer>> points, int angle, List<Integer> location) {
List<Double> angles = new ArrayList<>();
int ansExr = 0;
for(int i=0; i<points.size(); i++){
int delta_y = points.get(i).get(1) - location.get(1);
int delta_x = points.get(i).get(0) - location.get(0);
if(delta_y==0 && delta_x==0){
ansExr++;
continue;
}
angles.add(Math.atan2(delta_y, delta_x));
angles.add(Math.atan2(delta_y, delta_x) + 2 * Math.PI);
}
Collections.sort(angles);
double angle_radians = Math.toRadians(angle);
int left = 0, right = 0, res = 0;
while(true){
if(right==angles.size()){
break;
}else if(angles.get(right)-angles.get(left)<=angle_radians){
res = Math.max(res, right - left + 1);
right++;
}else{
left++;
}
}
return res + ansExr;
}
}
原文:https://www.cnblogs.com/zhengxch/p/14696904.html