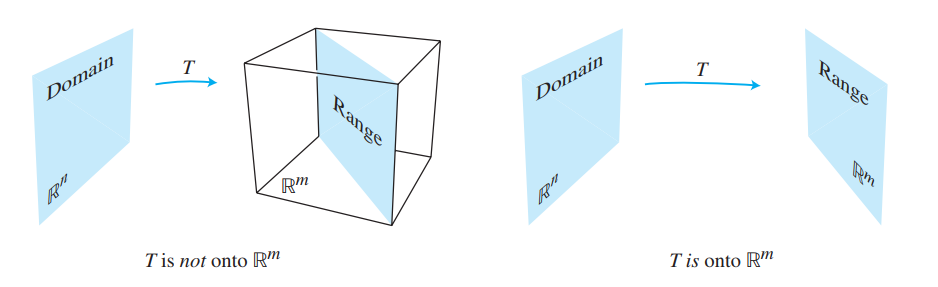
满射(onto) 和 单射(one-to-one)

1. 满射
   A mapping \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be onto \(\mathbb{R}^{m}\) if each \(\mathbf{b}\) in \(\mathbb{R}^{m}\) is the image of at least one \(\mathbf{x}\) in \(\mathbb{R}^{n}\).
   

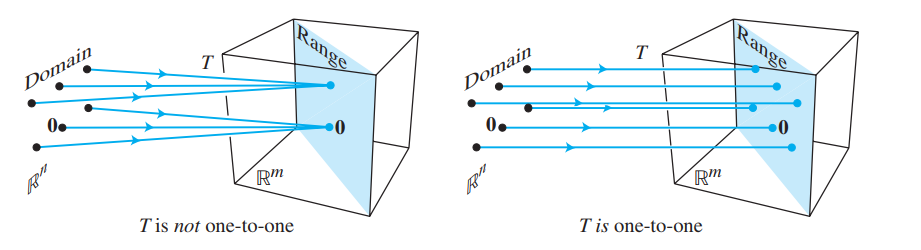
2. 单射
   A mapping \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be one-to-one if each \(\mathbf{b}\) in \(\mathbb{R}^{m}\) is the image of at most one \(\mathbf{x}\) in \(\mathbb{R}^{n}\).

满射(onto) 和 单射(one-to-one)

原文：https://www.cnblogs.com/Noame/p/14696495.html