二叉排序树（C语言，又称二叉查找树）

? 节点的data必须是能标识一个独立树节点的主关键字

? 中序遍历后的序列是从小到大

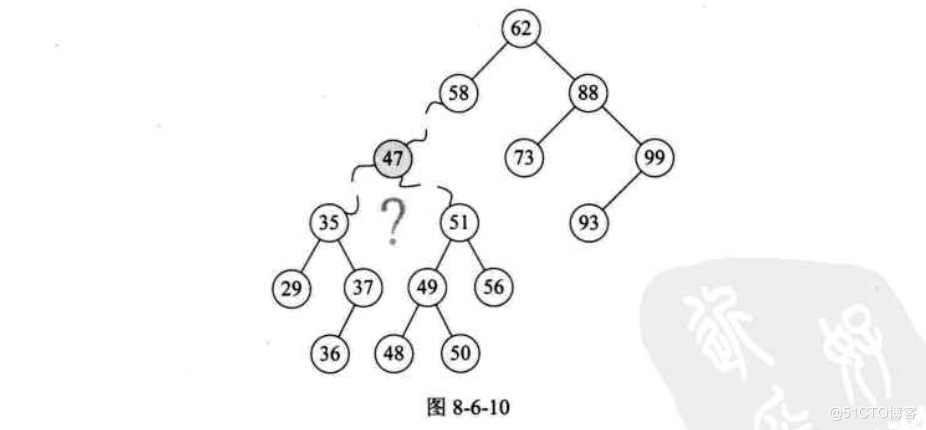
图来源：

? 《大话数据结构》p321 图8-6-10

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct TNode {
    int data;
    struct TNode *lchild, *rchild;
}TNode, *Tree;

bool search(Tree, int, Tree, Tree *);
bool insert(Tree *, int);
void traverse_mid(Tree);
bool delete_bst(Tree *, int);
bool delete(Tree *);

bool delete(Tree *pT)
{
    /*删除比较复杂，分3大类情况:
     *    *pT无右子树（左子树可能为空，也可能存在，*pT可能为根节点）
     *    *pT无左子树（右子树可能为空，也可能存在，*pT可能为根节点）
     *    *pT 同时有左子树和右子树
     *下面的注释中的前驱都是指中序遍历的前驱
     */     
    Tree q, s;

    if (! (*pT)->rchild) {
        printf("del %d, 无rchild, lchild: %d\n", (*pT)->data, (*pT)->lchild?(*pT)->lchild->data:0);
        q = *pT; 
        *pT = (*pT)->lchild; // 连接自身左子树
        free(q);
    }
    else if (! (*pT)->lchild) {
        printf("del %d, 无lchild, rchild: %d\n", (*pT)->data, (*pT)->rchild?(*pT)->rchild->data:0);
        q = *pT;
        *pT = (*pT)->rchild; // 连接自身右子树
        free(q);
    }
    else {
        printf("del %d, lchild: %d, rchild: %d\n", (*pT)->data, (*pT)->lchild->data, (*pT)->rchild->data);
        q = *pT;
        s = (*pT)->lchild;
        // 这个循环目的是找出其最大的子孙节点s
        while (s->rchild) {
            q = s;
            s = s->rchild;
        }

        /* 与前两种情况不同，这里并没有释放被删节点的内存地址
         * 只是把找到的接替自己位置的节点（左子树最大值，另外也可以用右子树最小值算法）
         * 找到的替身节点最后被释放
         */
        (*pT)->data = s->data;
        if (q == *pT)
            // while没有执行，表示s已经是最大值(其左子树可能存在也可能为空，直接连接左子树)
            q->lchild = s->lchild;
        else
            // while执行了，把s的左孩子连接到s的前驱q
            q->rchild = s->lchild;
        free(s);
    }
        return true;
}
// 之所以需要Tree *同样是考虑到了根节点
bool delete_bst(Tree *pT, int key)
{
    if (! (*pT))
        return false;

    if (key == (*pT)->data)
        return delete(pT);
    else if (key < (*pT)->data)
        return delete_bst(&(*pT)->lchild, key);
    else
        return delete_bst(&(*pT)->rchild, key);
}

void traverse_mid(Tree T)
{
    if (!T)
        return;
    traverse_mid(T->lchild);
    printf("%d ", T->data);
    traverse_mid(T->rchild);
}

bool insert(Tree *pT, int key)
{
    Tree p, pNew;

    pNew = (Tree)malloc(sizeof(TNode));
    pNew->data = key;
    pNew->lchild = pNew->rchild = NULL;

    if (! search(*pT, key, NULL, &p)) {
        if (! p) { // *pT本就是一个空树，即本次插入的节点为T的根节点
            printf("插入根节点: %d\n", pNew->data);
            *pT = pNew; // 本函数之所以用Tree *类型就是因为存在这种情况
        }
        else if (key < p->data) {
            // 作为左孩子插入
            printf("插入 %d 的lchild %d\n", p->data, pNew->data);
            p->lchild = pNew;
        }
        else {
            // 作为右孩子插入
            printf("插入 %d 的rchild %d\n", p->data, pNew->data);
            p->rchild = pNew;
        }
        return true;
    }
    else {
        return false;
    }

}

/* 第3个参数f，在插入节点的时候起作用，如果只是确认元素是否存在其实不用后面的f和*p参数
 */ 
bool search(Tree T, int key, Tree f, Tree *p)
{
    /* f的值有3种情况：
     *    首次运行时T就为假(查找空树)，则f为调用时传入的NULL
     *    查找过程中递归到了尽头未找到，则f为最后一个遍历的节点(作为将来添加节点的父节点);
     *    真正找到了匹配的节点, f为此节点
     */
    if (! T) {
        *p = f;
        return false;
    }

    if (key == T->data) {
        *p = T;
        return true;
    }
    else if (key < T->data)
        // 递归查左孩子，第3个参数传入自身，当左孩子为NULL时，T会赋值给*p
        return search(T->lchild, key, T, p);
    else 
        // 递归查右孩子，第3个参数传入自身，当右孩子为NULL时，T会赋值给*p
        return search(T->rchild, key, T, p);

}

int main(void)
{
    Tree tree;
    insert(&tree, 62);
    insert(&tree, 58);
    insert(&tree, 88);
    insert(&tree, 47);
    insert(&tree, 73);
    insert(&tree, 99);
    insert(&tree, 35);
    insert(&tree, 51);
    insert(&tree, 93);
    insert(&tree, 29);
    insert(&tree, 37);
    insert(&tree, 49);
    insert(&tree, 56);
    insert(&tree, 36);
    insert(&tree, 48);
    insert(&tree, 50);
    traverse_mid(tree); putchar(‘\n‘);

    delete_bst(&tree, 29);
    traverse_mid(tree); putchar(‘\n‘);
    delete_bst(&tree, 99);
    traverse_mid(tree); putchar(‘\n‘);
    delete_bst(&tree, 47);
    traverse_mid(tree); putchar(‘\n‘);

    return 0;
}

output

[root@8be225462e66 c]# gcc search_tree.c && ./a.out
插入根节点: 62
插入 62 的lchild 58
插入 62 的rchild 88
插入 58 的lchild 47
插入 88 的lchild 73
插入 88 的rchild 99
插入 47 的lchild 35
插入 47 的rchild 51
插入 99 的lchild 93
插入 35 的lchild 29
插入 35 的rchild 37
插入 51 的lchild 49
插入 51 的rchild 56
插入 37 的lchild 36
插入 49 的lchild 48
插入 49 的rchild 50
29 35 36 37 47 48 49 50 51 56 58 62 73 88 93 99
del 29, 无rchild, lchild: 0
35 36 37 47 48 49 50 51 56 58 62 73 88 93 99
del 99, 无rchild, lchild: 93
35 36 37 47 48 49 50 51 56 58 62 73 88 93
del 47, lchild: 35, rchild: 51
35 36 37 48 49 50 51 56 58 62 73 88 93
[root@8be225462e66 c]#

二叉排序树（C语言，又称二叉查找树）

原文：https://blog.51cto.com/sndapk/2731839