编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例 :
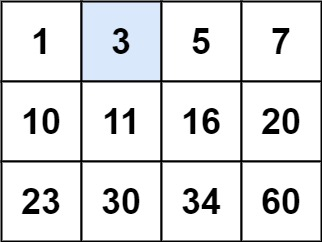
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
这个题主要在于观察一下规律,如果从右上角顶点开始,那么满足:小于往左走,大于往下走,就像一颗二叉树,因此二分查找,比暴力法更优。
class Solution { public boolean searchMatrix(int[][] matrix, int target) { int height = matrix.length; int length = matrix[0].length; //二分查找,从matrix[0][length-1] 开始,大于当前值则往下走,反之往左走。 int down = 0, left = length-1; while (down<height && left>=0){ if(matrix[down][left]==target){ return true; } if(matrix[down][left]>target){ left--; }else { down++; } } return false; } }
时间复杂度:O(log(m*n)),空间复杂度:O(1)
原文:https://www.cnblogs.com/daxiaq/p/14700667.html