两道有序二维矩阵算法

题目：第K小元素

解法：

充分利用有序性可以使用二分，如果我们有一个target 二维矩阵必然存在一条曲线从左下到右上可以把矩阵分为两部分，如果小于target的数小于等于k，说明target比目标值大。

为什么我们能保证最终返回的值一定在矩阵中呢，假如矩阵中小于等于[7,10)的数目为k，显然我们二分时让r=mid，会不断寻找出最左边的满足条件的值即7

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
      int n=matrix.length-1; 
      int left=matrix[0][0];
      int right=matrix[n][n];
      int mid;
      while(left<right){
         mid=(right+left)>>1;
         if(check(matrix,mid,k)){
             right=mid;
         }else{
             left=mid+1;
         }
      }
      return right;
    }
    public boolean check(int[][] matrix,int mid,int k){
        int n=matrix.length-1;
        int row=n;
        int col=0;
        int num=0;
        while(row>=0&&col<=n){
            if(matrix[row][col]<=mid){
               num=num+row+1;
               col++;
            }else{
                row--;
            }
        }
        return num>=k;
    }
}

题目：搜索二维矩阵

解法：

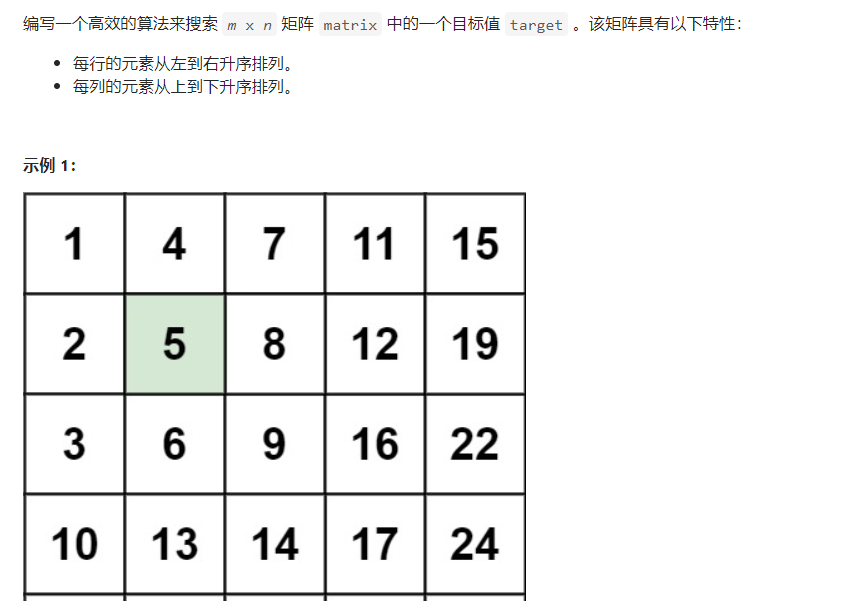
我们可以从左下开始搜索，原因是可以分为两个方向,>target就往上找，<target就往右找，同理从右上也可以

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int  row=matrix.length-1;
        int  col=0;
        while(row>=0 && col<matrix[0].length){
            if(matrix[row][col]==target){
                return true;
            }
            if(matrix[row][col]>target){
                row--;
            }else {
                col++;
            }
        }
        return false;
        
    }
}

两道有序二维矩阵算法

原文：https://www.cnblogs.com/wangstudyblog/p/14702235.html