hdu5035：概率论推公式

题目大意：

你要去邮局发一个包裹，有n个窗口，每个都有人，每一个窗口完成一次服务的时间 ti 的分布符合几何分布：ki*e^(-ki*t)

每个窗口当前服务已经进行了ci时间

你会去第一个完成当前服务的窗口，求你从到达邮局到寄完包裹花费总时间的期望

据说是概率论书上的题目。。概率论才学了一章的哭瞎

比赛的时候题还没完全都清楚，感觉概率应该用积分算，就开始积分，最后搞了半天也是不了了知

后来看了大牛的题解，总算看懂了，也自己推了∫+∞xf(x:λj)dx一次。。

思路：

首先对单个窗口进行概率积分 ∫+∞xf(x:λj)dx ∫+∞xf(x:λj)dx∫+∞xf(x:λj)dx∫+∞xf(x:λj)dx得到完成时间在[0,t]内的概率为 1-e^(-ki*t)，所以[t,+∞]的概率即为 e^(-ki*t)；

再对期望积分 得到 E(i)=1/ki；

通过以上概率每个窗口完成当前服务的时间是和已经进行的时间ci是无关的（这个由条件概率很好算出）

所以，我们设 在第 t 时刻，你来到了 i 窗口，那么应该满足什么条件呢

根据题意，你将会去结束当前服务最早的一个窗口，所以，你去此窗口的必要条件是 ，其他窗口在 t 时刻并没有结束自己的当前工作

这个概率由乘法原理可以容易写出：

即为  ∏ (j=1...n,j!=i):e^(-kj*t) 。

而花费的时间即为 t (在当前服务上花的时间)  +  E(i) (在你身上花的时间的期望)。

由于 t 是连续的，还需要对 t 进行积分。

最后再对每一个窗口进行求和，得到期望的表达式

化简过程就需要各种积分了。。所以高数功底还是很重要的啊。

如图：

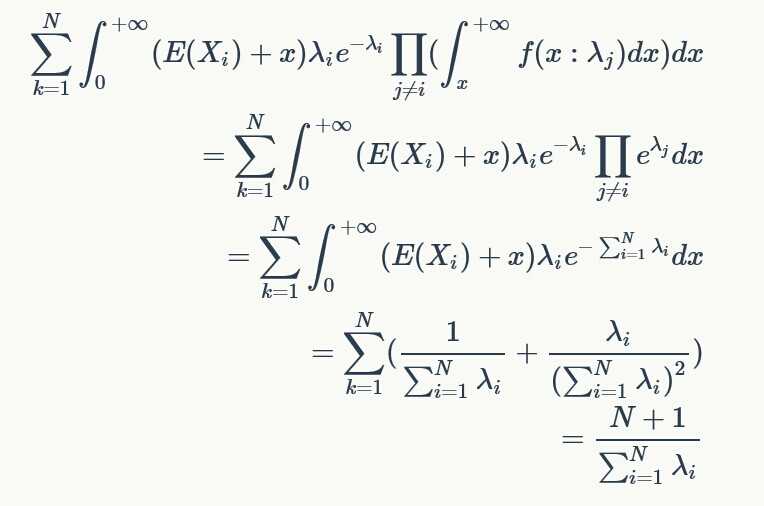
最后推出公式。。代码就好写了

#include <iostream>
#include <stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<string>
#include<ctype.h>
using namespace std;
#define MAXN 10000
double k[1010];
int main()
{

    int tt;
    scanf("%d",&tt);
    int n;
    int cas=0;
    while(tt--)
    {
        cas++;
        scanf("%d",&n);
        double ans=0;
        for(int i=0;i<n;i++)
        {
            scanf("%lf",k+i);
            ans+=k[i];
        }
        for(int i=0;i<n;i++)
        {
            scanf("%lf",&k[1000]);
        }
        printf("Case #%d: %.6f\n",cas,(n+1)/ans);
    }


    return 0;
}

hdu5035：概率论推公式

原文：http://www.cnblogs.com/oneshot/p/3985938.html