@
? 该数据集是IMDB电影数据集的一个子集,已经划分好了测试集和训练集,训练集包括25000条电影评论,测试集也有25000条,该数据集已经经过预处理,将每条评论的具体单词序列转化为词库里的整数序列,其中每个整数代表该单词在词库里的位置。例如,整数104代表该单词是词库的第104个单词。为实验简单,词库仅仅保留了10000个最常出现的单词,低频词汇被舍弃。每条评论都具有一个标签,0表示为负面评论,1表示为正面评论。
? 训练数据在train_data.txt文件下,每一行为一条评论,训练集标签在train_labels.txt文件下,每一行为一条评论的标签;测试数据在test_data.txt文件下,测试数据标签未给出。
取出数据集:
从txt中取出训练集与测试集:
with open("test/test_data.txt", "rb") as fr:
test_data_n = [inst.decode().strip().split(‘ ‘) for inst in fr.readlines()]
test_data = [[int(element) for element in line] for line in test_data_n]
test_data = np.array(test_data)
数据处理:
对每条评论,先将其解码为英文单词,再键值颠倒,将整数索引映射为单词。
把整数序列编码为二进制序列。
最后把训练集标签向量化。
# 将某条评论解码为英文单词
word_index = imdb.get_word_index() # word_index是一个将单词映射为整数索引的字典
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
# 键值颠倒,将整数索引映射为单词
decode_review = ‘ ‘.join(
[reverse_word_index.get(i - 3, ‘?‘) for i in train_data[0]]
)
\# 将评论解码
\# 注意,索引减去了3,因为0,1,2是为padding填充
\# "start sequence"序列开始,"unknow"未知词分别保留的索引
\# 将整数序列编码为二进制矩阵
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension)) # 创建一个形状为(len(sequences), dimension)的矩阵
for i, sequence in enumerate(sequences):
results[i, sequence] = 1 # 将results[i]的指定索引设为 1
return results
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
\# 标签向量化
y_train = np.asarray(train_labels).astype(‘float32‘)
建立模型:
可选多项式模型或者伯努利模型。
二者的计算粒度不一样,多项式模型以单词为粒度,伯努利模型以文件为粒度,因此二者的先验概率和类条件概率的计算方法都不同。
计算后验概率时,对于一个文档d,多项式模型中,只有在d中出现过的单词,才会参与后验概率计算,伯努利模型中,没有在d中出现,但是在全局单词表中出现的单词,也会参与计算,不过是作为“反方”参与的。
当训练集文档较短,也就说不太会出现很多重复词的时候,多项式和伯努利模型公式的分子相等,多项式分母值大于伯努利分子值,因此多项式的似然估计值会小于伯努利的似然估计值。
所以,当训练集文本较短时,我们更倾向于使用伯努利模型。而文本较长时,我们更倾向于多项式模型,因为,在一篇文档中的高频词,会使该词的似然概率值相对较大。
使用拉普拉斯平滑
alpha:先验平滑因子,默认等于1,当等于1时表示拉普拉斯平滑。
# model = MultinomialNB()
model = BernoulliNB()
model.fit(X_train, y_train)
输出测试集上的预测结果:
将结果写入txt
# model evaluation
print("model accuracy is " + str(accuracy_score(y_test, y_pred)))
print("model precision is " + str(precision_score(y_test, y_pred, average=‘macro‘)))
print("model recall is " + str(recall_score(y_test, y_pred, average=‘macro‘)))
print("model f1_score is " + str(f1_score(y_test, y_pred, average=‘macro‘)))
des = y_pred_local.astype(int)
np.savetxt(‘Text3_result.txt‘, des, fmt=‘%d‘, delimiter=‘\n‘)
使用多项式模型:
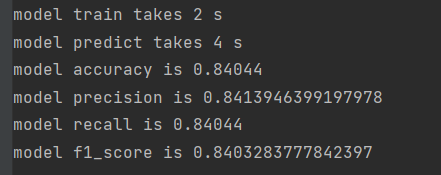
使用伯努利模型:
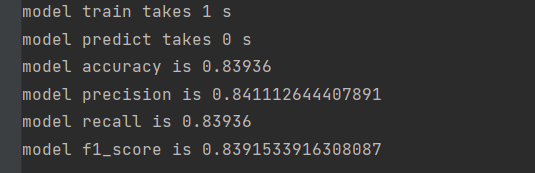
在该场景下,两者差别不大。
原文:https://www.cnblogs.com/yuetianw/p/14707599.html