文章首先于微信公众号:小K算法,关注第一时间获取更新信息
结点和边,构成一个图。
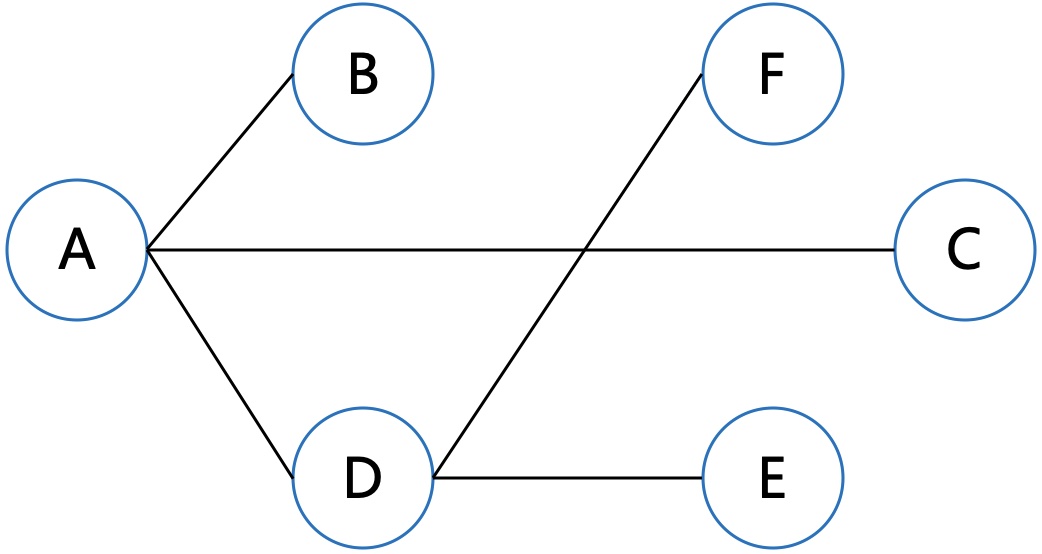
不含环的连通图,便成了一棵树。每个结点拥有的子结点数称为结点的度。
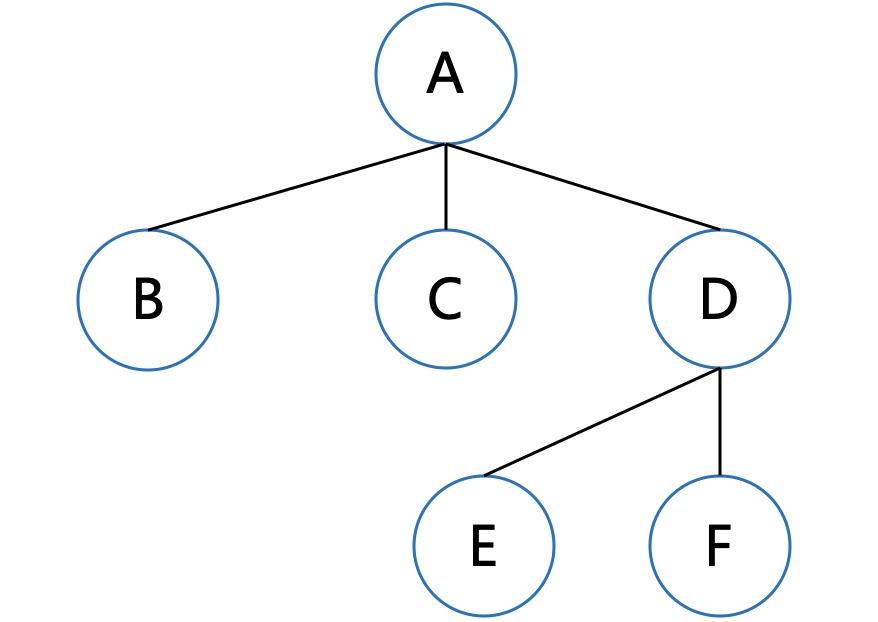
多棵树便构成了一个森林。
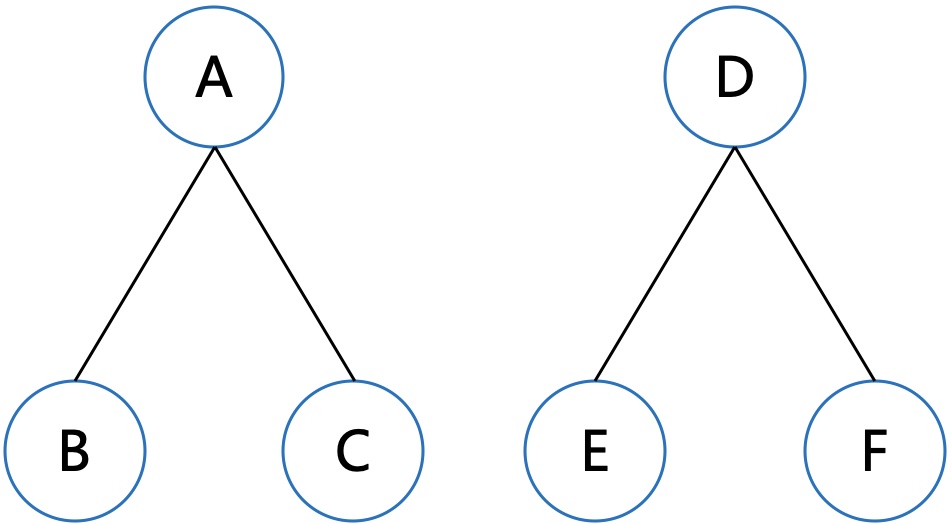
结点的度最大为2的树便是二叉树;最大度为N的是N叉树,或多叉树。
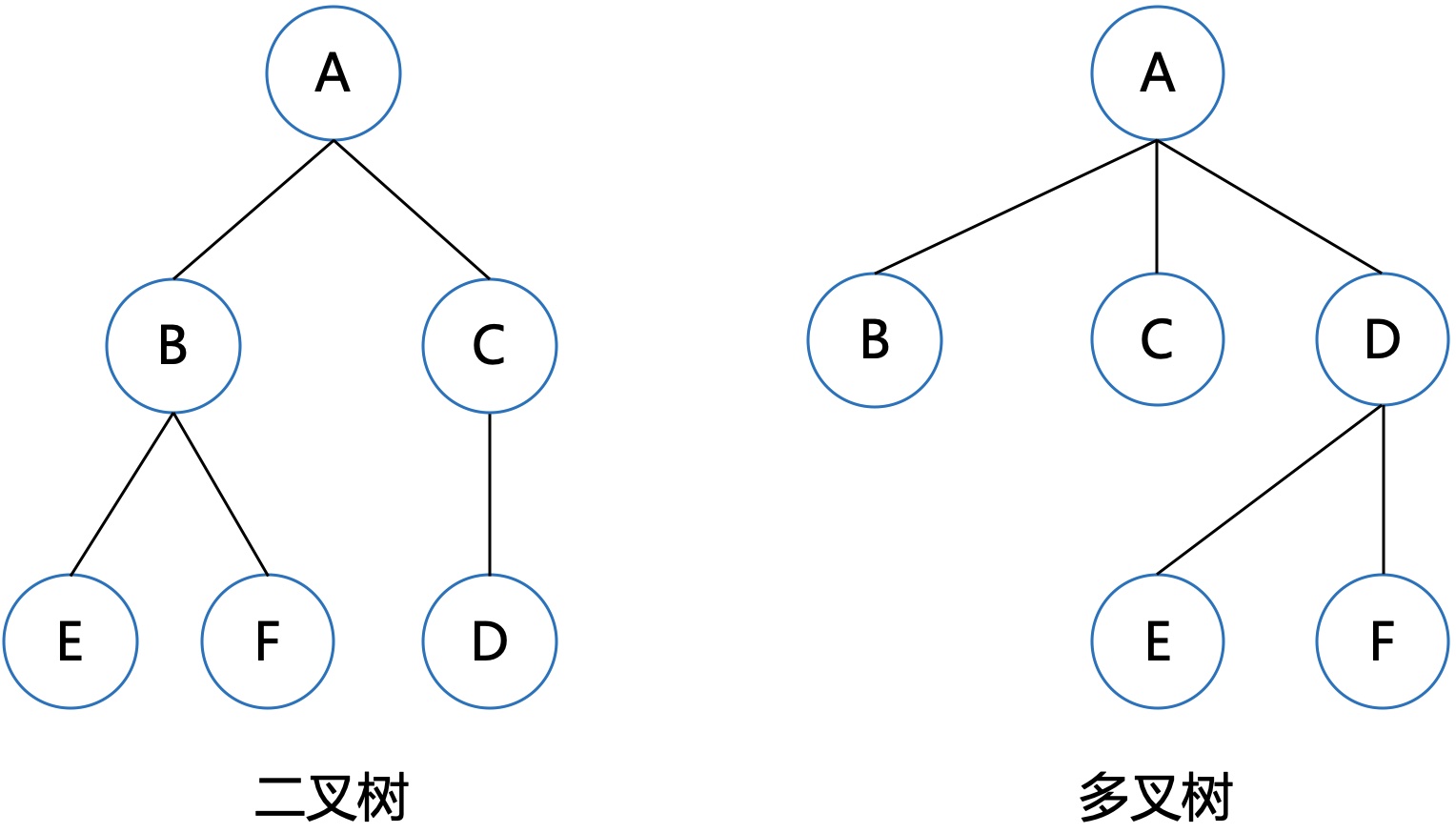
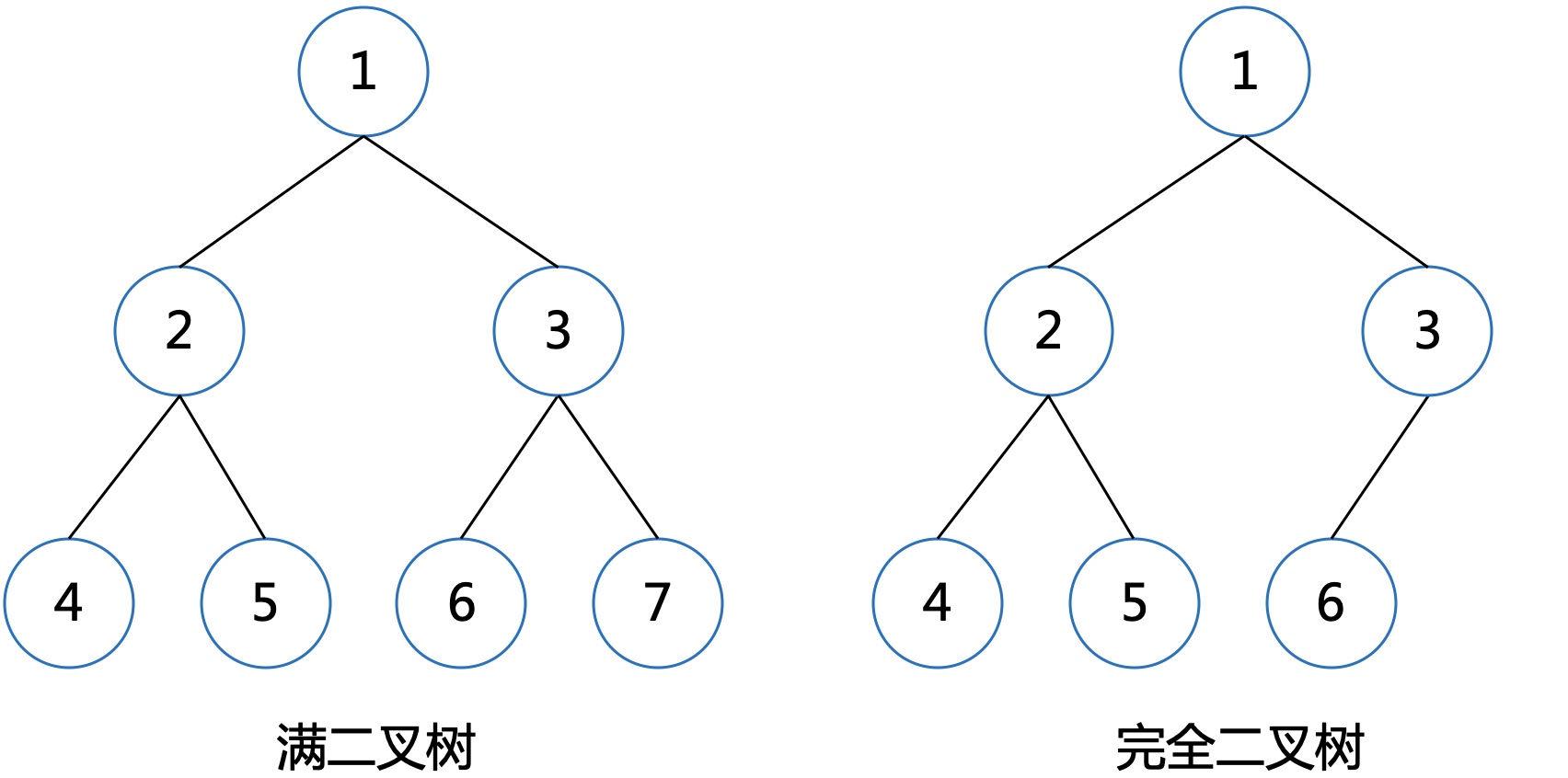
除叶子结点,每个结点的度都为2,称为满二叉树。
除去最后一层之后的子树为满二叉树,且最后一层结点依次从左到右分布,则称为完全二叉树。
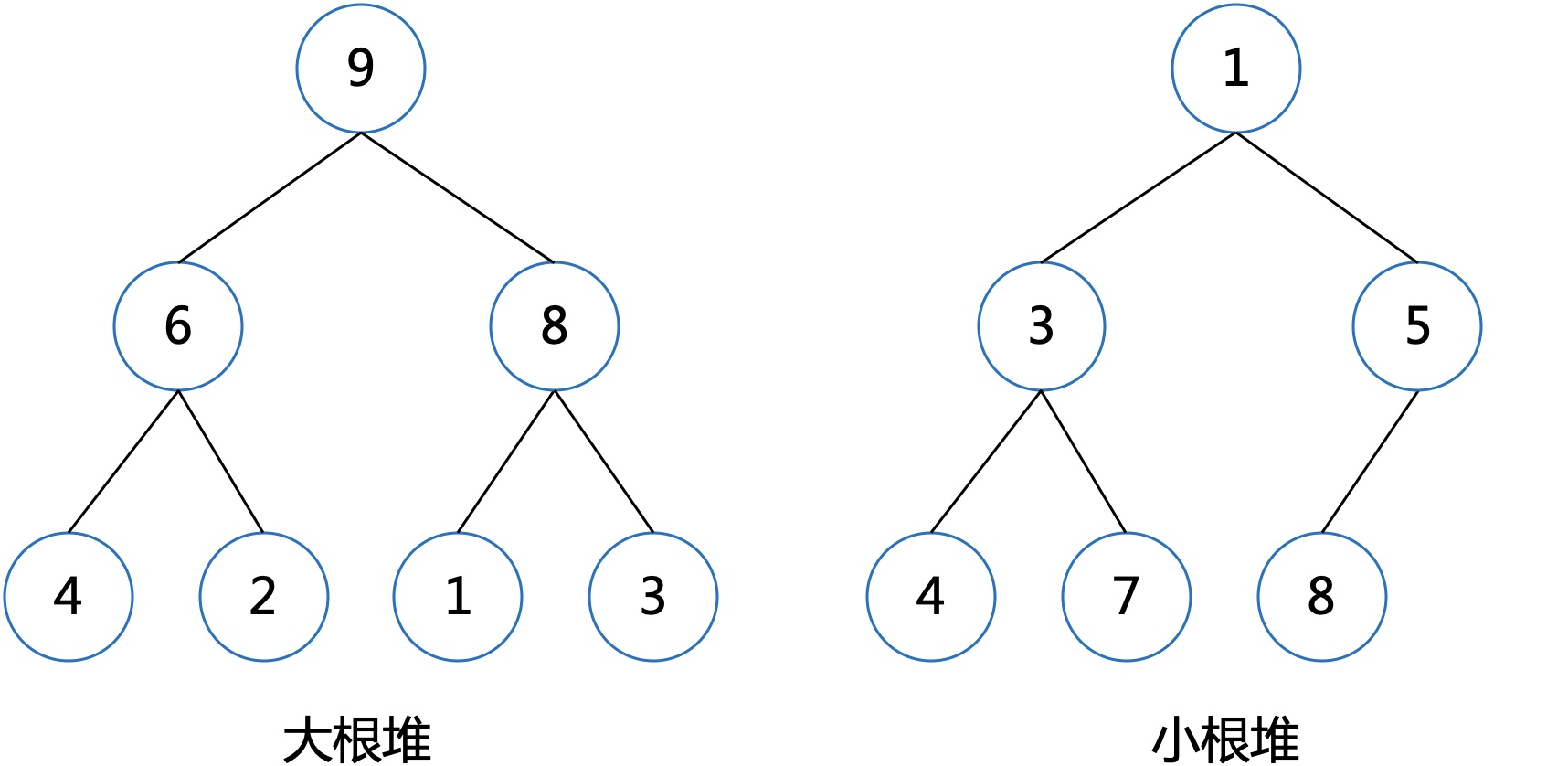
如果在完全二叉树上再加一个限制条件:如结点都大于等于其子结点,或者小于等于其子结点,则称为堆。
每个结点都大于等于其子结点,称为大根堆。
每个结点都小于等于其子结点,称为小根堆。
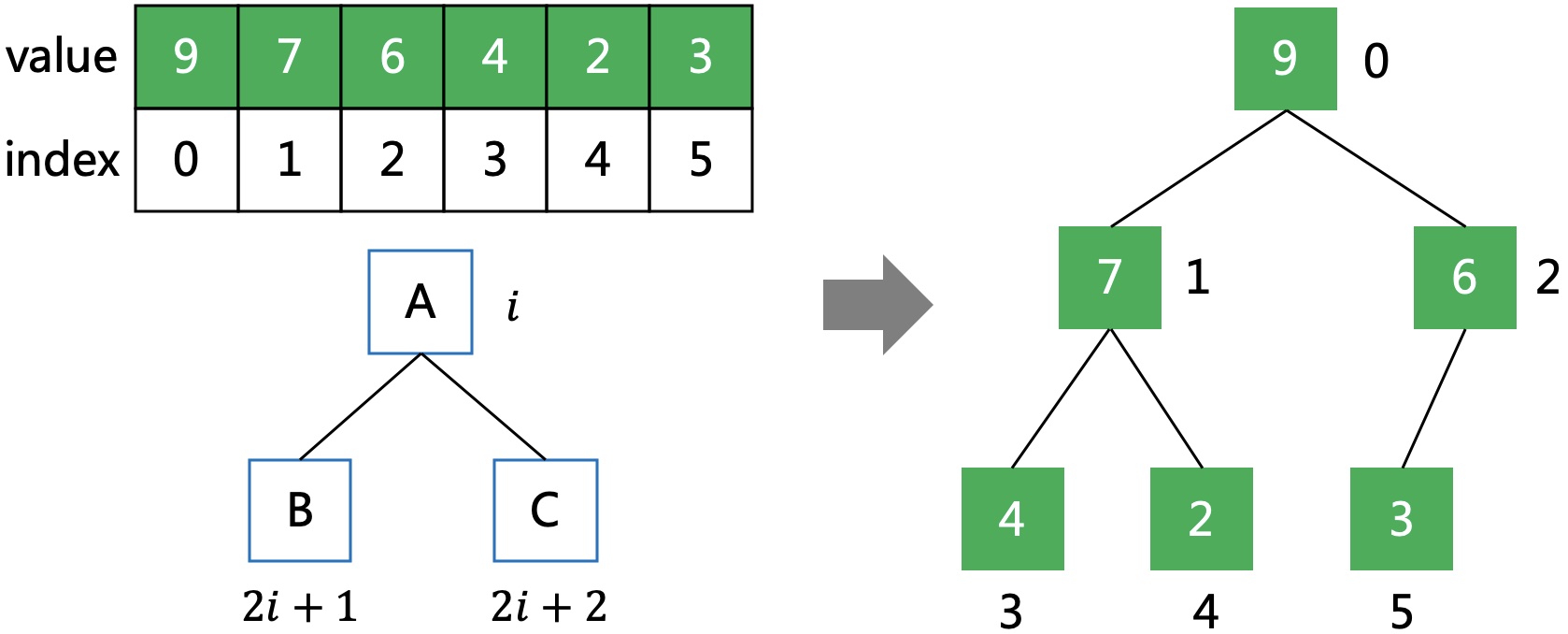
用数组存储,将一个线性数组映射成一棵完全二叉树,父结点为i,则左儿子为2i+1,右儿子为2i+2。
代码如下
int heap[10];
定义一个结点的结构体,两个指针分别指向左儿子和右儿子。
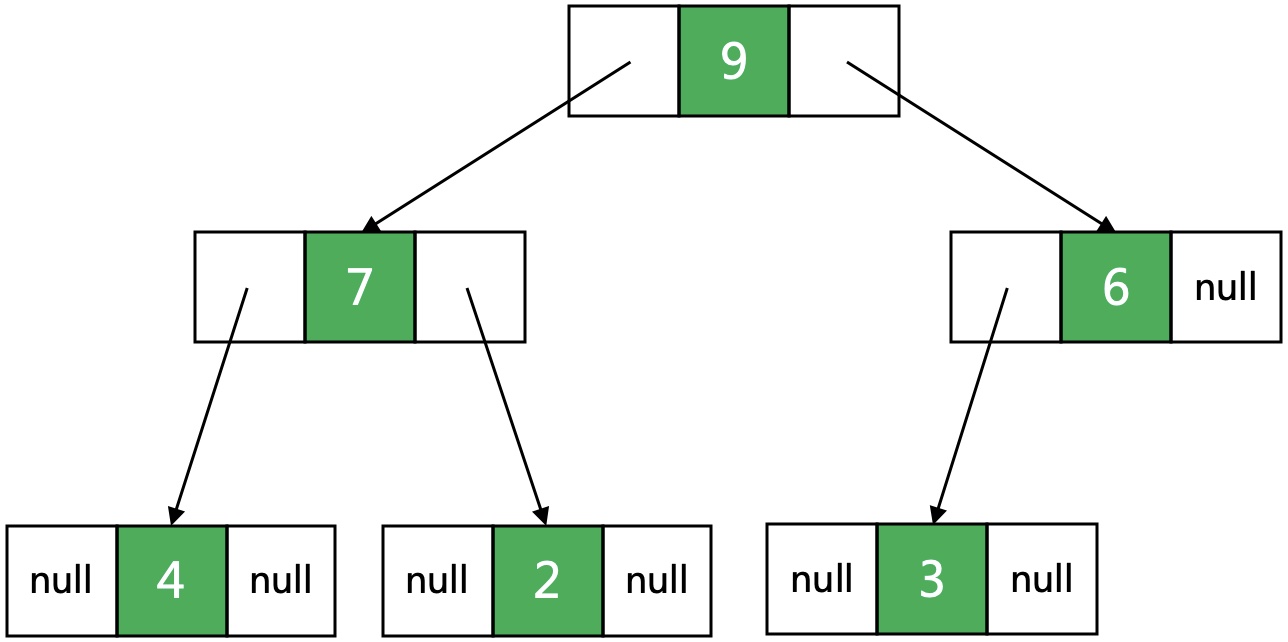
代码如下
struct Node {
int value;
Node *lson, *rson;
};
Node *heap;
以下思想都以大根堆举例。
子结点与父结点的下标关系如下:
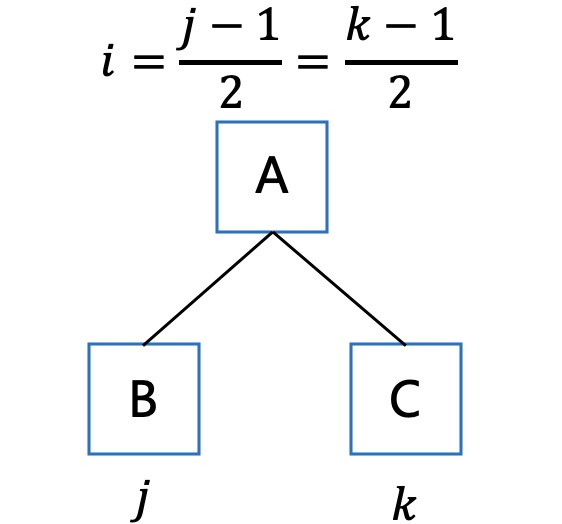
用一个指针指向待调整的结点:
直到指向根结点或者当前结点小于等于父结点。
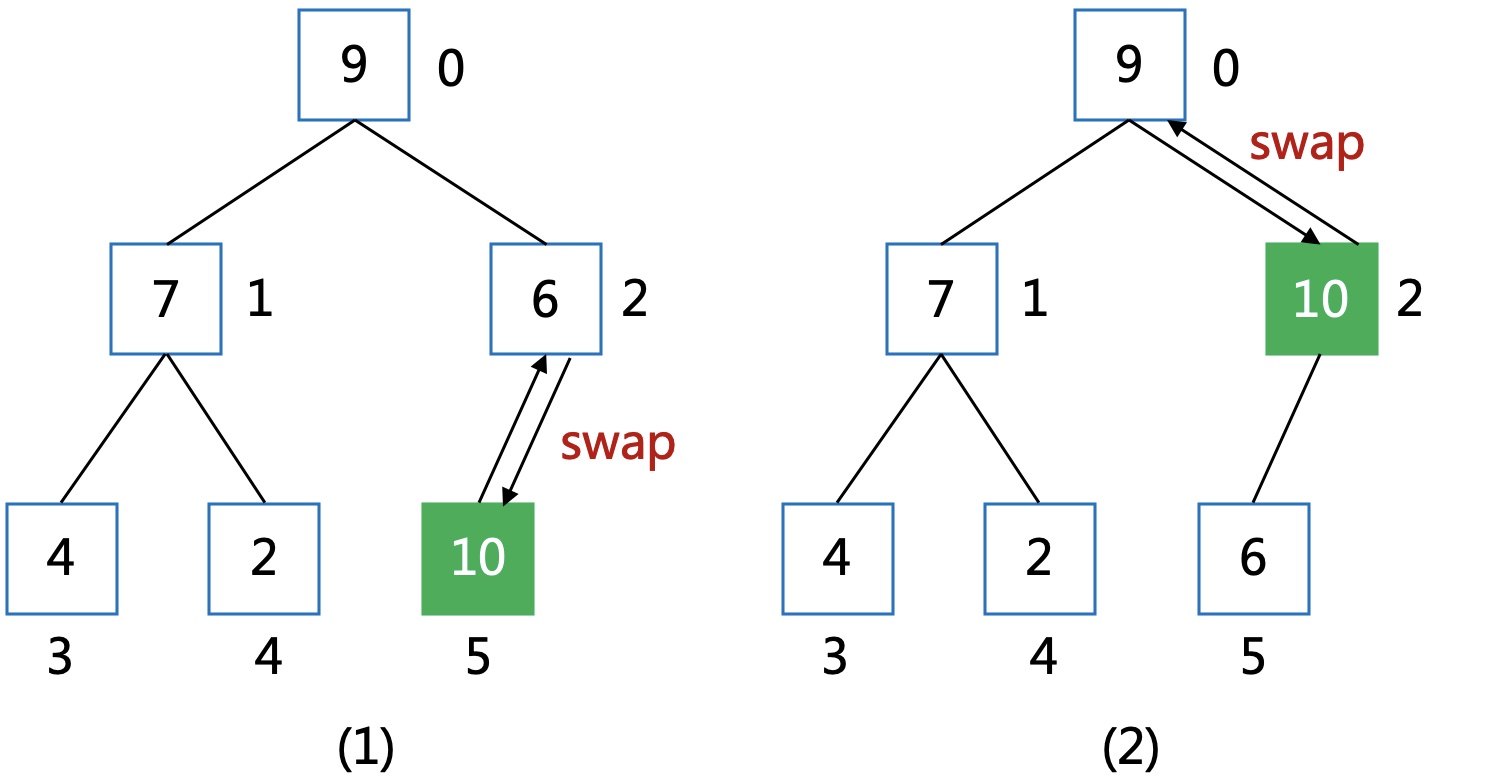
代码实现
//将heap[k]向上调整
int heapUp(int *heap, int k) {
int parent, son, x;
x = heap[k];
son = k;
parent = (son - 1) / 2;
while (son > 0) {
//如果父结点大于等于heap[k]则退出,否则将父结点下移
if (heap[parent] >= x)
break;
heap[son] = heap[parent];
son = parent;
parent = (son - 1) / 2;
}
heap[son] = x;
return 0;
}
父结点与子结点的下标关系如下:
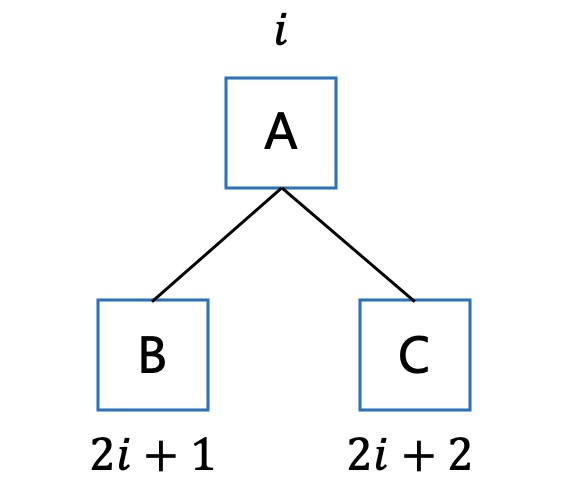
用一个指针指向待调整的结点:
直到指向叶子结点或者当前结点大于两个子结点。
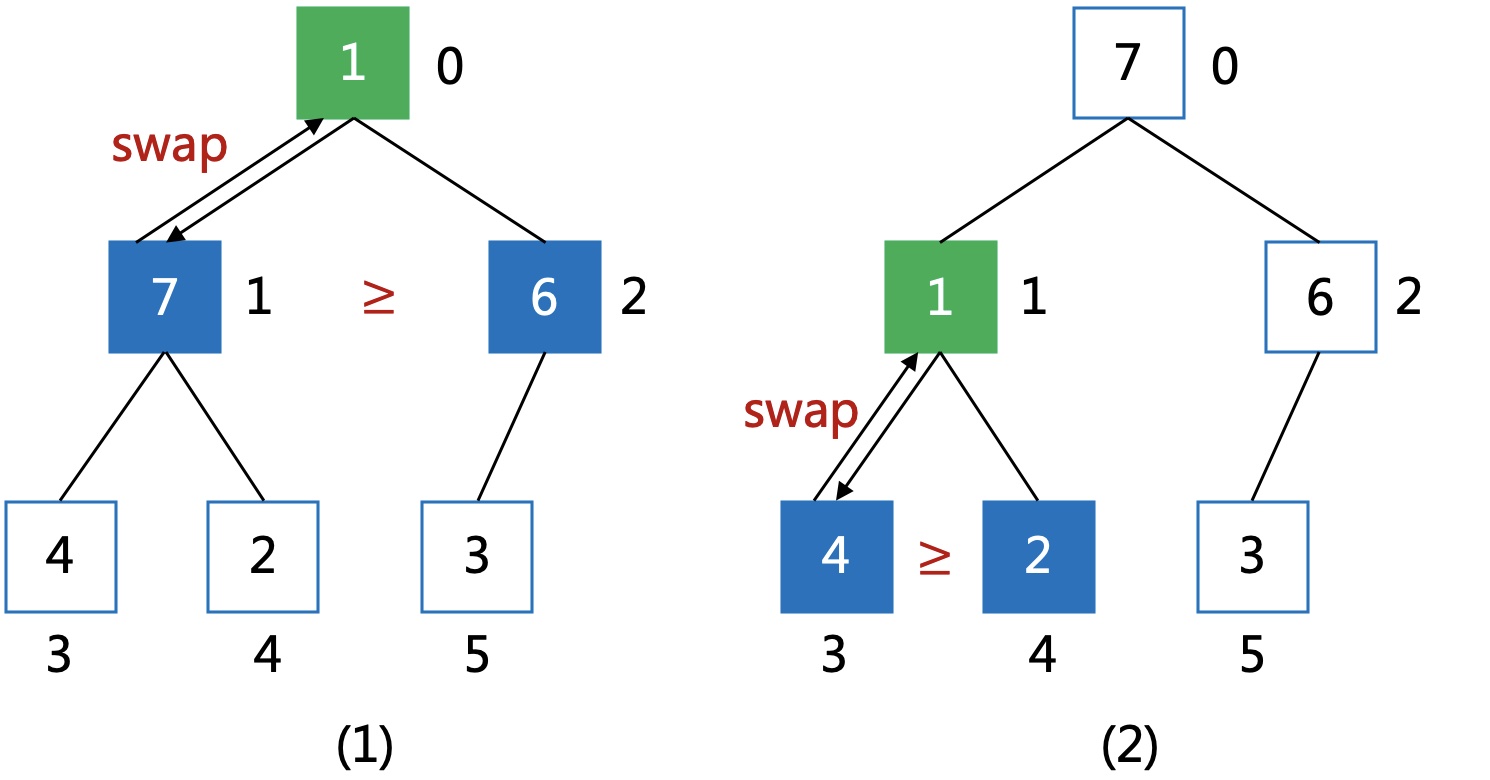
代码实现
//将heap[k]向下调整
int heapDown(int *heap, int k, int n) {
int parent, son, x;
x = heap[k];
parent = k;
son = 2 * k + 1; //左孩子结点
while (son <= n) {
//比较左右儿子,选择较大的一个
if (son + 1 <= n && heap[son + 1] > heap[son])
son++; //使son指向左右孩子中较大的结点。
//如果儿子结点中较大的都小于等于待调整结点则退出,否则将子结点上移
if (heap[son] <= x)
break;
heap[parent] = heap[son];
parent = son;
son = 2 * parent + 1;
}
heap[parent] = x;
return 0;
}
从堆尾插入元素,再对该元素进行向上调整直到满足堆性质。
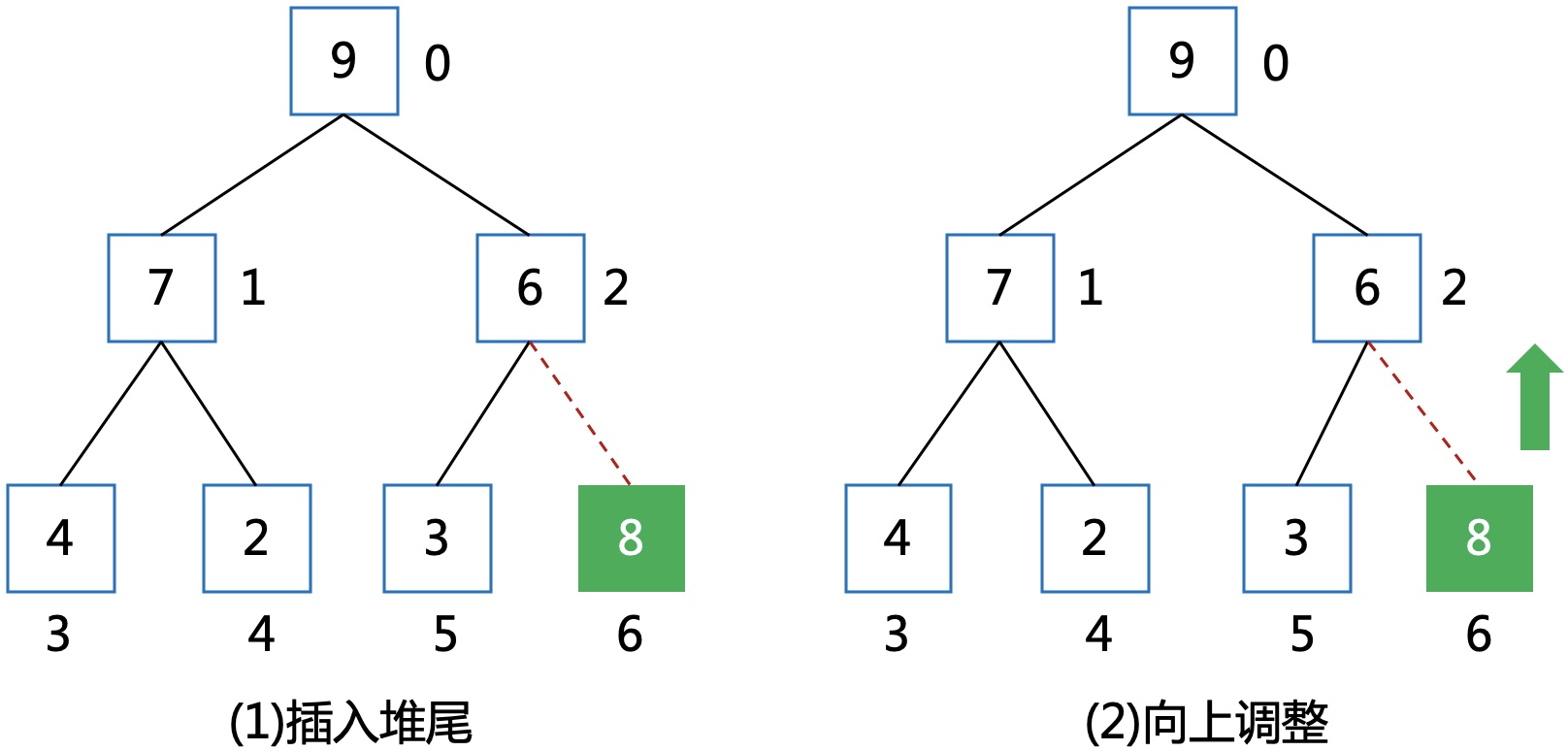
将堆顶弹出,用堆尾的元素置换,再对堆顶的元素进行向下调整。
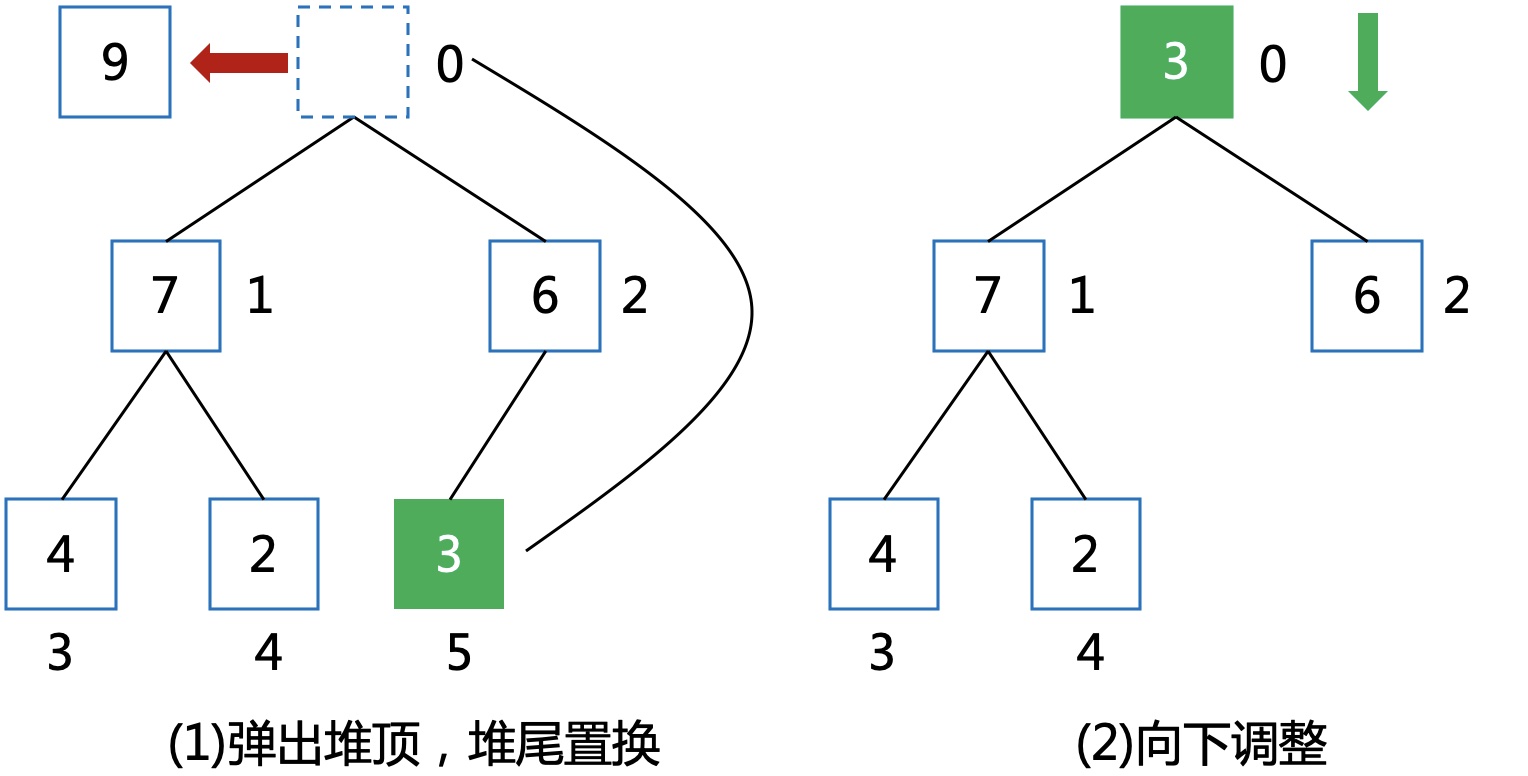
依次向堆尾插入元素,并对该元素进行向上调整,直到满足堆性质。
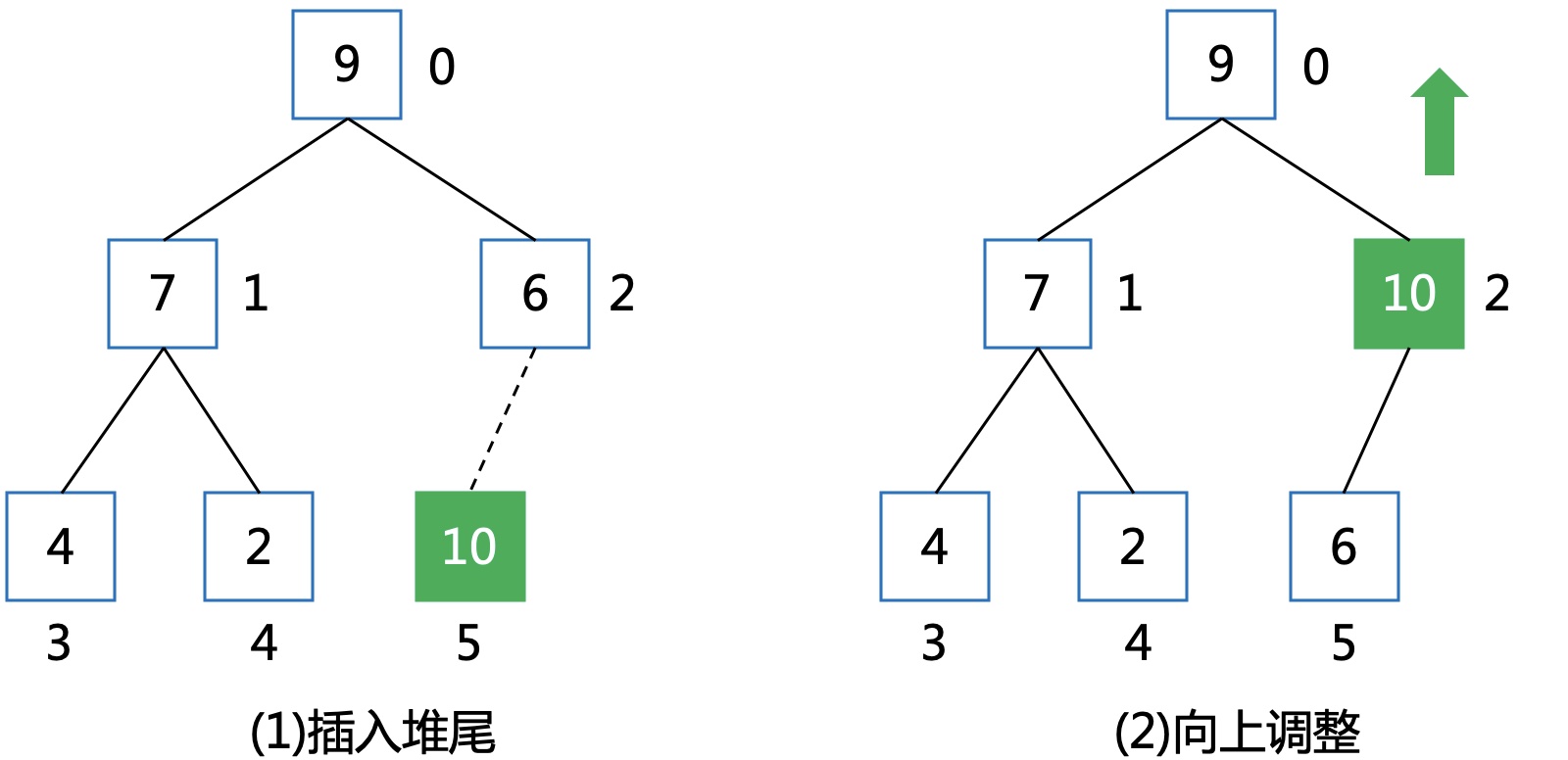
时间复杂度:
插入一个元素要调整的高度为logi,所以插入n个元素的总次数为log1+log2+...+logn=log(n!)。
根据斯特林公式,有如下证明,所以复杂度O(nlogn)。
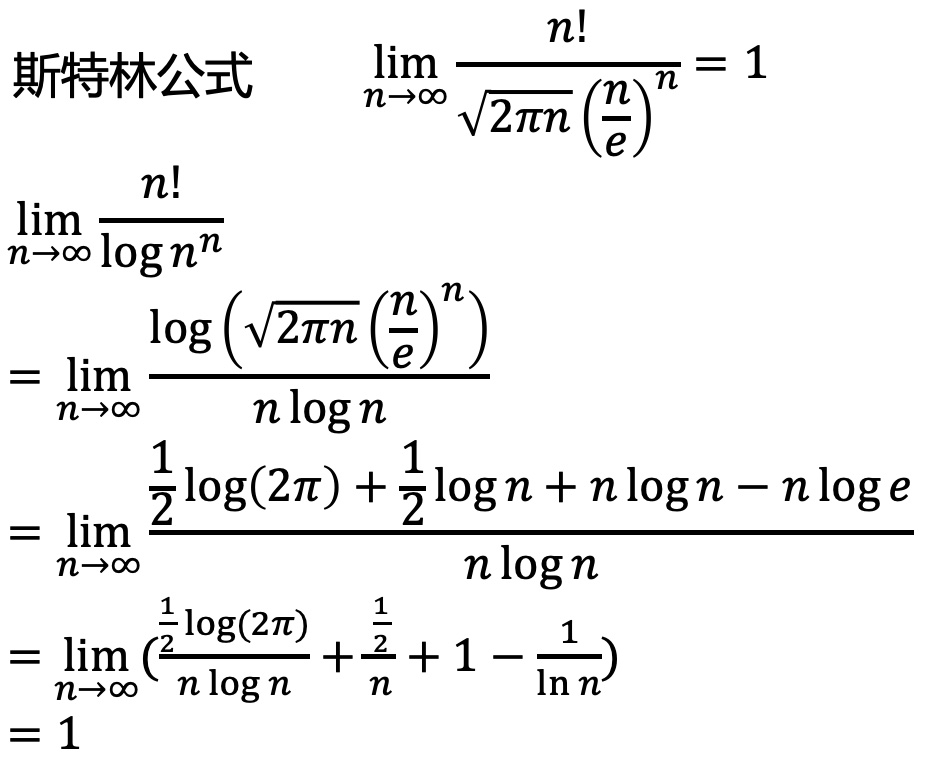
待调整的数组,可以直接看成是一棵完全二叉树。
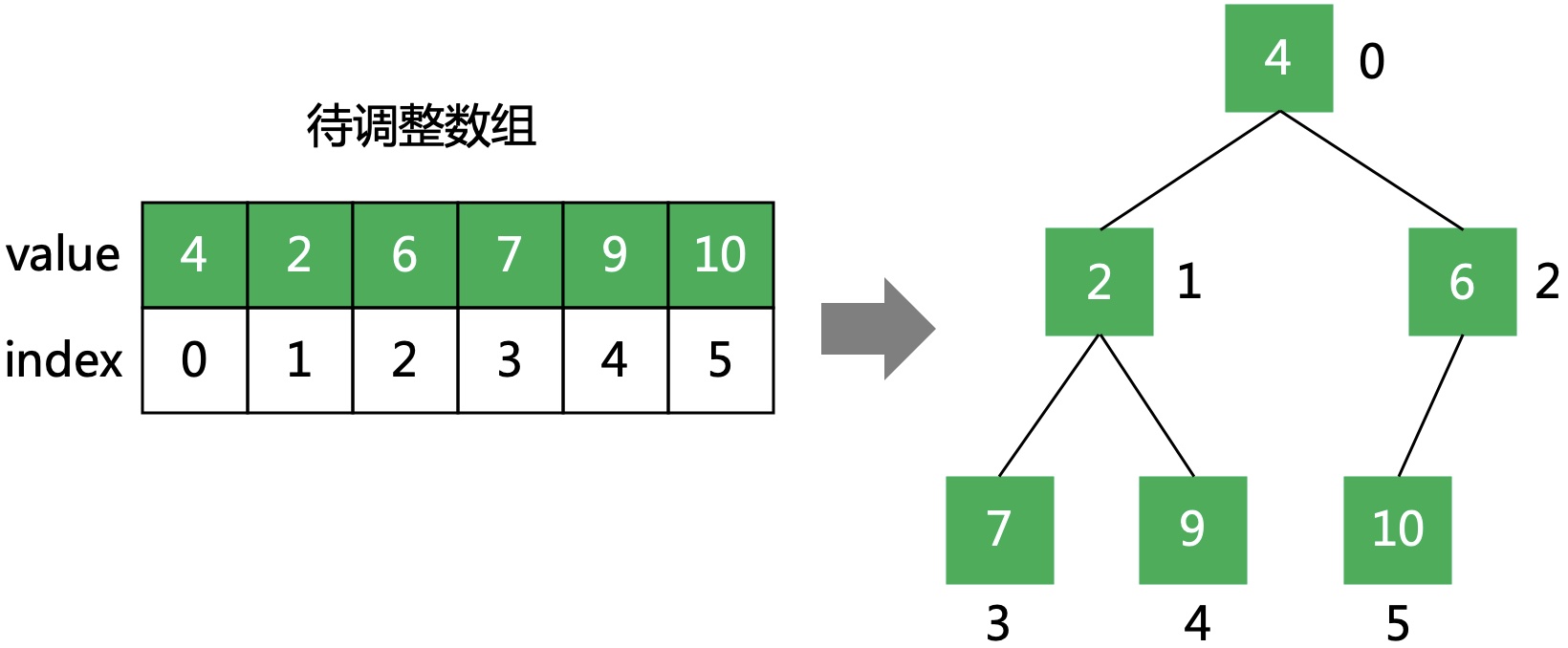
从(n-1)/2位置开始,将每个元素进行向下调整,直到根结点。对于每一个待调整的当前结点,下面的子树都已经满足堆性质,所以调整完所有结点便成了堆。
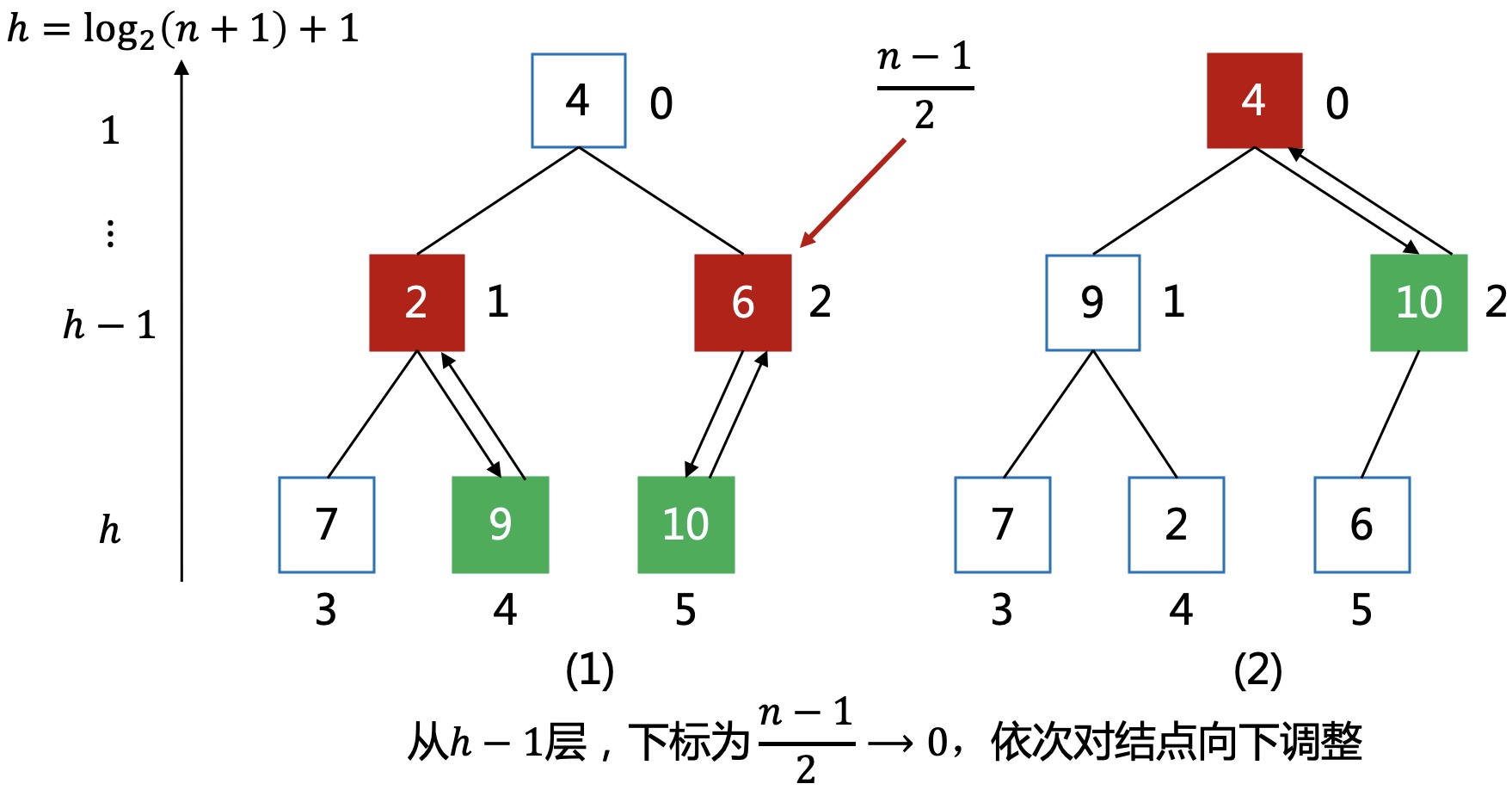
时间复杂度:
倒数第二层有2^(h-2)个结点,调整高度为1,依次类推,第一层有1个结点,调整高度为h-1,整体加起来的复杂度为O(n)。
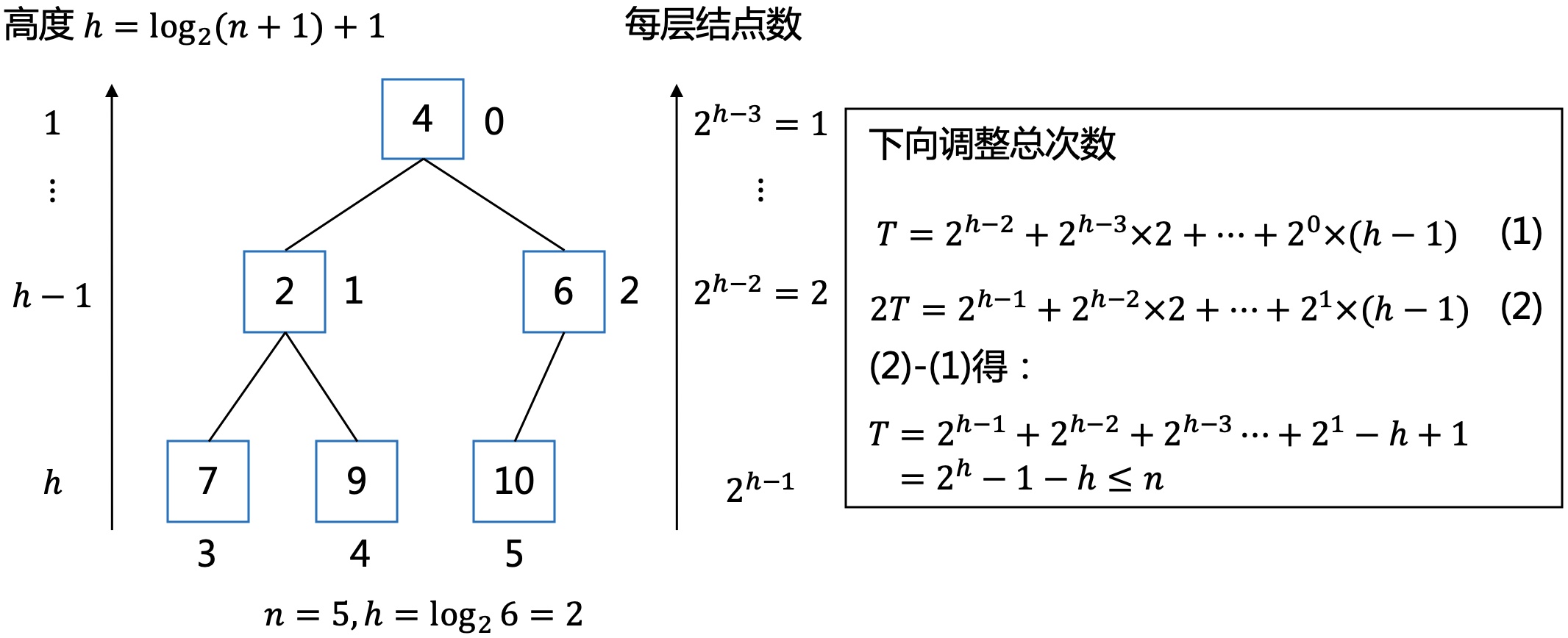
代码实现
void buildHeap(int *heap, int n) {
for (int i = (n - 1) / 2; i >= 0; --i) {
heapDown(heap, i, n);
}
}
一个已经调整完成的大根堆。
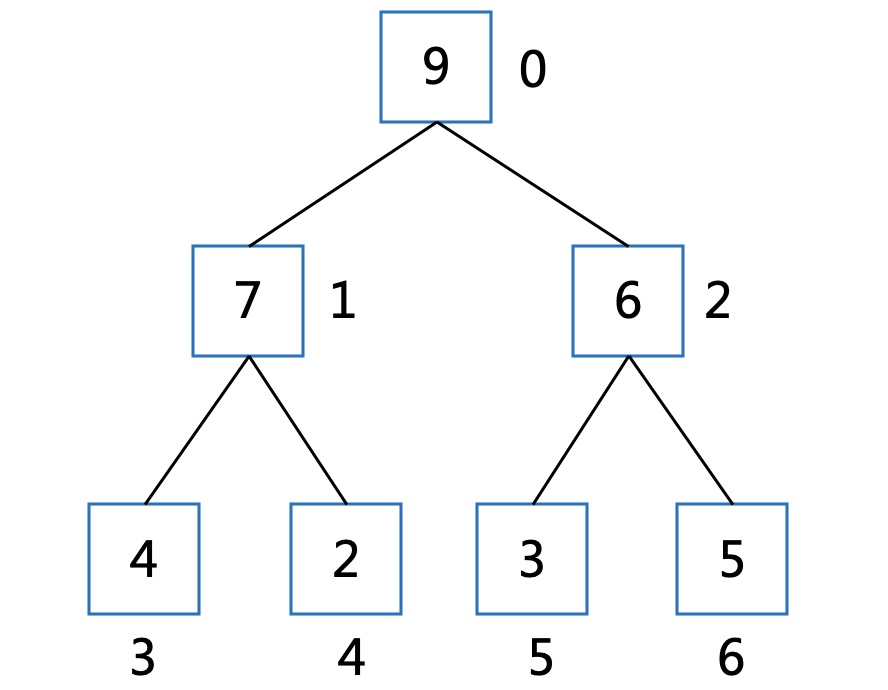
核心思想:
重复以上过程直到整体元素为1,这时就变成了一个升序排列的数组。
模拟过程:
Step 1
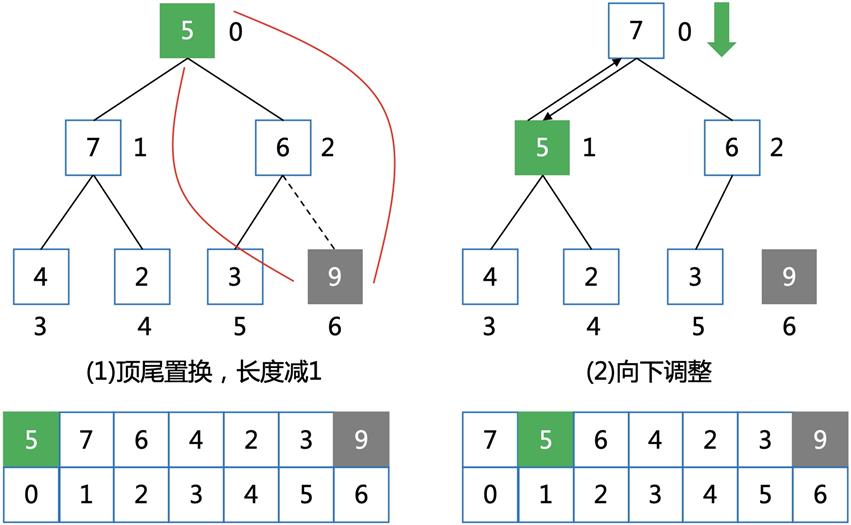
Step 2
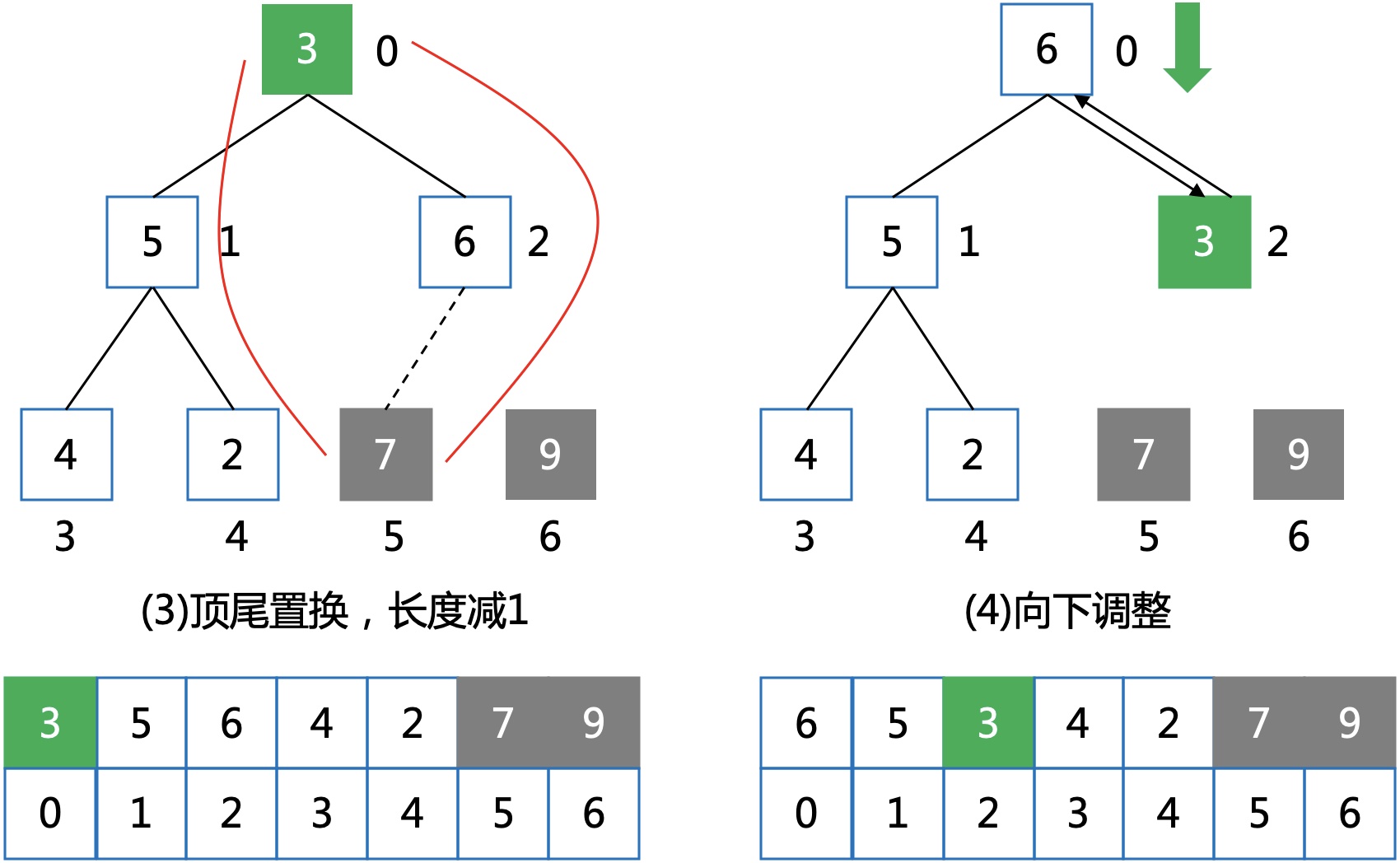
堆排的复杂度为nlogn,应用场景很广泛,这篇文章主要讲清楚堆相关的操作,具体的应用和建模以后会再专门写文章讲解。
如果喜欢小K的文章,请点个关注,分享给更多的人,小K将持续更新,谢谢啦!
扫描下方二维码关注公众号:小K算法,第一时间获取更新信息!

原文:https://www.cnblogs.com/kylewilson/p/14713543.html