首先我们有这样一个例子,假设我们要通过一个品牌的各种广告方式来提高这个品牌产品的销售量。我们拿到这么一个数据,\(S = \{sales, TV, ratio, newpaper\}\)。公司当然不能直接提高产品的销售额,能控制得是在三个媒体渠道投入的资产。如果我们发现了广告和销售额之间的关系,那么,我们就能指导企业来调整广告投入分配。换句话说,我们要建立一个准确的模型,而这个模型可以通过三个渠道的广告方式的预算数据来预测销售额。
在这个情况下,{TV, ratio, newspaper}就是我们的输入变量(预测变量、特征、解释变量等等),而{sales}就是我们的输出变量。输入变量我们一般用\(X = \{X_1, X_2,...,X_d\}, X \in R^{n\times d}\) 来表示我们有n组数据,每组数据有d个维度。 sales就是我们的输出变量(响应变量),通常用\(Y = \{Y_1,...,Y_m\}, Y \in R^{n\times m}\)来表示。假设Y和X之间具有一些关系,则我们可以写成如下形式。
从另一个角度来说,\(f\)是\(X\)所能提供的对于\(Y\)的系统性的信息。
我们有很多线性或者非线性的模型来估计这个映射函数\(f\),但是每个方法都有一些共通的性质,这个部分会介绍这些共同的特点。 在介绍前先确定一些术语:
明确我们的目标:通过在训练数据上建立模型来找到那个未知的函数\(f\)。
总的来说,统计学习方法可以分为参数方法和非参数方法,这里我们简单地介绍两种类型
参数方法可以分为两个步骤。
这就是线性模型,之后会详细地介绍。一旦确立了模型地样子,问题就变得相对简单了,我们只需要去想办法估计这些参数。比如在线性模型里,我们就要估计p+1个参数\(\beta_0,\beta_1,...,\beta_p\)
参数方法存在一个潜在的问题:我们选择的f的模型形式往往和真实的模型形式不是相同的。我们很难做到准确地设定我们都模型。如果我们设定地模型和原模型差距过大,那效果也会很差。为了解决这个问题,我们可以尝试不同地灵活地模型,但是这样就意味着我们需要估计更多地参数并且复杂地模型还有可能导致过拟合(overfitting)的问题
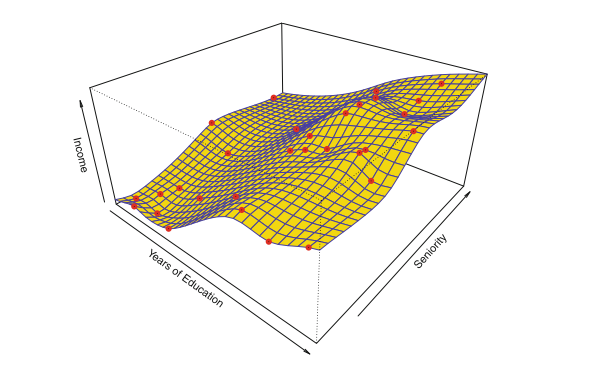
非参数方法不需要对模型的形式做出假设,它找的是f的一个估计去使得它尽量接近数据点但又不是太粗糙或模糊。这么通过避免假设f具有特定的函数形式,它们有可能准确地拟合f的更广泛的可能形状。但是非参数方法确实有一个主要的缺点:由于它们不能将估计f的问题减少到少量参数,因此需要大量的观测值(远远超过参数方法通常所需的观测值)。 为了获得f的准确估计。
绝大多数统计学习问题都可以分为监督学习和无监督学习(实际上也有半监督学习)。一些经典的学习模型像线性回归、逻辑回归、GAM、boosting、支撑向量机等都是在有监督学习的领域内的。相反,无监督学习描述了一种更具挑战性的情况,那就是我们只有观测值\(x_i\)而没有其对应的标签或响应值\(y_i\)。这种情况下,我们当然没法去用线性模型因为没有响应变量。
对于这种情况,我们追寻的是去理解和找寻观测值或变量之间的关系。常用的方法是聚类方法,其目的是在观测值的基础上去确定观测值是否落在相对不同的群(group)中。
许多问题自然属于有监督或无监督的学习范式。但是,有时分析应被视为监督还是无监督的问题却不太明确。例如,假设我们有一组n个观测值。对于m个观察值中的\(m<n\),我们既有预测值也有响应值。对于其余的n-m个观测值,我们有预测值测量值,但没有响应测量值。如果可以相对便宜地测量预测变量,但收集相应的响应要昂贵得多,则会出现这种情况。我们将此设置称为半监督学习问题。
变量可以分为定量或者定性(分类)变量。定量变量展现出来时数值形式,比如人的身高、体重、收入等。相反,定性变量展现出来的是不同的类别或级别,例如人的性别、公司品牌等。如果我们的响应变量是一个定量的变量,我们常将此类问题成为回归问题。如果响应变量是一个定性的变量,我们常常称这种问题为分类问题。
最小二乘线性回归使用的就是定量的响应变量,而逻辑回归中使用的响应变量是一个定性变量(分类变量)
原文:https://www.cnblogs.com/DS-blog-HWH/p/14716384.html