树与查找

目录

1. 查找的基本概念

2. 二叉树排序

3. 疑难问题

查找的基本概念

查找表

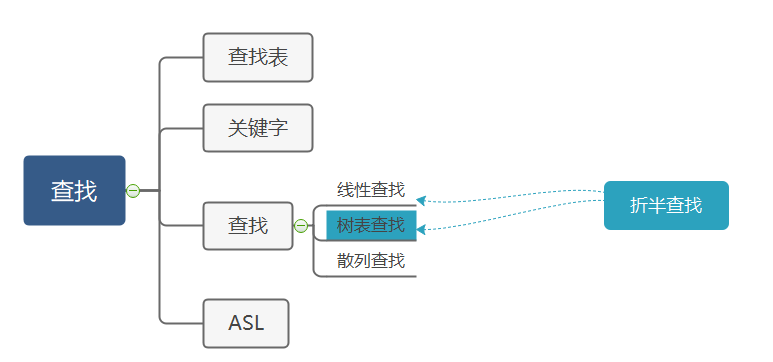
运作查找算法的载体，可以使用多种数据结构来实现。

关键字

关键字是数据元素或记录中某个数据项的值，用它可以标识一个数据元素或记录。

查找

通过关键字，向查找表索要数据的行为。

ASL

平均查找长度，在查找操作中和给定值进行比较的关键字个数的期望值。公式

线性查找

树表查找

线性查找对修改数据时内存开销较大，只适合静态查找。为此，用树表来进行动态查找的树结构便担此重任。

散列查找

二叉树排序

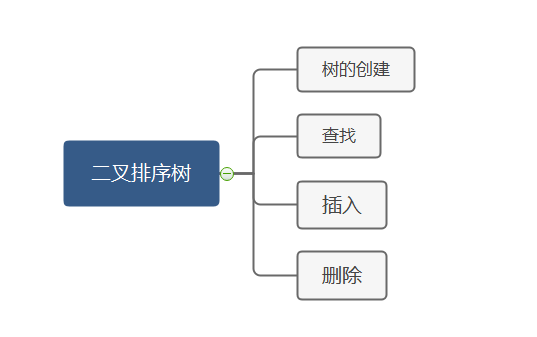
二叉排序树又称二叉搜索树，其定义为二叉排序树或是空树，或者是满足以下性质的二叉树:

1. 若根节点的左子树非空，则右子树上的所有结点关建字均小于根节点。
2. 若根节点的右子树非空，则右子树上的所有结点关键字均大于根节点。
3. 根节点的左、右子树本身右各是一棵二叉排序树。

?

树的创建

typedef struct BST      //结点类型
{
	Type key;
	struct BST *lchild,*rchild; 
}BSTNode;

void CreatBST(BST*&T)    //创建结点
{
	T=new BST;
	T=NULL;
}

查找

BST *SearchBST(BST *T,Type key)
{
	if(T==NULL||T->key==key)
		return T;
	if(key<T->key)
		return SearchBST(T->lchild,key);
	else
		return SearchBST(T->rchild,key);
}

插入

bool InsertBST(BST*&T,Type key)
{
	if(T==NULL)
	{
		T=new BST;
		T->key=key;
		T->lchild=T->rchild=NULL;
		return true;
	}
	else if(key==T->key)
		return false;
	else if(key<T->key)
		return InsertBST(T->lchild,key);
	else if(key>T->key)
		return InsertBST(T->rchild,key);
}

删除

删除分为四种情况

1. 该结点只有左树，则用左孩子取代，即返回左孩子地址；
2. 该孩子只有右树，同第二种情况。返回右孩子；
3. 该结点为叶子结点，则在递归中直接返回NULL；
4. 该孩子既有左树又有右树。我的思路是找一个最靠近该结点的值，取代结点并删掉他。通过二叉树的构造特点，左树的最小值和右树的最大值都是最靠近该结点的，这里我选用后者。

BST* Deletemin(BST*bt,BST *&min)      //找到右树最小值，在引用中直接赋值
{
	if(bt->lchild==NULL)
	{
		min=bt;       //没有左孩子，根节点最小 
		return bt->rchild; 
	}
	bt->lchild=Deletemin(bt->lchild,min);    //用递归的方法更新树
	return bt;
}

BST*DeleteBST(BST *bt,Type key)
{
	if(bt==NULL)return NULL;
	if(bt->key>key)
	bt->lchild=DeleteBST(bt->lchild,key);
	else if(bt->key<key)
	bt->rchild=DeleteBST(bt->rchild,key);
	else
	{
		if(bt->lchild==NULL)
		bt=bt->rchild;
		else if(bt->rchild==NULL)
		bt=bt->lchild;
		else
		{
			BST*min;
			min=NULL;
			bt->rchild=Deletemin(bt->rchild,min);
			bt->key=min->key;
		}
	}
	return bt;
}

其中，在删除结点的适合以上我用的是递归的方法更新树，当然我发现其他同学也有用循环的方法，各有特点。

疑难问题

作者在编写删除操作时，习惯性地用delete直接删除结点

void deleteBST(BST *T,Type key)
{
	BST *p，*q;
	p=Search(T,key);
	if(!p)
	{
	cout<<"找不到"；
	return； 
	} 
	else 
	{
        delete p；
        }
}

看似理所当然，但是这回导致非叶子结点的结点删除自己的子树，所以这里作者用递归，不断更新删除后的结点，如 删除

参考资料

《数据结构教程（第5版）》——李春葆 主编，清华大学出版社

数据结构——树与查找

原文：https://www.cnblogs.com/ulage/p/14720297.html