树与二叉树思维导图

重要概念

树与二叉树的基本概念

树与二叉树的定义

• 树(Tree)是由一个或多个结点组成的有限集合T，其中有一个特定的称为根的结点；其余结点可分为m(m≥0)个互不相交的有限集T1,T2,T3 ,…,Tm，每一个集合本身又是一棵树，且称为根的子树。
• 二叉树是一种重要的树形结构，其结构定义为：二叉树是n(n≥0)个结点的有限集，它或为空树(n=0)，或由一个根结点和两棵分别称为根的左子树和右子树的、互不相交的二叉树组成。
• 满二叉树是一棵深度为k，且有2k - 1个节点的树。
• 完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

二叉树的存储结构

• 顺序存储结构
  
• 链式存储结构
  

二叉树的遍历

• 二叉树的类型声明

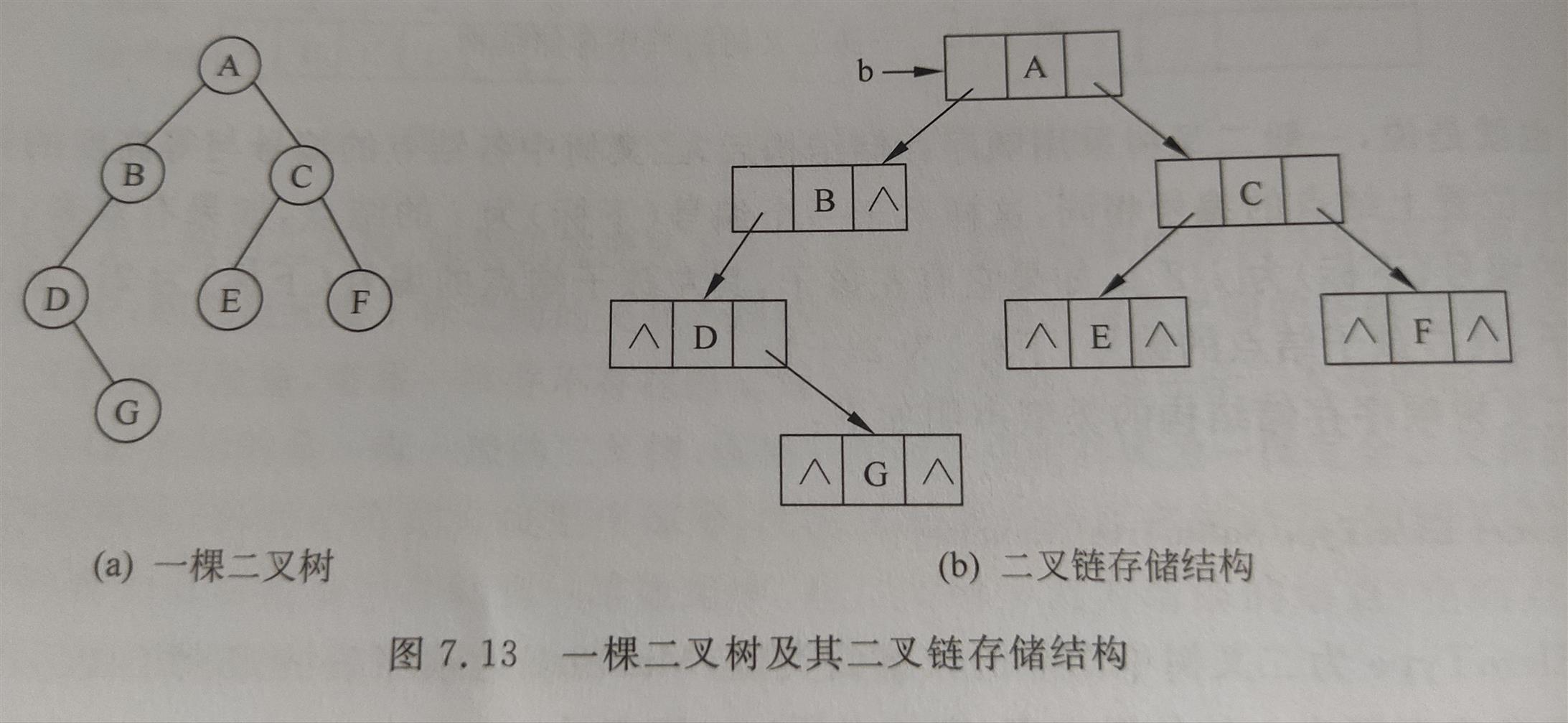
typedef int ElemType;
typedef struct node {
	ElemType data;
	struct node* lchild;
	struct node* rchild;
}BTNode;

• 先序遍历

void PreOrder(BTNode* b) {//先序遍历递归算法
	if (b != NULL) {
		cout << b->data << endl;//访问根节点
		PreOrder(b->lchild);//先序遍历左子树
		PreOrser(b->rchild);//先序遍历右子树
	}
}

• 中序遍历

void InOrder(BTNode* b) {//中序遍历递归算法
	if (b != NULL) {
		InOrder(b->lchild);//中序遍历左子树
		cout << b->data << endl;//访问根结点
		InOrder(b->rchild);//中序遍历右子树
	}
}

• 后序遍历

void PostOrder(BTNode* b) {//后序遍历递归算法
	if (b != NULL) {
		PostOrder(b->lchild);//后序遍历左子树
		PostOrder(b->rchild);//后序遍历右子树
		cout << b->data << endl;//访问根结点
	}
}

线索二叉树

• 线索二叉树的类型声明

typedef int ElemType;
typedef struct node {
	ElemType data;//结点数据域
	int ltag, rtag;//增加的线索标记
	struct node* lchild;//左孩子或线索指针
	struct node* rchild;//右孩子或线索指针
}TBTNode;//线索二叉树中的结点类型

• 中序线索二叉树

TBTNode* pre;//全局变量
void Thread(TBTNode*& p) {//对二叉树p进行中序线索化
	if (p != NULL) {
		Thread(p->lchild);//左子树线索化
		if (p->lchild == NULL) {//左孩子不存在，进行前驱结点线索化
			p->lchild = pre;//建立当前结点的前驱结点线索
			p->rtag = 1;
		}
		else//p结点的左子树已线索化
			p->ltag = 0;
		if (pre->rchild = NULL) {//对pre的后继结点线索化
			pre->rchild = p;//建立前驱结点的后继结点线索
			pre->rtag = 1;
		}
		else
			pre->rtag = 0;
		pre = p;
		Thread(p->rchild);//右子树线索化
	}
}
TBTNode* CreateThread(TBTNode* b) {//中序线索化二叉树
	TBTNode* root;
	root = (TBTNode*)malloc(sizeoí(TBTNode));//创建头结点
	root->ltag = 0; root->rtag = 1;
	root->rchild = b;
	if (b == NULL)//空二叉树
		root->lchild = root;
	else {
		root->lchild = b;
		pre = root;//pre是结点p的前驱结点，供加线索用
		Thread(b);//中序遍历线索化二叉树
		pre->rchild = root;//最后处理，加入指向头结点的线索
		pre->rtag = 1;
		root->rchild = pre;//头结点右线索化
	}
	return root;
}

• 遍历线索化二叉树

void ThInOrder(TBTNode* tb) {//tb指向中序线索二叉树的头结点
	TBTNode* p = tb->lchild;//p指向根节点
	while (p != tb) {
		while (p->ltag == 0)
			p = p->lchild;//找开始结点
		cout << p->data;//访问开始结点
		while (p->rtag == 1 && p->child != tb) {
			p = p->rchild;
			cout << p->data;
		}
		p = p->rchild;
	}
}

树与二叉树

原文：https://www.cnblogs.com/xypeanut/p/14722912.html