树的基本概念

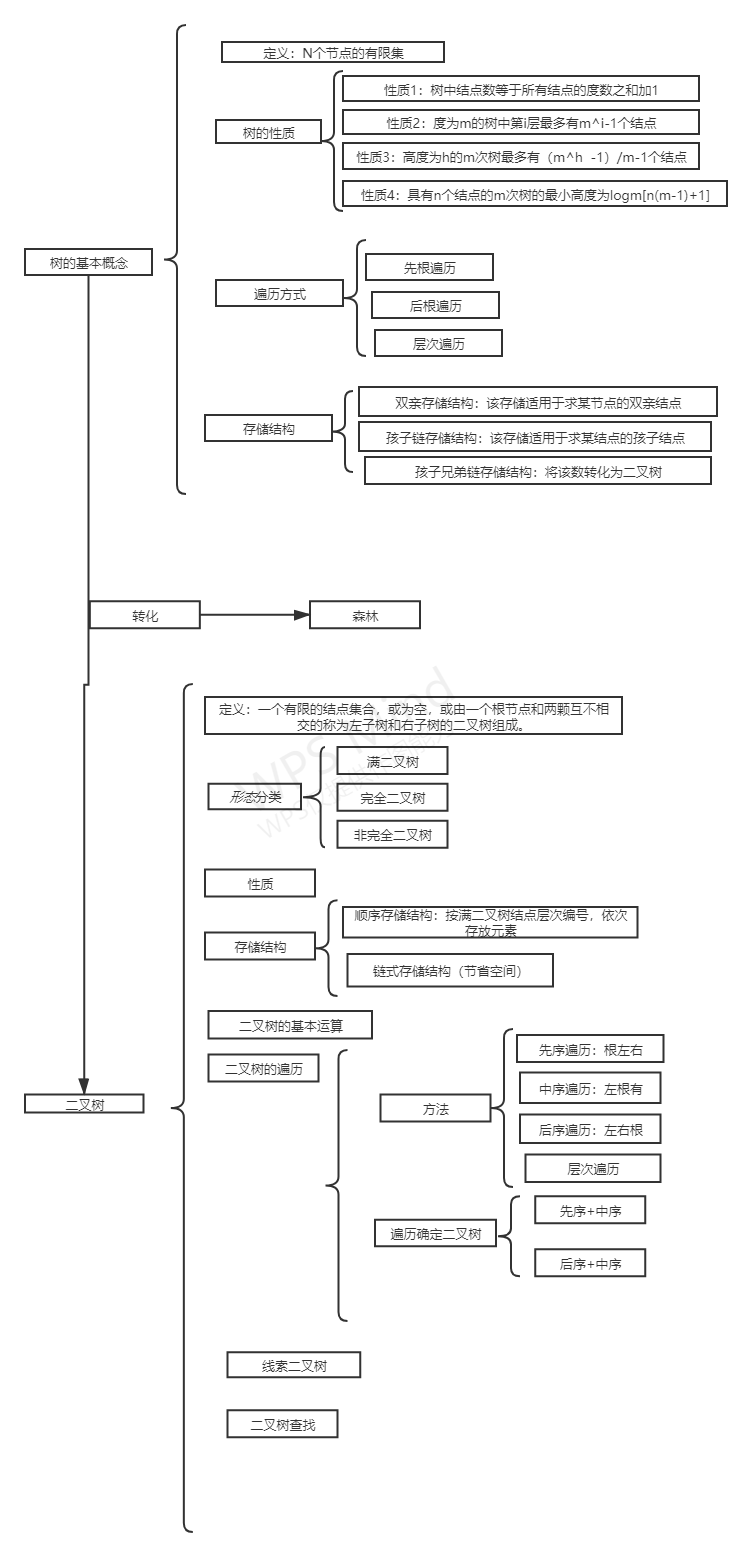
（1）树结构常用于表示具有层次结构的数据，体现一对多的关系。
（2）树的定义是递归的。
（3）有序树是树中各节点的子树按照一定次序从左向右安排的，且相对次序是不可以随意改变的；否则为无序树。

二叉树的基本概念

有关完全二叉树的计算

（1）由结点总数n 求叶子结点n。：

n。=（n+1）/2  [n为奇数]
n。= n/2  [n为偶数]

（2）由结点总数n 求度为1的结点个数

n为奇数，n1=0;
n为偶数，n1=1;

使用栈将递归中序遍历改为非递归

递归算法

//先序遍历
void preorder(BTNode *b)
{
if(b!=NULL)
{
printf("%c",b->data);
preorder(b->lchild);
preorder(b->rchild);
}
}
//中序遍历
void inorder(BTNode *b)
{
if(b!=NULL)
{
inorder(b->lchild);
printf("%c",b->data);
inorder(b->rchild);
}
}
//后序遍历
void postorder(BTNode *b)
{
if(b!=NULL)
{
postorder(b->lchild);
postorder(b->rchild);
printf("%c",b->data);
}

中序遍历非递归算法

void inorder(BTNode *b)
{
BTNode *p;
SqStack *st;
InitStack(st);
p=b;
while(!StackEmpty(st)||p!=NULL)
{
while(p!=NULL)
{
push(st,p);
p=p->lchild;
}
if(!StackEmpty(st))
{
pop(st,p);
printf("%c",p->data);
p=p->rchild;
}
}
printf("\n");
DestroyStack(st);
}

线索二叉树

优点：加快查找节点的前驱和后继的速度，并且充分利用了空指针域的空间。

二叉树线索化：增设头结点，线索化的二叉树就如同双向链表，即可正向遍历，也可逆向遍历。

遍历线索二叉树：可以通过之前建立好的线索，沿着后继线索开始访问下去。

疑难问题

如何判断二叉树是否是平衡二叉树（AVL树）

（1）性质：它是一棵空树或以当前结点为根结点的树，左右子树的深度不得超过1。
（2）解决方法：判断该树是否为空，如果为空则是平衡二叉树，如果不为空，判断左右子树高度差绝对值是否大于1，如果大于则不是平衡二叉树，否则递归遍历每个节点左右子树，诺所有结点左右子树高度差的绝对值均不大于1，则为平衡二叉树。

树、二叉树的基本概念

原文：https://www.cnblogs.com/wsj2496/p/14722001.html