动量定理中绳问题的微元解法

问题引入

已知一段软绳，其长度为$L$，其线密度为$\lambda$，一段恰好接触地面且垂直于地面放置，求证：下落时地面对绳的支持力等于已落地部分绳的重力的$3$倍

证明

设下落时间为$t$，则在空中绳长为$L-\frac{1}{2}gt^{2}$，在空中绳质量为$m=\lambda(L-\frac{1}{2}gt^{2})$，落地速度为$v=gt$

可列出方程组

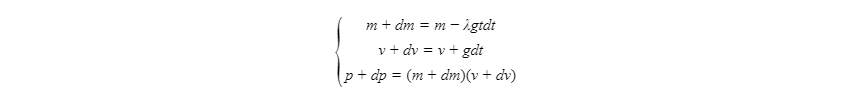
 所以$p+dp=p+mgdt-\lambda g^{2}t^{2}dt-\lambda g^{2}td^{2}t^{2}$其中二阶无穷小等于$0$，所以我们可以得到

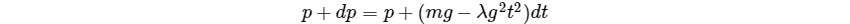
 即

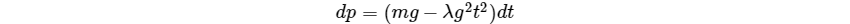
 而根据动量定理，我们又可得到

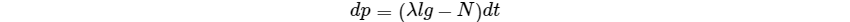
 联立并约去$dt$得到

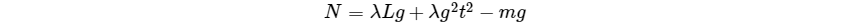
 将$m=\lambda(L-\frac{1}{2}gt^{2})$带入，解得

动量定理中绳问题的微元解法

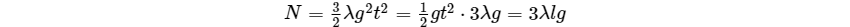
原文：https://www.cnblogs.com/Tenderfoot/p/14723030.html