一、Floyd算法的本质

dijkstra是基于贪心的做法，而bellman-ford和floyd都是基于DP的做法。floyd是如何进行DP的？

f[k,i,j] 表示所有从i出发，走到j的，中间只经过结点编号小于等于k的所有路径。

二、Floyd算法的用处

1.求最短路

2.求传递闭包

3.求最小环

4.求恰好经过k条边的最短路

 三、求最短路和传递闭包

1.牛的旅行

https://www.acwing.com/problem/content/1127/

枚举结合Floyd求最优化问题

2.产生数、排序

https://blog.csdn.net/numb_ac/article/details/104122491

https://www.acwing.com/problem/content/345/

求传递闭包，注意确定关系的条件和出现矛盾的条件怎么进行判断。对于本题，矛盾情况为d[i][i]=1（相当于同时出现了i>j 且 j>i）,唯一确定情况为对于每组的i和j，d[i][j]和d[j][i]必有一个为1。

输出顺序，因为这道题是从小到大输出，那么就每次找最小的然后剔除掉就好了。写一个get_min函数，每次找没被输出的且最小的，判断最小的方法就是没有其它的比它小。

四、求最小环

1.观光之旅

https://www.acwing.com/problem/content/346/

1)从集合的角度来分析最优化问题，按环上编号最大的点对集合进行划分。而这恰好和Floyd算法的性质吻合。

2)考虑对于外层循环k来看，当进行到第k次外层循环的时候，说明已经求出了d[i][j]的，只用1~k-1的点转移的最短路。如图1所示。又显然1~k-1这些点都是小于k的，

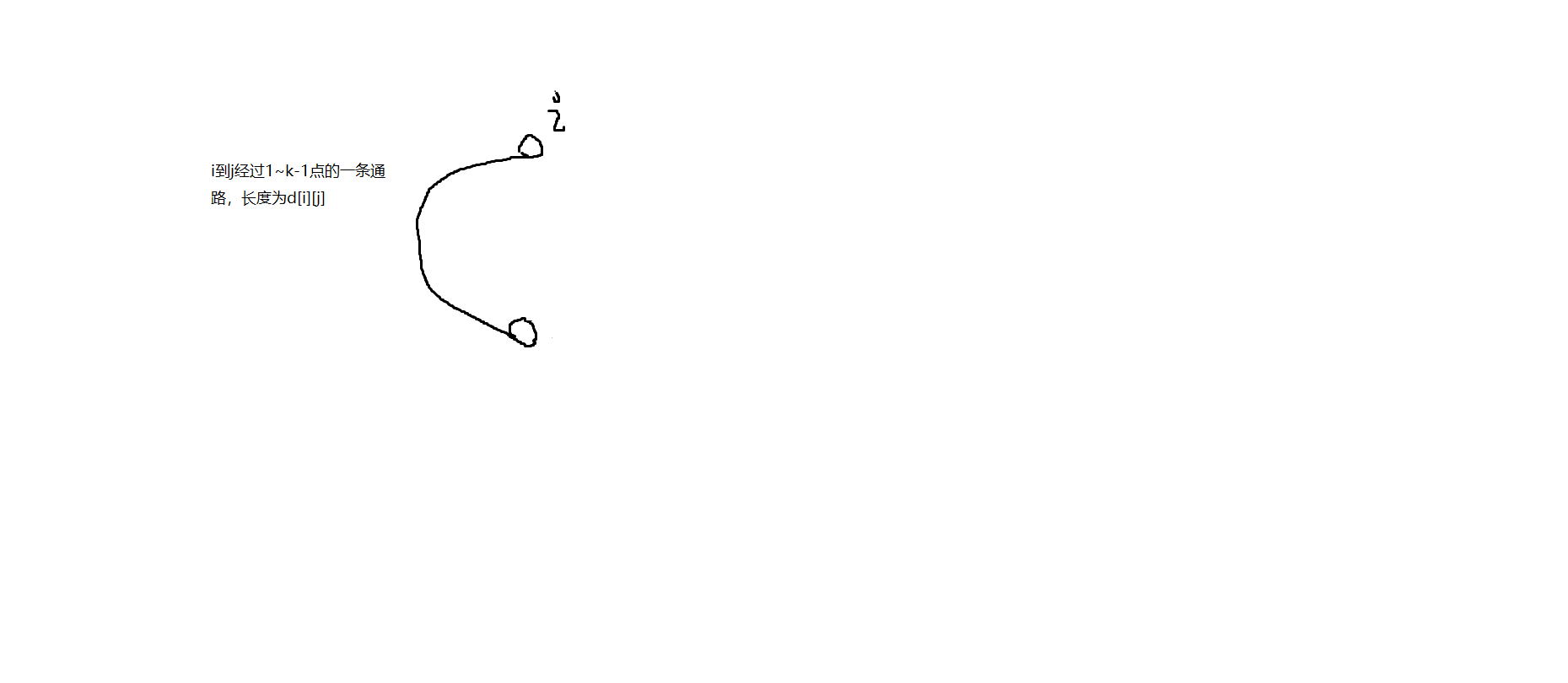
图1

然后再把k加进来，就能得到一个环上最大编号为k的环了。如图2所示。

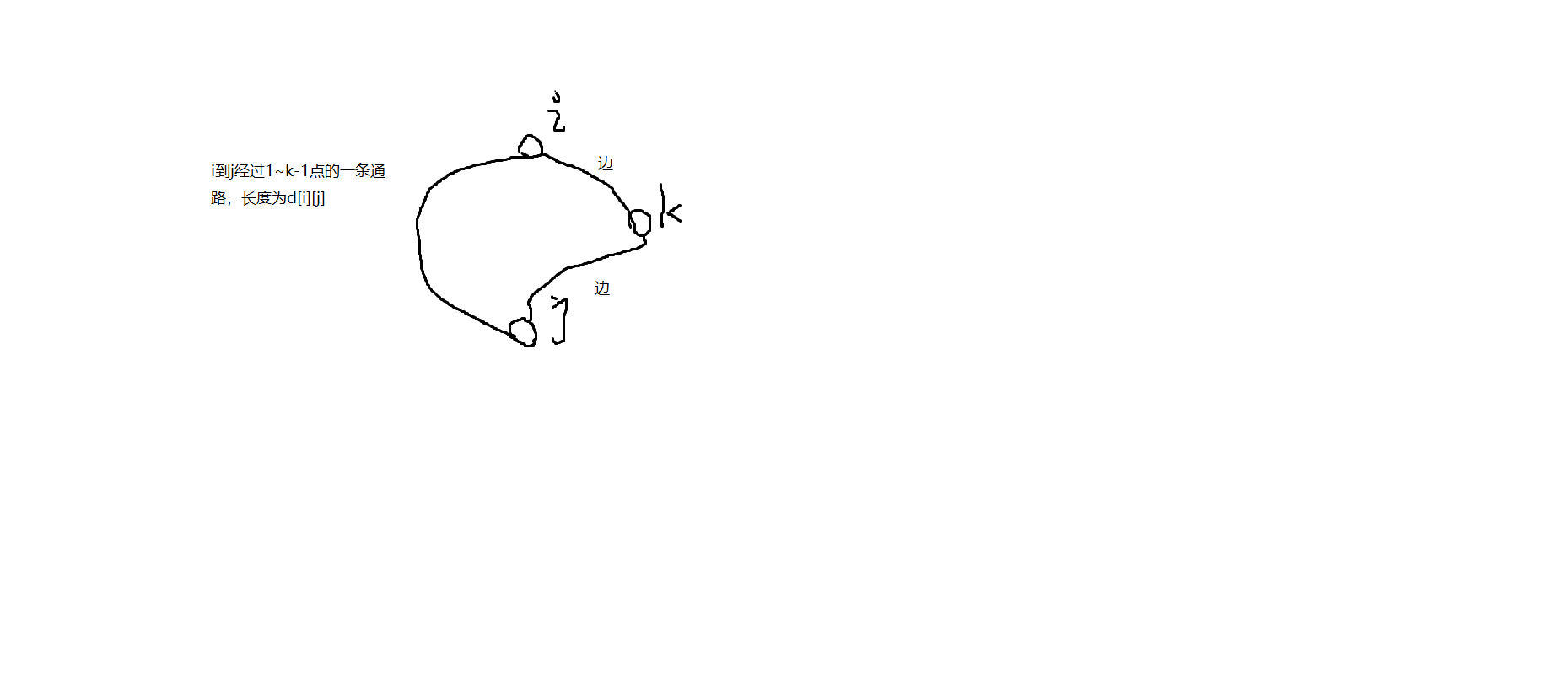
图2

五、恰好经过k条边的最短路（其实这不是Floyd算法，是一个特殊的DP）

d[k][i][j]现在变为从i到j恰好经过k条边的路径

d[a+b,i,j]=min{d[a,i,k]+d[b,k,j]} ，k从1到n取，就能取到所有从i到j恰好经过a+b条边的情况
上面的k指的是i经过a条边之后的点是k

(倍增优化待续）

图论知识点总结2 Floyd算法（实时更新）

原文：https://www.cnblogs.com/talk-sea/p/14723699.html