正弦信号
\(A：幅度；\omega_0=\frac{2\pi}{T_0}：基波频率；\phi：相位\)
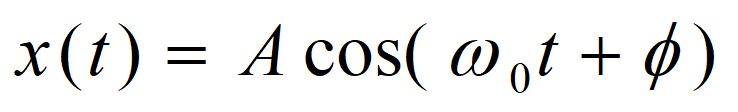意义：
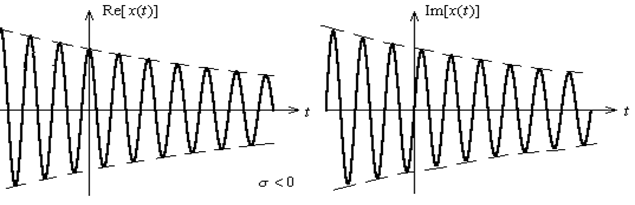
指数信号
，
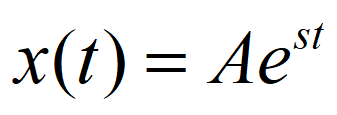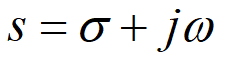
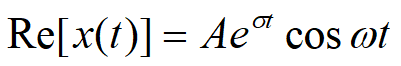
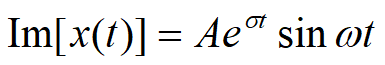
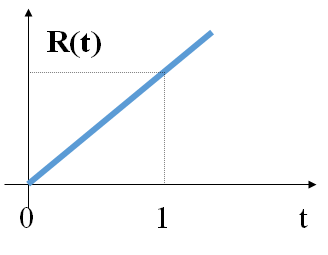
奇异信号：函数本身或者其导数含有不连续的点
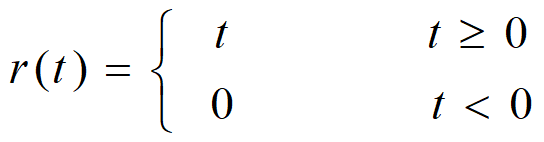
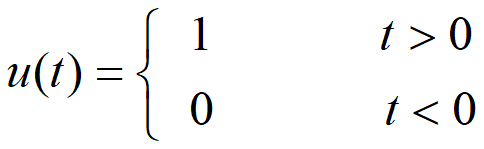
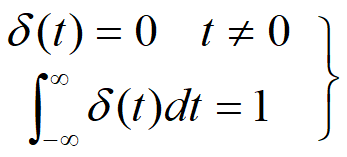
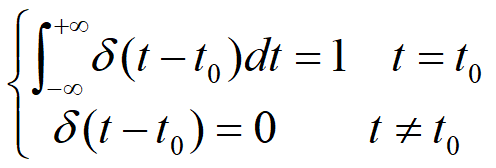
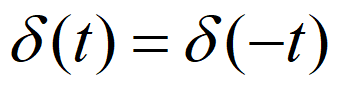
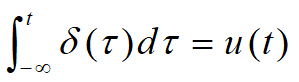
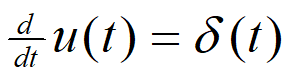
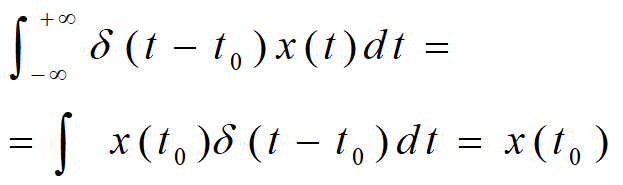
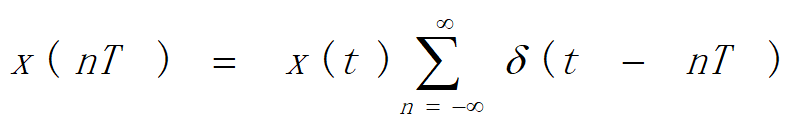
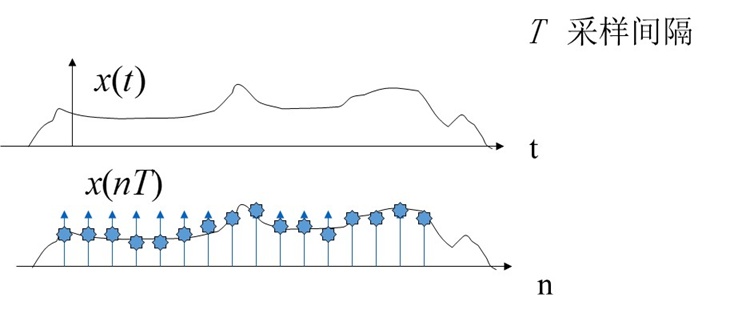
幅度尺度变换、时间尺度变换、翻转、平移
结果信号瞬时值为两个信号在该瞬时的值的代数和或乘积
信号的微分是指取信号对时间的一阶导数，表示为
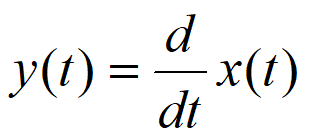
信号的积分是指信号\(x(t)\)在区间\((-\infty,t)\)内积分得到的信号，即
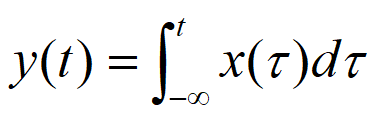
对于两个连续时间信号\(x_1(t)\)和\(x_2(t)\)，有
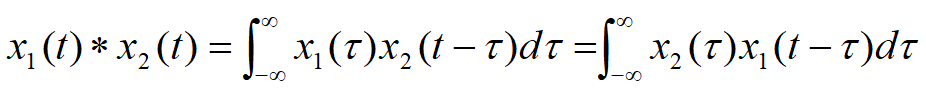
易得
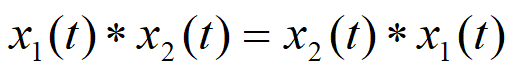
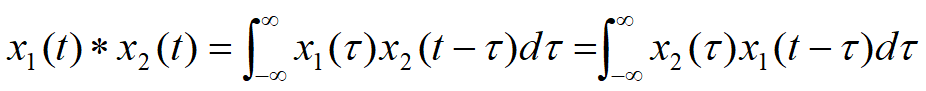
周期为T0的周期信号x(t)，如果满足狄里赫利条件，都可以分解成三角函数表达式：
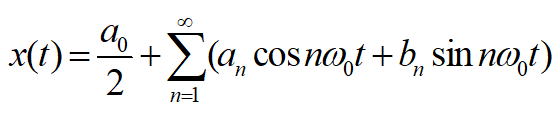其中,周期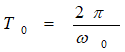
直流分量\(\frac{a_0}{2}\), 基波分量\(n=1\), 谐波分量 \(n> 1\)
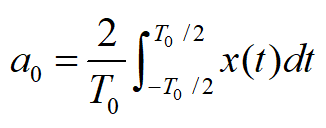
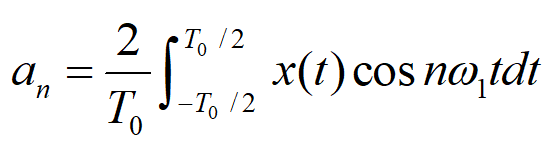
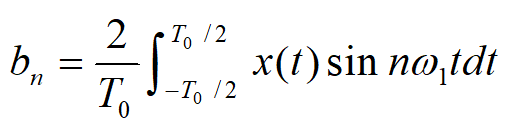
狄利赫利条件
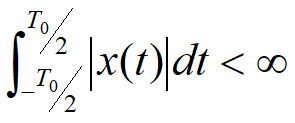
通常周期信号都满足这些条件
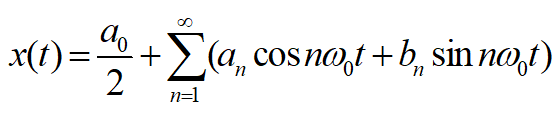$$
\Downarrow完备正交函数集
$$
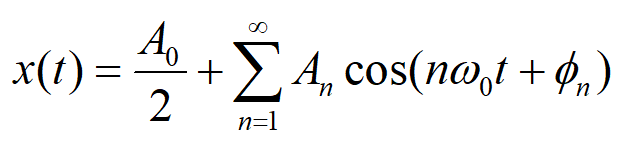
有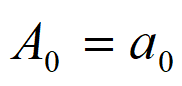
，
，
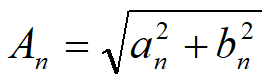周期信号可以分解为一系列余弦信号之和：
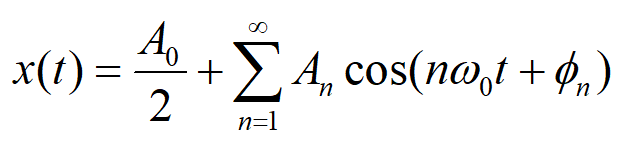
?表明一个周期为T0的信号，除直流分量外，包含有频率为原信号频率以及原信 号频率的整数倍的一系列正弦型信号，分别将它们称为基波信号（n=1,也称为一次谐波信号）, 二次谐波信号（n=2）,以及三次、四次……谐波信号，它们的振幅分别为对应的\(A_n\)，相位为\(\varphi_n.\)
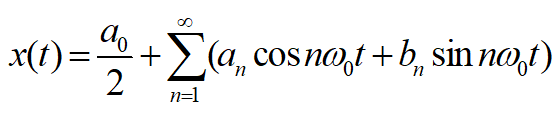\(\longrightarrow\)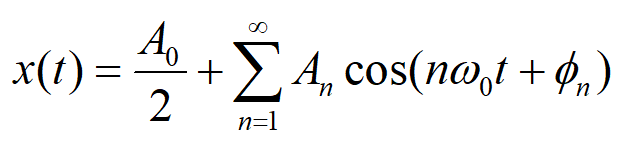
复数形式：区分开载频部分\(\longrightarrow\)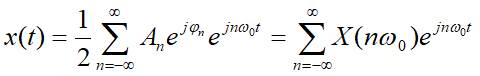
\(\longrightarrow\)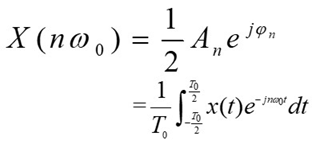
(重点关注包络)
指数形式的傅立叶级数表达式中复数量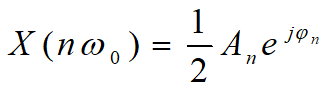
随频率的分布称为信号的频谱，也称为周期信号的频谱函数。
由于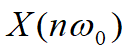 
包含了幅度和相位的分布，通常把幅度
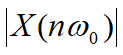随频率的分布称为幅度频谱，相位
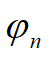随频率的分布称为相位频谱。
采（取）样函数
形如
的函数，记为\(Sa(x)\).
\(Sa(x)\)是偶函数，当\(x\to0\)时，\(Sa(x)=1\)为最大值，随着\(|x|\)的增大而总趋势衰减，\(x=\pm n\pi(n=1,2,3\cdots)\)为过零点，每\(2\pi\)起伏一次。
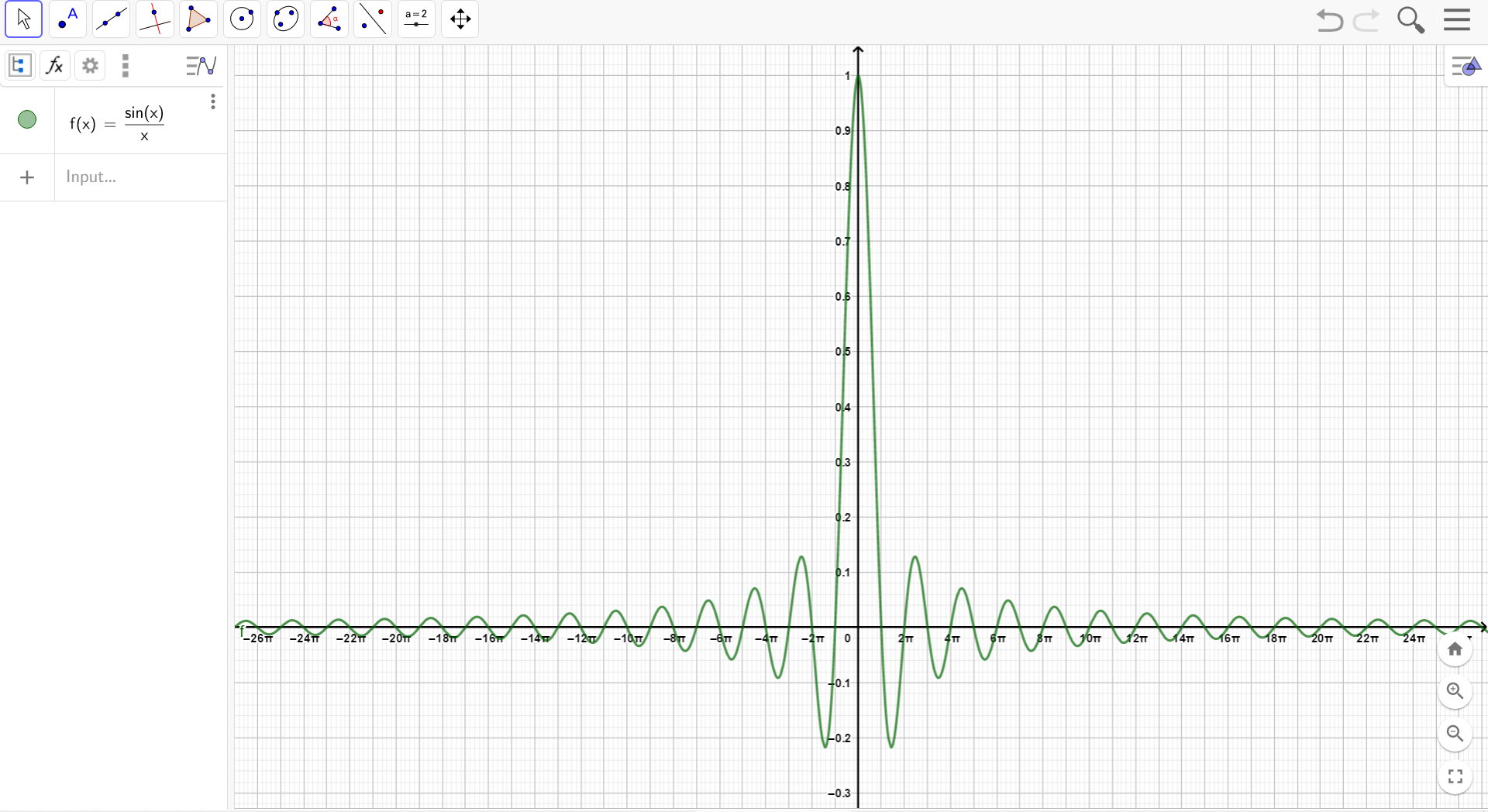
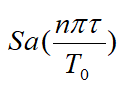为频谱的包络线，过零点为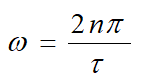 
以上三个特点是任何满足狄里赫利条件的周期信号的频谱所共同具有的特征
周期信号的谱线只出现在基波频率的整数倍的频率处
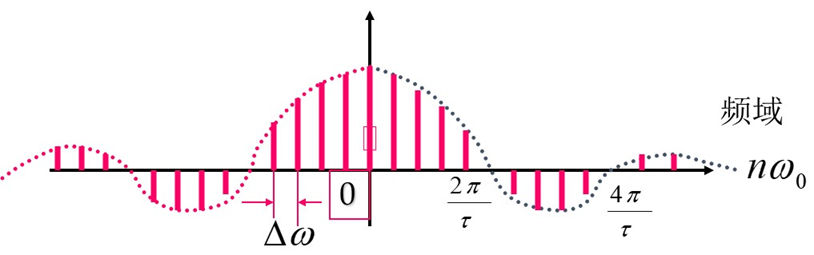
周期矩形脉冲的频谱随周期的变化而变化的关系
当脉冲宽度\(\pmb{\tau}\)保持不变,增大周期\(T_0\)
- 离散谱线的间隔
变小,即:谱线变得更加密集
- 各谱线的幅度
的增大而变小,包络线变化缓慢，即振幅收敛速度变慢
思考:若\(T_0\to\infty\),谱线会如何变化?
P为周期信号的平均功率，其中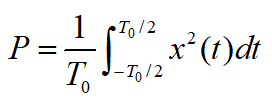
，代入\(x（t）\)的表达式：
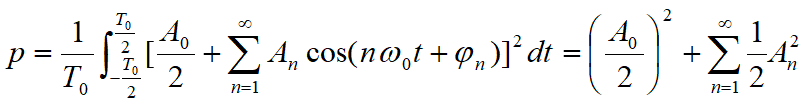
周期信号在时域的平均功率等于频域各分量的的平均功率之和
一般情况下一个周期信号是由无穷多项正弦型信号（直流、基波及各项谐波）组合而成，换言之，一般情况下，无穷多项正弦型信号的和才能完全逼近一个周期信号。 工程上，忽略高频能量，采用有限项级数表示周期信号，部分误差可忽略。
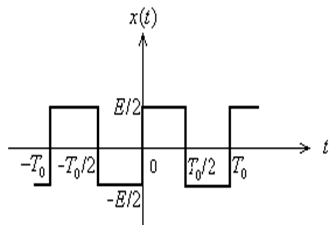
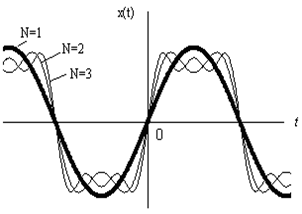
1.傅立叶级数所取项数越多，叠加后波形越逼近原信号，两者之间的均方误差越小
2.当信号为方波等脉冲信号时，其高频分量主要影响脉冲的跳变沿，低频分量主要影响脉冲的顶部。所以，波形变化愈激烈，所包含的高频分量愈丰富； 变化愈缓慢，所包含的低频分量愈丰富
3.组成原信号的任一频谱分量（包括幅值、相位）发生变化时，信号的波形也会发生变化
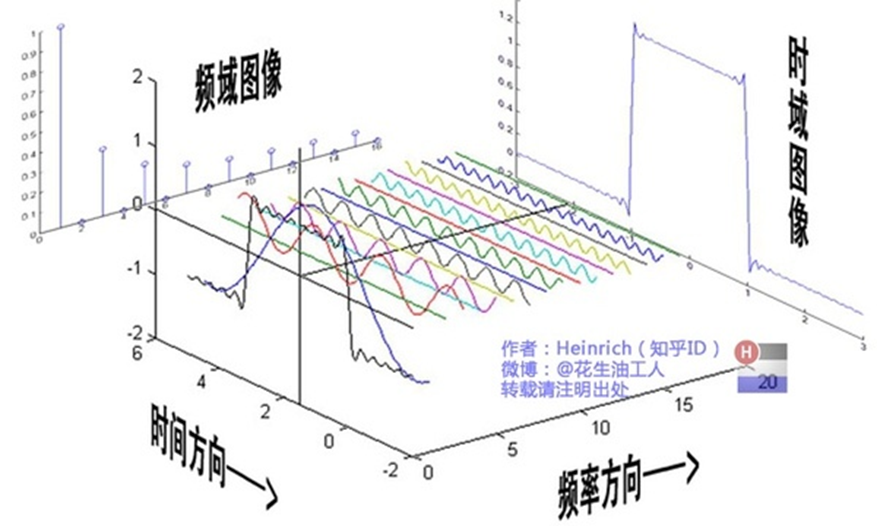
当周期矩形脉冲信号的周期\(T_0\)无限大时,就演变成了非周期的单脉冲信号，谱线无限密集，频率也变成连续变量
存在条件（狄里赫利条件）：
?在无限区间内是绝对可积的，即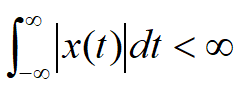
?在任意有限区间内，x(t)只有有限个不连续点，在这些点上函数取有限值。
?在任意有限区间内， x(t)只有有限个极大值和极小值。
从周期信号FS推导非周期的FT：
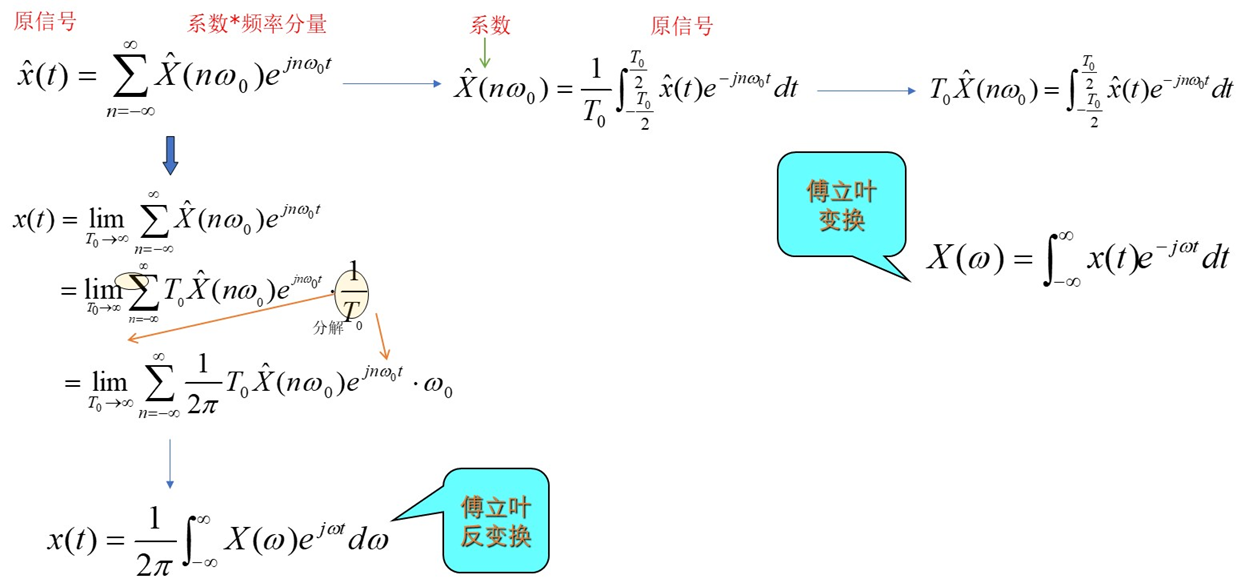
从物理意义来讨论傅立叶变换：
X(ω)是一个连续谱
X(ω)包含了从零到无限高频率的所有频率分量
各频率分量的频率不成谐波关系
X(ω)是一个频谱密度函数的概念
为什么叫频谱密度?
- 因为能量信号能量有限，并分布在连续的频谱轴上，所以在每个频点\(f\)信号的幅度是无穷小，只有在一小段频率间隔\(df\)上才有确定的非零振幅。所以，能量信号的每个频点的幅度都是0，------只有频谱密度才有意义。
- 检查下量纲：由傅里叶变换的公式得\(x(t)\)在时间维上的积分，量纲应该是\(伏特V*秒s = V/Hz\)，所以傅里叶变换的结果是频谱密度 。 而傅里叶级数则只有\(V\)(因为除以了\(T_0\))
只要引入冲激函数，我们同样可以求出一个功率信号的频谱密度，换句话说，引用了冲激函数就能把频谱密度推广到功率信号上，即我们可以直接对功率信号做傅里叶变换。这样把傅里叶变换的结果统称为频谱（严格来说应该是频谱密度）。
变换：
级数：
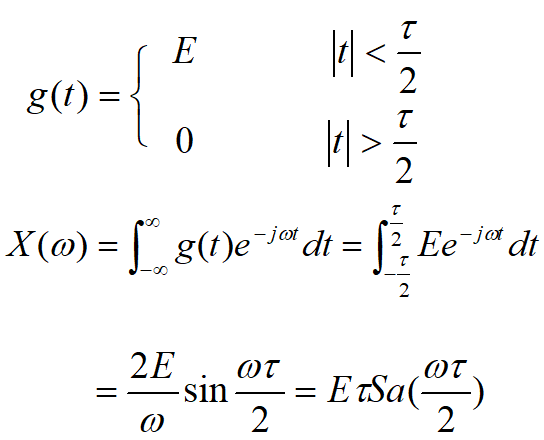
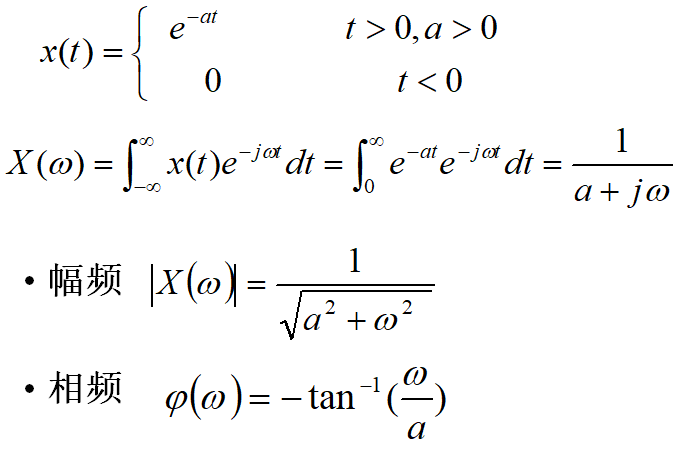
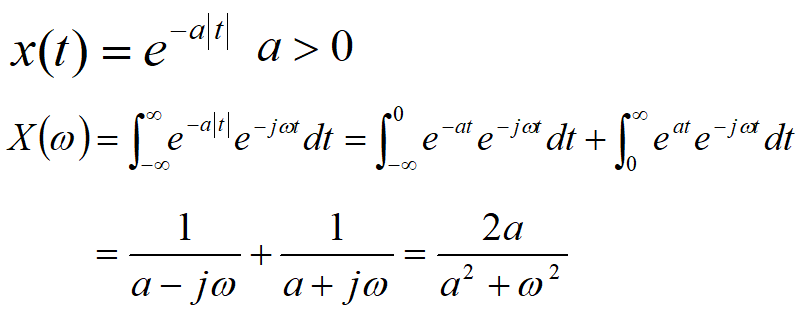
但再回想一下信号系统中最常见的正弦信号，这是个功率信号，但我们平时好像一直在说它的傅里叶变换，也并没有什么太大问题。这是因为引入了单位冲击函数
功率信号在某些频率上的功率密度为无穷大---可以用冲击函数来表示这些频率分量
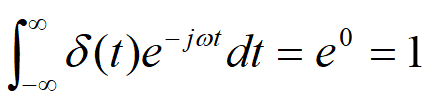
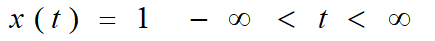
问题：功率信号(能量无穷大)不满足可以积条件,为啥可以求傅里叶变换？
因为引入了单位冲击函数。例如该信号所有能量集中在 0 频率上
功率信号在某些频率上的功率密度为无穷大---可以用冲击函数来表示这些频率分量，如：
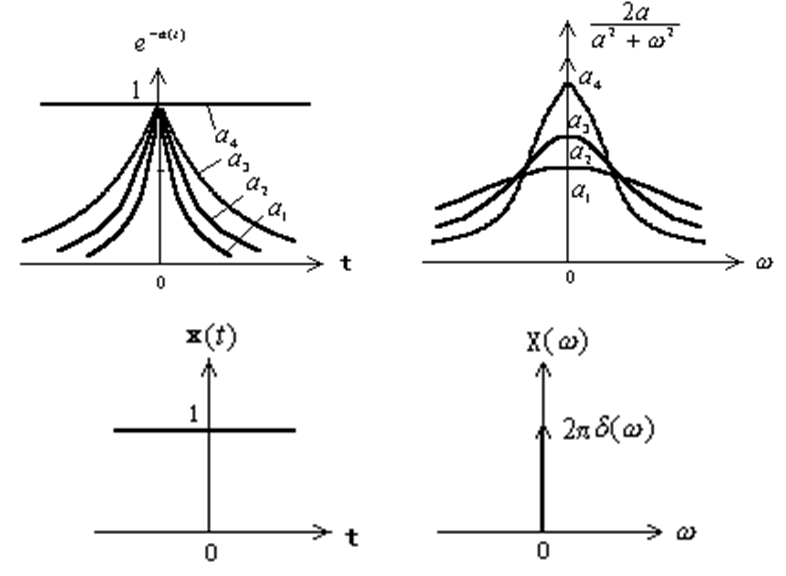
| 信号\(x(t)\) | 傅里叶变换\(X(\omega)\) |
|---|---|
| \(\delta(t)\) | \(1\) |
| \(\delta(t-t_0)\) | \(e^{-j\omega t_0}\) |
| \(1\) | \(2\pi\delta(\omega)\) |
| \(u(t)\) | \(\pi\delta(\omega)+\frac{1}{j\omega}\) |
| \(sgn(t)\) | \(\frac{2}{j\omega}\) |
| \(e^{-at}u(t)\quad a>0,a\in R\) | \(\frac{1}{j\omega+a}\) |
| \(g(t)=\begin{cases}1\quad &\vert t\vert<\frac{\tau}{2}\\ 0\quad&\vert t\vert>\frac{\tau}{2} \end{cases}\) | \(\tau Sa(\frac{\omega\tau}{2})\) |
| \(Sa(\omega_c t)\) | \(\frac{\pi}{\omega_c}g(\omega),g(\omega)=\begin{cases}1\quad &\vert \omega\vert<\omega_c\\ 0\quad&\vert \omega\vert>\omega_c \end{cases}\) |
| \(e^{-a\vert t\vert}\quad a>0\) | \(\frac{2a}{\omega^2+a^2}\) |
| \(e^{-(at)^2}\) | \(\frac{\sqrt{\pi}}{a}e^{-(\frac{\omega}{2a})^2}\) |
| \(e^{j\omega_0t}\) | \(2\pi\delta(\omega-\omega_0)\) |
| \(\cos\omega_0t\) | \(\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]\) |
| \(\sin\omega_0t\) | \(j\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)]\) |
| \(te^{-at}u(t)\quad a>0,a\in R\) | \(\frac{1}{(j\omega+a)^2}\) |
| \(\frac{t^{n-1}}{(n-1)!}e^{-at}u(t) \quad a>0,a\in R\) | \(\frac{1}{(j\omega+a)^n}\) |
| \(e^{-at}\cos\omega_0t\cdot u(t)\quad a>0\) | \(\frac{j\omega+a}{(j\omega+a)^2+\omega^2_0}\) |
| \(e^{-at}\sin\omega_0t\cdot u(t)\quad a>0\) | \(\frac{\omega_0}{(j\omega+a)^2+\omega^2_0}\) |
| \(\delta_r(t)=\sum\limits^\infty_{n=-\infty}\delta(t-nT_0)\) | \(\omega_0\sum\limits^\infty_{n=-\infty}\delta(\omega-n\omega_0)\quad\omega=\frac{2\pi}{T_0}\) |
| \(x(t)=\sum\limits^\infty_{n=-\infty}X(n\omega_0)e^{jn\omega_0t}\) | \(2\pi\sum\limits^\infty_{n=-\infty}X(n\omega_0)\delta(\omega-n\omega_0)\) |
| 性质 | 时域\(x(t)\) | 频域\(X(\omega)\) |
|---|---|---|
| 定义 | \(x(t)=\frac{1}{2\pi}\int^\infty_{-\infty}X(\omega)e^{j\omega t}d\omega\) | \(X(\omega)= \int^\infty_{-\infty}x(t)e^{-j\omega t}dt\\ \quad \quad\ =\vert X(\omega)\vert e^{j\varphi(\omega)}\\ \quad\quad\ =Re(\omega)+jIm(\omega)\) |
| 线性 | \(x_1(t)\stackrel{\mathscr{F}}{\longleftrightarrow}X_1(\omega)\\ x_2(t)\stackrel{\mathscr{F}}{\longleftrightarrow}X_2(\omega)\\ a_1x_1(t)+a_2x_2(t)\) | \(a_1X_1(\omega)+a_2X_2(\omega)\) |
| 奇偶性 | \(x^*(t)\\ 若x(t)为实函数, 即x(t)=x^*(t)\\ \ \\ \ \\ \ \\ \ \\ \ \\ x(t)为实偶函数x(t)=x(-t)\\x(t)为实奇函数x(t)=-x(-t)\) | \(X^*(-\omega)\\ X(\omega)=X^*(-\omega)或X^*(\omega)=X(-\omega)\\ \vert X(\omega)\vert=\vert X(-\omega)\vert\\ \varphi(\omega)=-\varphi(-\omega)\\ Re(\omega)=Re(-\omega)\\ Im(\omega)=-Im(-\omega)\\ X(\omega)=Re(\omega)\quad Im(\omega)=0\\ X(\omega)=jIm(\omega)\quad Re(\omega)=0\) |
| 对偶性 | \(X(t)\) | \(2\pi x(-\omega)\) |
| 尺度变换 | \(x(at)\quad a\not=0\) | \(\frac{1}{\vert a\vert}X(\frac{\omega}{a})\) |
| 翻转 | \(x(-t)\) | \(X(-\omega)\) |
| 时移 | \(x(t\pm t_0)\\ x(at-b)\quad a\not=0\) | \(e^{\pm j\omega t_0}X(\omega)\\ \frac{1}{\vert a\vert}X(\frac{\omega}{a})e^{-j\frac{b}{a}\omega}\) |
| 频移 | \(x(t)e^{\pm j\omega_0t}\) | \(X(\omega\mp\omega_0)\) |
| 时域微分 | \(\frac{d^n x(t)}{dt^n}\) | \((j\omega)^n X(\omega)\) |
| 时域积分 | \(\int^t_{-\infty}x(\tau)d\tau\) | \(\frac{1}{j\omega}X(\omega)+\pi X(0)\delta(\omega)\quad \color{red}X(0)\not=0\) |
| 帕斯瓦尔公式 | \(\int^\infty_{-\infty}\vert x(t)\vert^2 dt \quad(=)\) | \(\frac{1}{2\pi}\int^\infty_{-\infty}\vert X(\omega)\vert^2d\omega\) |
| 时域卷积 | \(x_1(t)^*x_2(t)\) | \(X_1(\omega)X_2(\omega)\) |
| 频域卷积 | \(x_1(t)x_2(t)\) | \(\frac{1}{2\pi}X_1(\omega)^*X_2(\omega)\) |
| 频域微分 | \(-jtx(t)\) | \(\frac{dX(\omega)}{d\omega}\) |
尺度变换特性说明：
在时域上将信号压缩到\(\frac{1}{|a|}\)倍，则在频域上其频谱扩展\(|a|\)倍，同时幅度相应地减小到\(\frac{1}{|a|}\)倍。也就是说，信号波形在时域的压缩意味着在频域中信号频带的展宽；反之，信号波形在时域的扩展，意味着频域中信号频带的压缩
在数字通信技术中，必须压缩矩形脉冲的宽度以提高通信速率，这时须展宽信道的频带。通信速度和占用频带宽度是一对矛盾
带有尺度变换的时移特性举例
单矩形脉冲\(f_0(t)\)的频谱为\(F_0(\omega)=E\tau Sa(\frac{\omega\tau}{2})\)，有如下三脉冲信号：
\[f(t)=f_0(t)+f_0(t+T)+f_0(t-T) \]其频谱为：
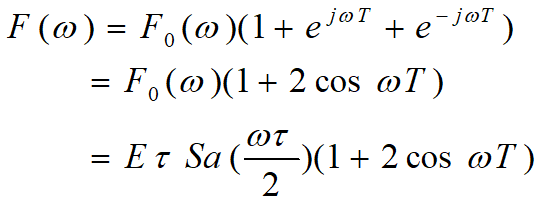
调幅信号的频谱（信号调制技术）（\(\bigstar\bigstar\)）
通信中常用的频谱搬移技术：上变频&下变频
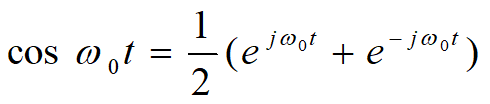
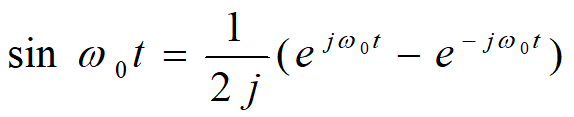
依据上面两式，可得：
信号的微分运算,对应频域乘上jw因子，增强高频部分 （例如图像的边沿检测）
积分（求和）实际上是增强了低频部分，减少了高频；积分注意初始条件
帕斯瓦尔定理表明，信号的总能量也可由频域求得
时域卷积应用：求三角脉冲的频谱
频域卷积应用：导出频移特性
\[\mathscr{F}[x(t)e^{j\omega_0t}]=\frac{1}{2\pi}X(\omega)*2\pi\delta(\omega-\omega_0)\X(\omega)*\delta(\omega-\omega_0)=X(\omega-\omega_0) \]任意信号与冲激函数\(\delta(t)\)的卷积是自身；与\(\delta(t-t_0)\)的卷积等效于原信号延迟
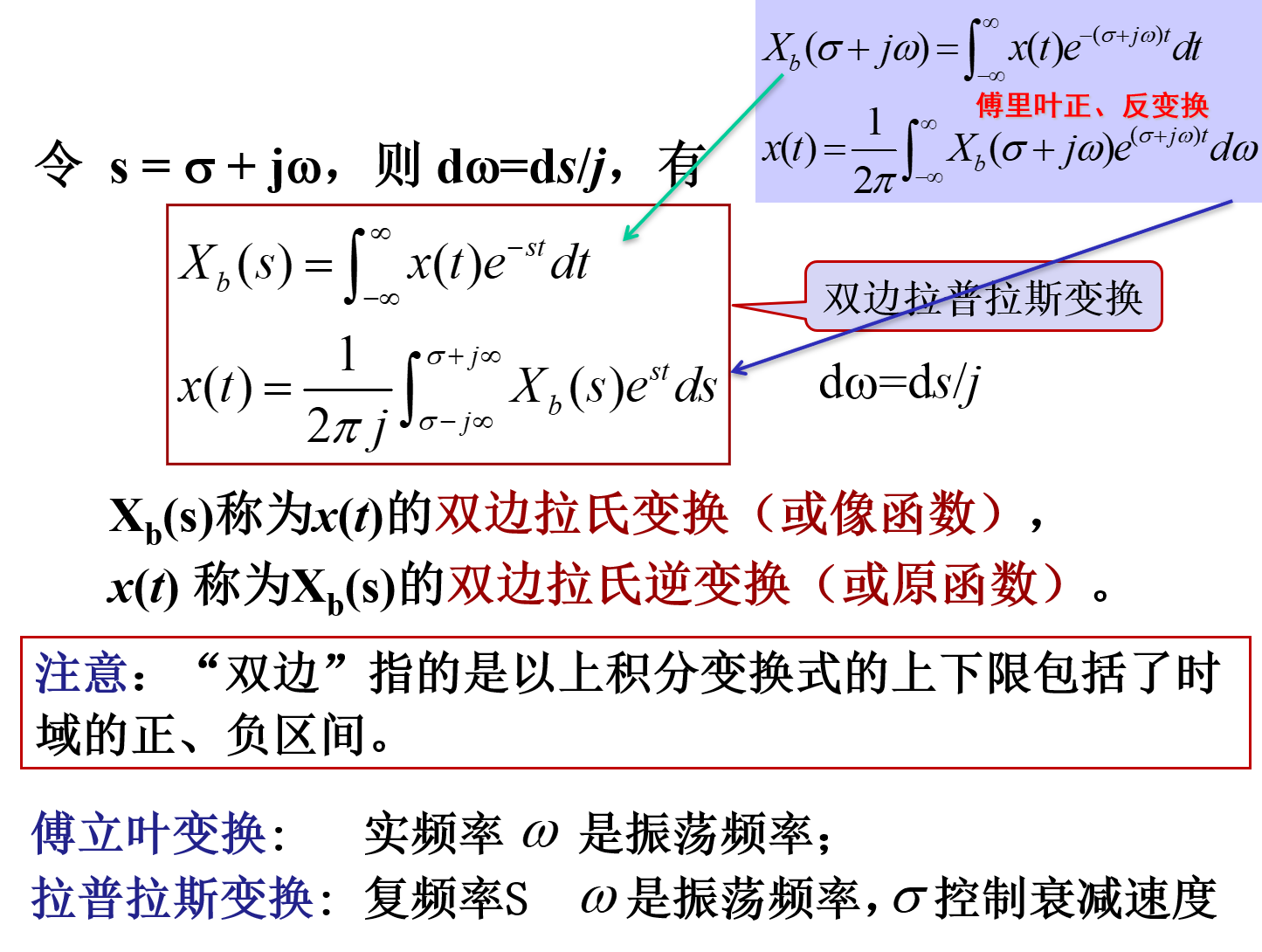
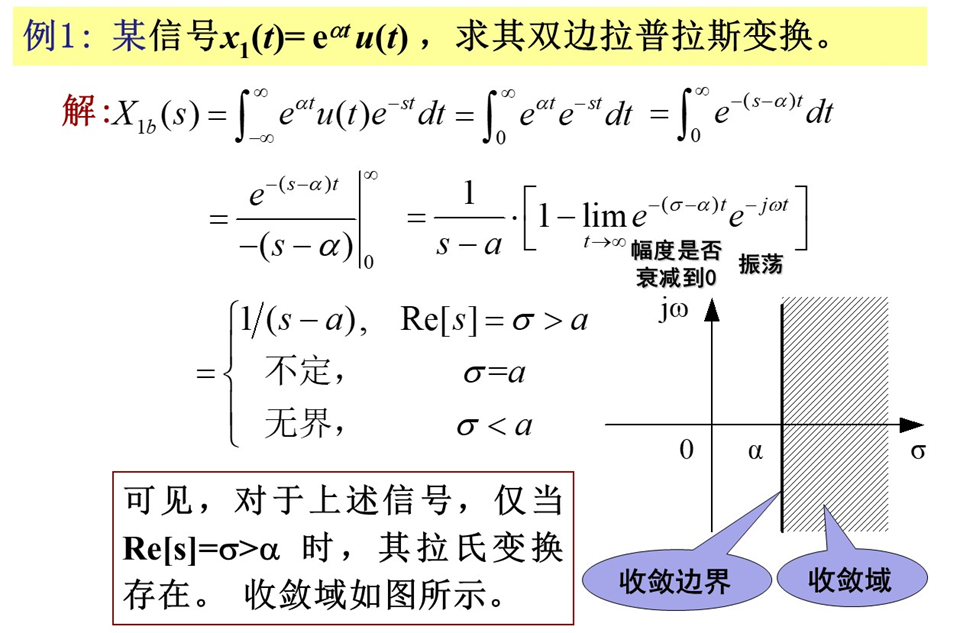
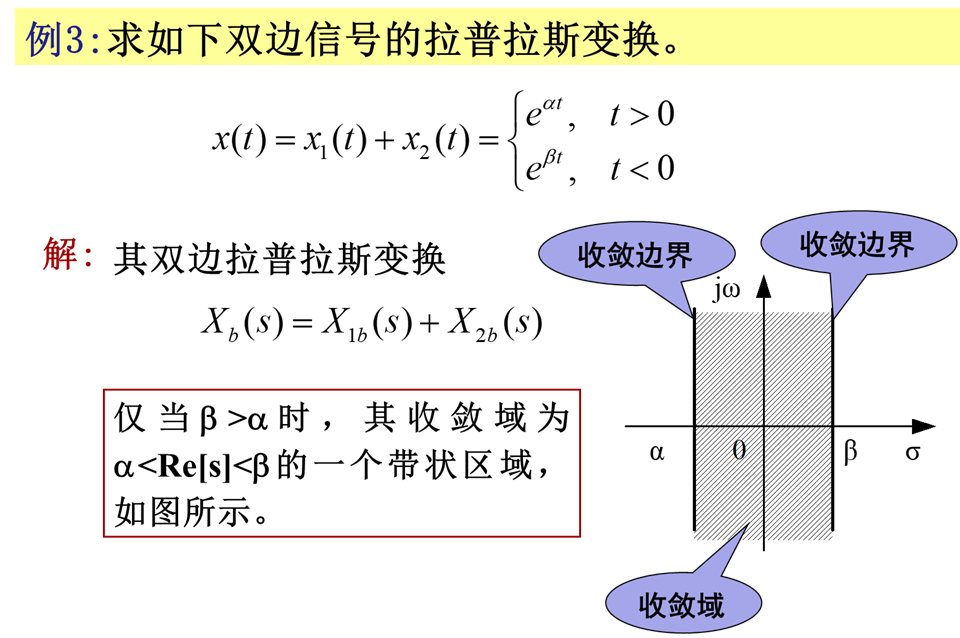
原文：https://www.cnblogs.com/WuDaijie2001/p/AnyTask_SAAP_003.html
