爱因斯坦求和(einsum),计算指定维度元素的乘积,再求和。可以将爱因斯坦求和记法理解为懒人求和记法,省略不写 \(\Sigma\)。einsum 具有很强大的表达能力,使用 einsum 的表达式,可以表达各种各样的操作,比如矩阵乘法、矩阵转置。很多库都支持 einsum,有 numpy,pytorch,tensorflow。
这篇文章分为三个部分。
下面以 pytorch 为例子,介绍 einsum 的一些常见的用法。
矩阵乘法中,每个元素由下面的表达式确定。
第一个学习的 einsum 表达式是,ik,kj->ij。前面提到过,爱因斯坦求和记法可以理解为懒人求和记法。将上述公式中的 \(\Sigma\) 去掉,并且将左右两边对调一下,省去矩阵之后,剩下的就是 ik,kj->ij 了。
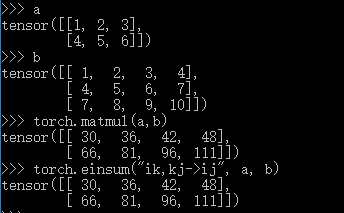
虽然 einsum 的名字当中有 sum,但是 einsum 可以不做求和。举个例子,获取二维方阵的对角线元素,结果放入一维向量。
上面,A 是一维向量,B 是二维方阵。使用 einsum 记法,可以写作 ii->i
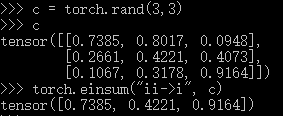
观察一下,矩阵乘法和对角线元素两个表达式有什么区别。ik,kj->ij 和 ii->i。
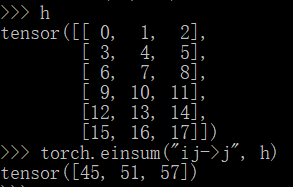
k 而箭头右边没有。i。基于上面的观察,可以大致推测出来,左边出现但是右边没有出现的符号,这个符号省略了 \(\Sigma\)。
接下来,我们来尝试一下求解矩阵的迹(trace),即对角线元素的和。
t 是常量,A 是二维方阵。按照前面的做法,省略 \(\Sigma\),左右两边对调,省去矩阵和 t,剩下的就是 kk->。
对,你没有看错,右边没有东西。这意味着,左边的符号都省略了 \(\Sigma\)。
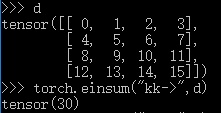
有了前面的基础,矩阵转置就很简单啦,写表达式。
A 和 B 都是二维方阵。einsum 可以表达为 ij->ji。
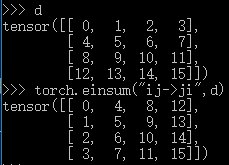
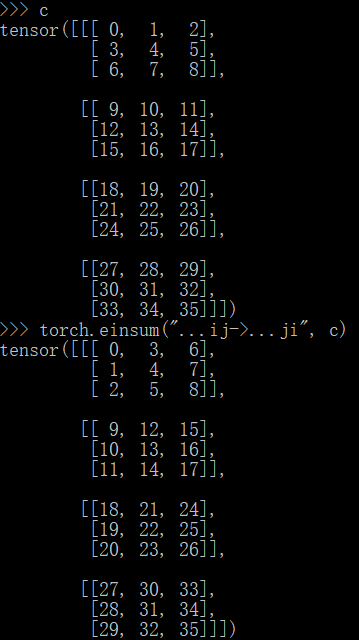
在 pytorch 中,还支持省略前面的维度。比如,只转置最后两个维度,可以表达为 ...ij->...ji。下面展示了一个含有四个二维矩阵的三维矩阵,转置三维矩阵中的每个二维矩阵。
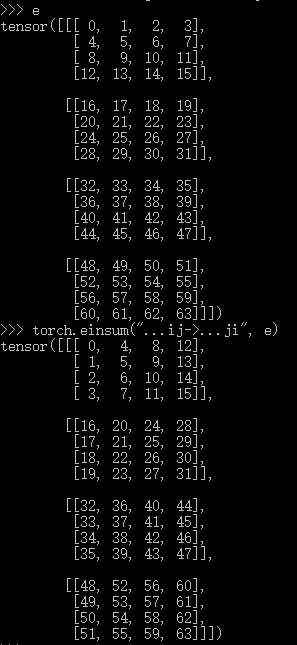
在快速上手了 einsum 之后,接下来考察一下 einsum,补充一些细节。
pytorch 的文档写得非常清楚了:https://pytorch.org/docs/stable/generated/torch.einsum.html
下面总结一下规则:
ij->jiba 完整的表达式是 ba->abkj,ji 完整的表达式是 kj,ji->ik,矩阵乘法再相乘。ab->aa 是非法的,ab->c 是非法的,ab->a 是合法的。... 是用来跳过部分维度。例子,...ij,...jk 表示 batch 矩阵乘法。b...a 完整的表达式是 b...a->...ab,可以将一个形状为 (a,b,c) 的矩阵变为形状为 (b,c,a) 的矩阵。i,i,i 表示将三个一维向量按位相乘,并相加。i j , j k -> ik 是合法的,ij,jk - > ik 是非法的。(4,3,3) 的矩阵,表达式 ab->a 是非法的,abc-> 是合法的。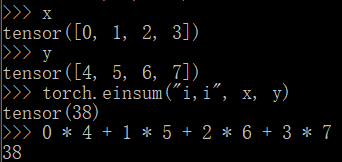
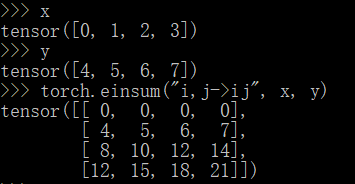
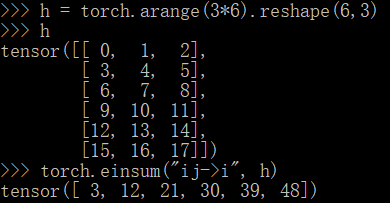
上面简单介绍了 einsum 的用法,einsum 可以表达很多操作,比如矩阵乘法、矩阵转置。上面仅仅是做了简单的介绍,大家在炼丹的过程中,遇到过哪些让你直呼牛逼的 einsum 表达式呢?希望能得到你的分享,感谢!
原文:https://www.cnblogs.com/zzk0/p/14723925.html