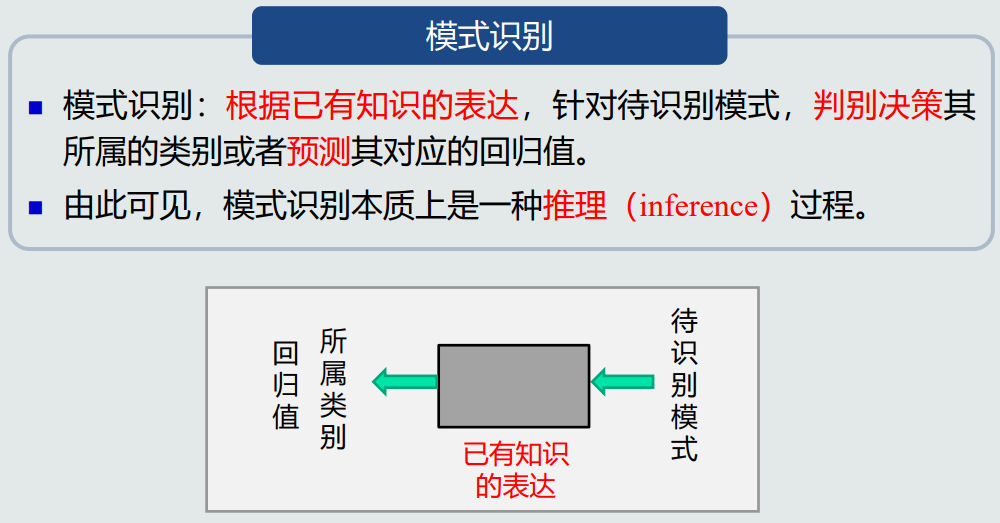
模型是指关于已有知识的一种表达方式,即函数f(x)。
二类分类判别器使用sign函数:判断回归值大于0还是小于0。
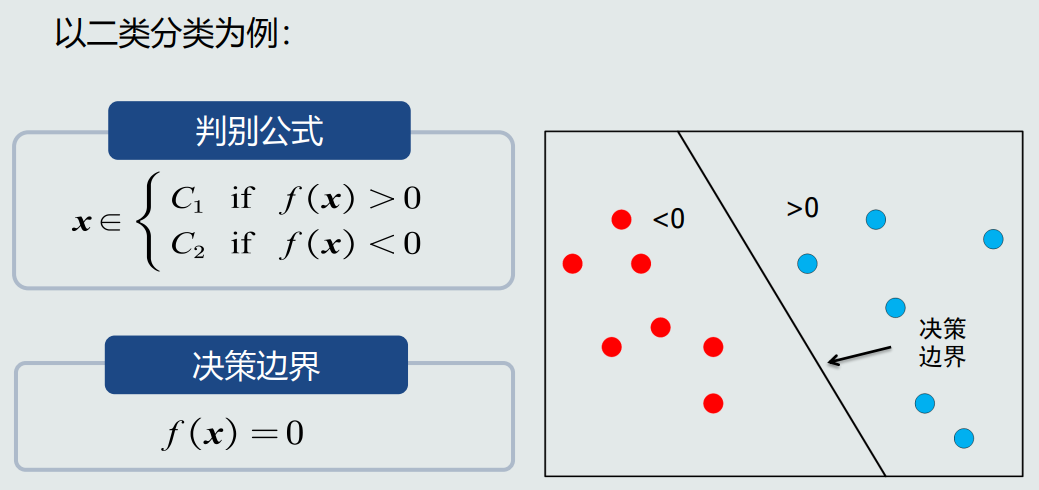
多类分类判别器使用max函数,取最大的回归值所在维度对应的类别。
特征向量指多个特征构成的(列)向量。

训练样本可认为是尚未加工的原始知识,模型则是经过学习后的真正知识表达。
线性模型(直线、面、超平面)。
非线性模型(曲线、曲面、超曲面)。
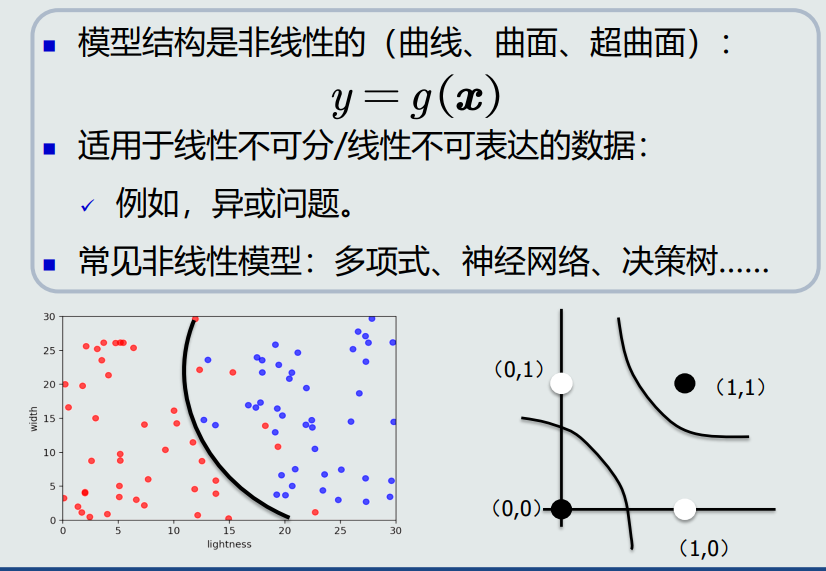
常见非线性模型:多项式、神经网络、决策树……
监督式学习:训练样本极其输出真值都给定情况下的机器学习算法。
无监督式学习:只给定训练样本、没有输出真值情况下的机器学习算法。
半监督式学习:既有标注的训练样本、又有未标注的训练样本情况下的学习算法。
强化学习:机器自行探索决策,真值滞后反馈的过程。
泛化能力:学习算法对新模式的决策能力。
训练集是模型训练所用的样本数据,集合中的每个样本称作训练样本;测试集是测试模型性能所用的样本数据,集合中的每个样本称作测试样本。
测试样本假设从样本真实分布中独立同分布(iid)。
测试误差也称泛化误差。
过拟合是泛化能力低的表现。
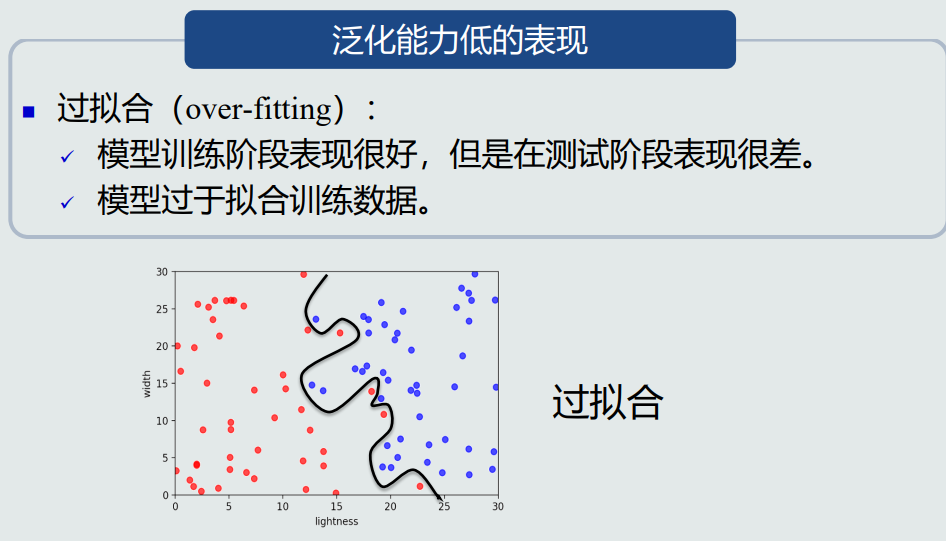
提高泛化能力的一个思路是不要过度训练。
模型性能的评估方法通常有留出法、K折交叉验证、留一验证等。
准确度=(TP+TN)/(TP+TN+FP+FN)。
精度=TP/(TP+FP)。
召回率=TP/(TP+FN)。
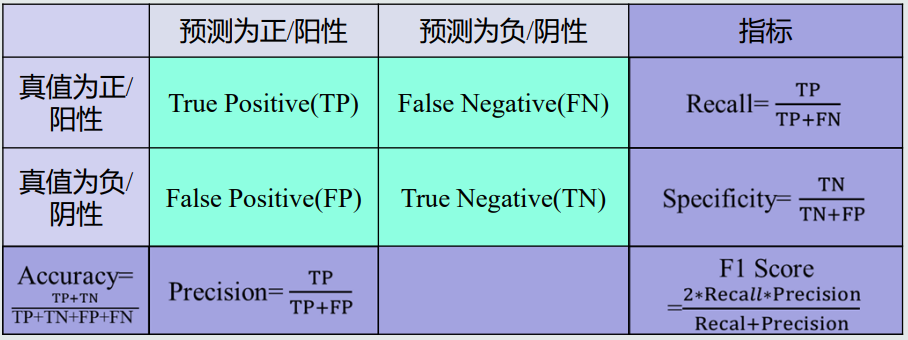
F-score=((a2+1)*精度*召回率)/(a2*精度+召回率),a为常数。
PR曲线:横轴召回率,纵轴精度。
ROC曲线:横轴为1-specificity,纵轴为召回率。
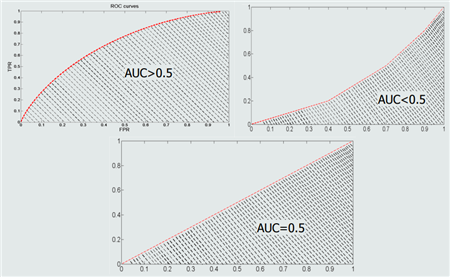
AUC:曲线下方面积。
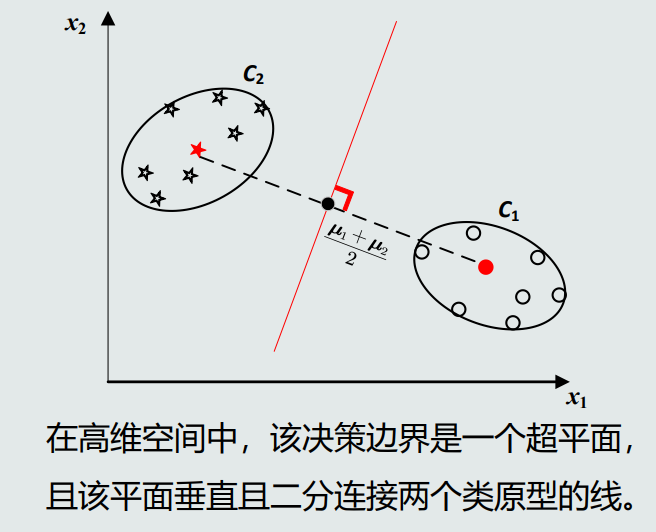
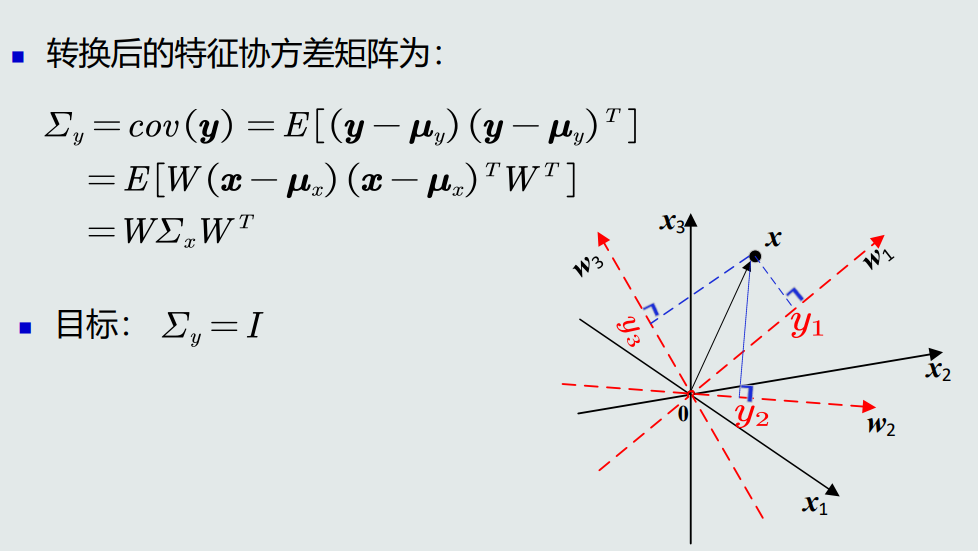
MICD分类器:最小类内距离分类器,基于马氏距离。
MICD分类器等距图是一个超球面/超椭圆面(高维空间)。
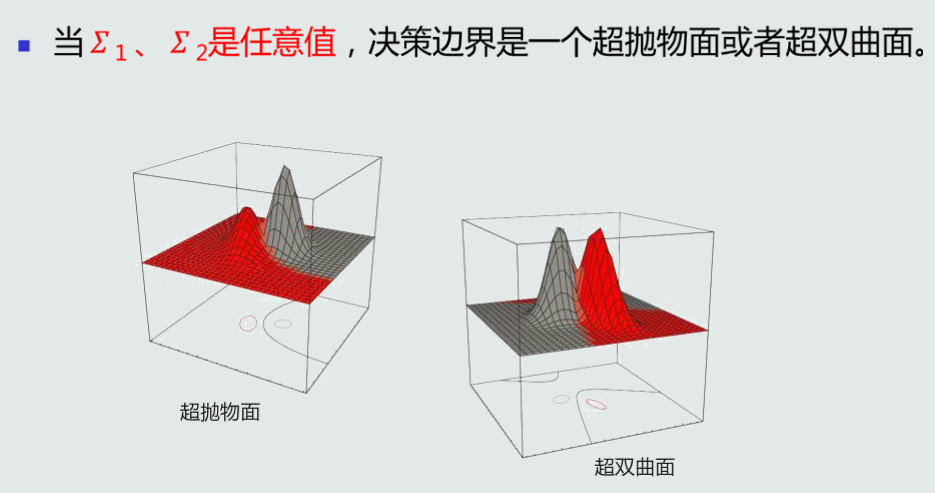
MICD分类器决策边界可是一个超抛物面或者超双曲面。
MICD的缺陷:选择方差较大的类。
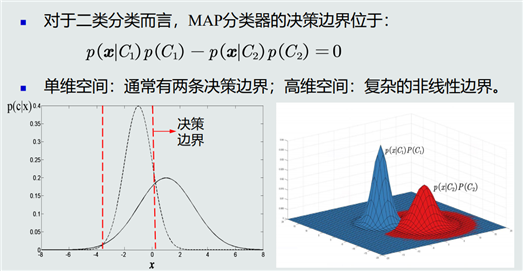
MAP分类器:最大后验概率分类器,将测试样本决策分类给后验概率最大的那个类。
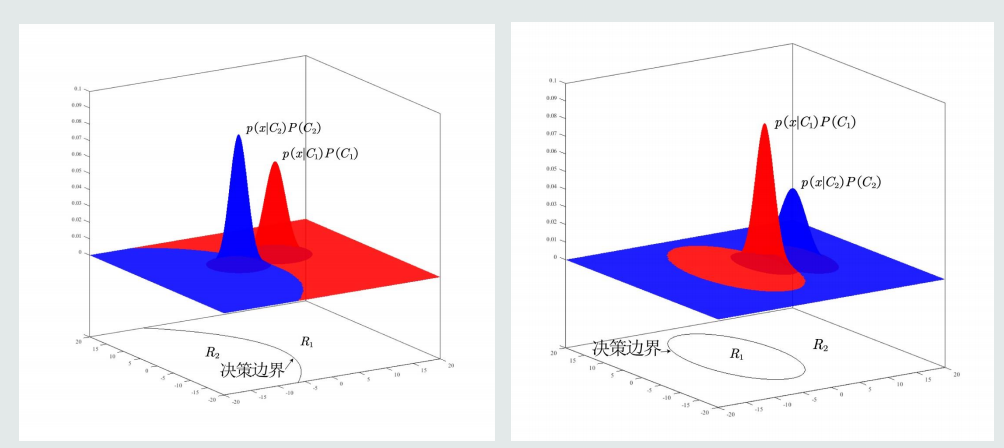
单维空间MAP分类器通常有两类决策边界,高维空间决策边界是复杂的非线性边界。
MAP分类器决策目标:最小化概率误差。
不同的错误决策会产生程度完全不一样的风险。

贝叶斯分类器:在MAP分类器的基础上,加入决策风险因素。
贝叶斯分类器的决策目标:最小化期望损失。
如果特征是多维,学习特征之间的相关性会很困难。朴素贝叶斯分类器假设特征之间是相互独立的。
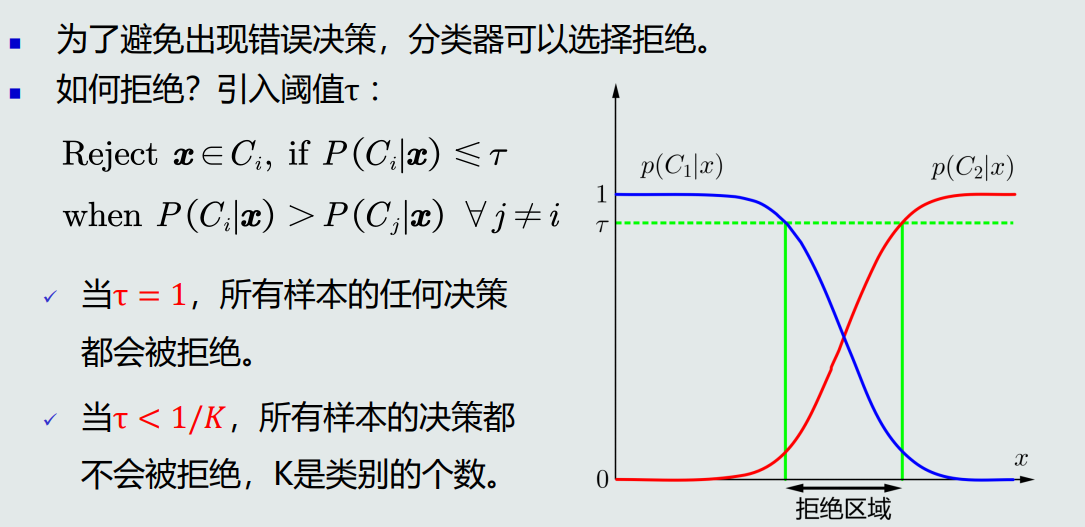
为了避免出现错误决策,分类器可以选择拒绝,可以通过引入阈值的方法实现。
先验概率的最大似然估计就是该类训练样本出现的频率。
高斯分布均值的最大似然估计等于样本的均值。

高斯分布协方差的最大似然估计等于所有训练模式的协方差。
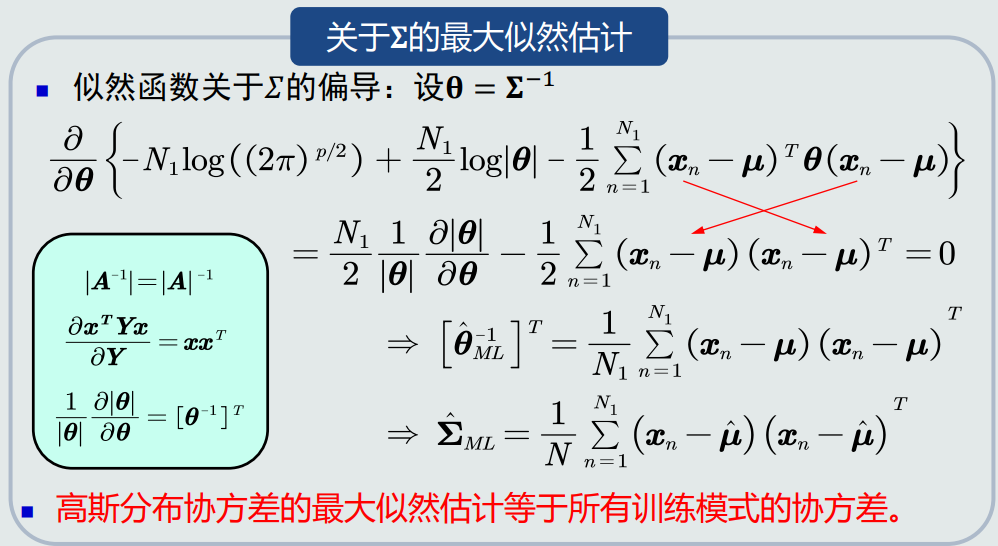
高斯分布均值的最大似然估计是无偏估计。

高斯分布协方差的最大似然估计是有偏估计。


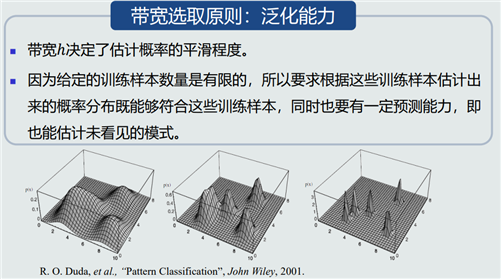
如果概率分布形式未知,可以通过无参数技术来实现概率密度估计。常用的无参数技术主要有K近邻法、直方图技术、核密度估计等。
KNN估计:K近邻估计,给定x,找到其对应的区域R使其包含k个训练样本,以此计算p(x)。
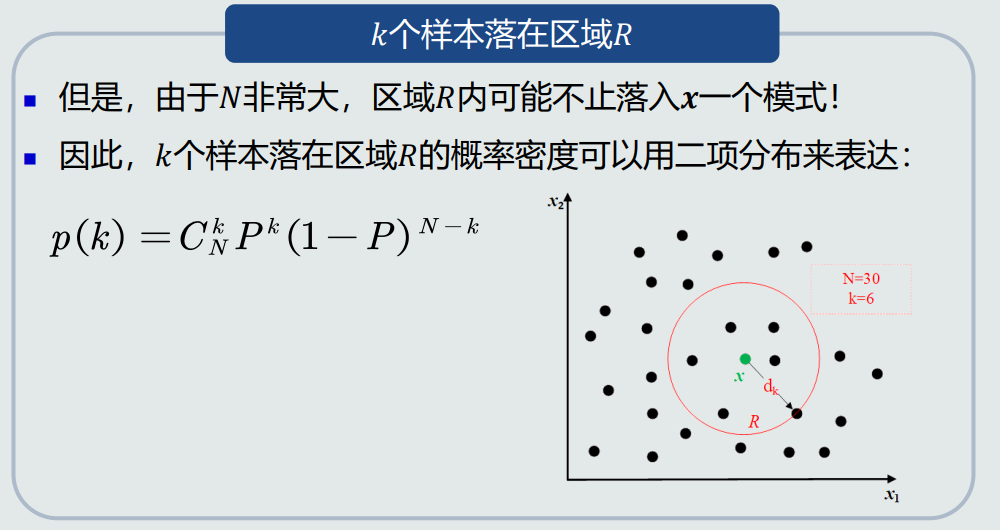
KNN优点:可以自适应地确定x相关的区域R的范围。缺点:KNN概率密度估计不是连续函数;不是真正的概率密度表达,概率密度函数积分是无穷而不是1。
KNN估计的问题:仍然需要存储所有训练样;易受噪声影响。
直方图的概率密度也是不连续的。
直方图估计优点:减少由于噪声污染造成的估计误差;不需要存储训练样本。缺点:估计可能不准确;缺乏概率估计的自适应能力。

核密度估计的核函数可以是高斯分布、均匀分布、三角分布等。

核密度估计优点:自适应确定区域R的位置;使用所有训练样本,克服KNN估计存在的噪声影响;如果核函数连续,则估计的概率密度函数也是连续的。缺点:必须要存储所有训练样本。
原文:https://www.cnblogs.com/Malancholy/p/14729305.html