题目一:
10000个正整数,编号1到10000,用A[1],A[2],A[10000]表示。
修改:无
统计:1.编号从L到R的所有数之和为多少? 其中1<= L <= R <= 10000.
方法一:对于统计L,R ,需要求下标从L到R的所有数的和,从L到R的所有下标记做[L..R],问题就是对A[L..R]进行求和。
这样求和,对于每个询问,需要将(R-L+1)个数相加。
方法二:更快的方法是求前缀和,令 S[0]=0, S[k]=A[1..k] ,那么,A[L..R]的和就等于S[R]-S[L-1],
这样,对于每个询问,就只需要做一次减法,大大提高效率。
题目二:
10000个正整数,编号从1到10000,用A[1],A[2],A[10000]表示。
修改:1.将第L个数增加C (1 <= L <= 10000)
统计:1.编号从L到R的所有数之和为多少? 其中1<= L <= R <= 10000.
再使用方法二的话,假如A[L]+=C之后,S[L],S[L+1],,S[R]都需要增加C,全部都要修改,见下表。

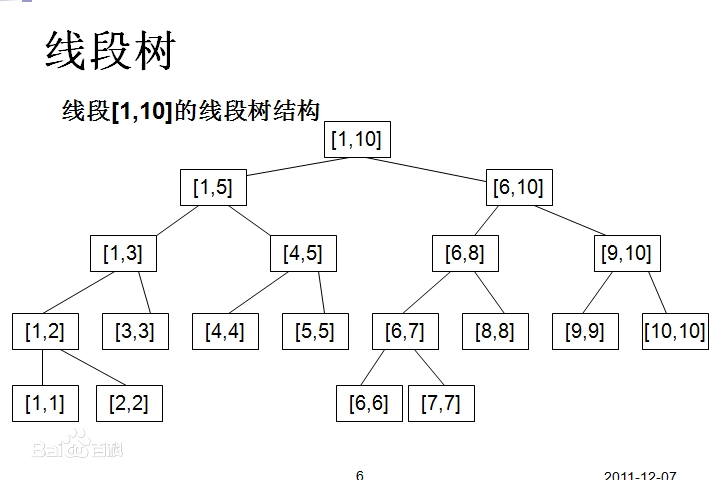
上面的问题二就是典型的线段树点修改。线段树先将区间[1..10000]分成不超过4*10000个子区间,对于每个子区间,记录一段连续数字的和。之后,任意给定区间[L,R],线段树在上述子区间中选择约2*log2(R-L+1)个拼成区间[L,R]。如果A[L]+=C ,线段树的子区间中,约有log2(10000)个包含了L,所以需要修改log2(10000)个。于是,使用线段树的话,A[L]+=C 需要修改log2(10000) 个元素求和A[L...R]需要修改2*log2(R-L+1) <= 2 * log2(10000) 个元素。log2(10000) < 14 所以相对来说线段树的修改和求和都比较快。
线段树是一种二叉树,当然可以像一般的树那样写成结构体,指针什么的。但是它的优点是,它也可以用数组来实现树形结构,可以大大简化代码。数组形式适合在编程竞赛中使用,在已经知道线段树的最大规模的情况下,直接开足够空间的数组,然后在上面建立线段树。简单的记法: 足够的空间 = 数组大小n的四倍。实际上足够的空间 = (n向上扩充到最近的2的某个次方)的两倍。举例子:假设数组长度为5,就需要5先扩充成8,8*2=16.线段树需要16个元素。如果数组元素为8,那么也需要16个元素。所以线段树需要的空间是n的两倍到四倍之间的某个数,一般就开4*n的空间就好,如果空间不够,可以自己算好最大值来省点空间。
怎么用数组来表示一颗二叉树呢?假设某个节点的编号为v,那么它的左子节点编号为2*v,右子节点编号为2*v+1。然后规定根节点为1.这样一颗二叉树就构造完成了。通常2*v在代码中写成 v<<1 。 2*v+1写成 v<<1|1 。
(1)建树:
1 /** 2 * 构造线段树 3 * @param arr 存储1~n的连续正整数的数组 4 * @param tree 用于存储构成的线段树的数组(利用满二叉树的形式顺序存储) 5 * @param root 根节点编号(编号从1开始) 6 * @param start 左区间(同上) 7 * @param end 右区间(同上) 8 */ 9 public static void buildSegTree(int[] arr, int[] tree, int root, int start, int end) { 10 if (start >= end) { 11 tree[root - 1] = arr[start - 1]; 12 return; 13 } 14 15 int mid = (start + end) / 2; 16 // 左孩子 17 int left_root = root * 2; 18 // 右孩子 19 int right_root = root * 2 + 1; 20 // 递归 21 buildSegTree(arr, tree, left_root, start, mid); 22 buildSegTree(arr, tree, right_root, mid + 1, end); 23 // 更新 24 tree[root - 1] = tree[left_root - 1] + tree[right_root - 1]; 25 }
(2)点修改:
1 /** 2 * 修改线段树 3 * 时间复杂度:O(log(n)) 4 * @param arr 存储1~n的连续正整数的数组 5 * @param tree 用于存储构成的线段树的数组(利用满二叉树的形式顺序存储) 6 * @param root 根节点编号(编号从1开始) 7 * @param start 左区间(同上) 8 * @param end 右区间(同上) 9 * @param pos 要修改的位置 10 * @param val 要修改后的值 11 */ 12 public static void updateSegTree(int[] arr, int[] tree, int root, int start, int end, int pos, int val) { 13 if (start >= end) { 14 if (start == pos) { 15 arr[start - 1] = val; 16 tree[root - 1] = val; 17 } 18 return; 19 } 20 21 int mid = (start + end) / 2; 22 int left_root = root * 2; 23 int right_root = root * 2 + 1; 24 updateSegTree(arr, tree, left_root, start, mid, pos, val); 25 updateSegTree(arr, tree, right_root, mid + 1, end, pos, val); 26 // 更新 27 tree[root - 1] = tree[left_root - 1] + tree[right_root - 1]; 28 }
(3)区间查询(本题为求和):
1 /** 2 * 查询线段树中区间[L, R] 3 * 时间复杂度:O(log(n)) 4 * @param arr 存储1~n的连续正整数的数组 5 * @param tree 用于存储构成的线段树的数组(利用满二叉树的形式顺序存储) 6 * @param root 根节点编号(编号从1开始) 7 * @param start 左区间(同上) 8 * @param end 右区间(同上) 9 * @param L 区间左边界 10 * @param R 区间右边界 11 */ 12 public static int querySegTree(int[] arr, int[] tree, int root, int start, int end, int L, int R) { 13 // 处理三种特殊情况 14 if (R < start || L > end) { 15 // 不相交 16 return 0; 17 } 18 if (L <= start && R >= end) { 19 // 包含 20 return tree[root - 1]; 21 } 22 if (start >= end) { 23 // 只有一个元素,直接返回 24 return arr[start - 1]; 25 } 26 27 int mid = (start + end) / 2; 28 int left_root = root * 2; 29 int right_root = root * 2 + 1; 30 int leftSum = querySegTree(arr, tree, left_root, start, mid, L, R); 31 int rightSum = querySegTree(arr, tree, right_root, mid + 1, end, L, R); 32 return leftSum + rightSum; 33 }
1 package com.lzp.util; 2 3 import java.util.Arrays; 4 5 /** 6 * @Author LZP 7 * @Date 2021/5/5 10:04 8 * @Version 1.0 9 * 10 * 线段树 11 */ 12 public class SegmentTree { 13 14 /** 15 * 构造线段树 16 * @param arr 存储1~n的连续正整数的数组 17 * @param tree 用于存储构成的线段树的数组(利用满二叉树的形式顺序存储) 18 * @param root 根节点编号(编号从1开始) 19 * @param start 左区间(同上) 20 * @param end 右区间(同上) 21 */ 22 public static void buildSegTree(int[] arr, int[] tree, int root, int start, int end) { 23 if (start >= end) { 24 tree[root - 1] = arr[start - 1]; 25 return; 26 } 27 28 int mid = (start + end) / 2; 29 // 左孩子 30 int left_root = root * 2; 31 // 右孩子 32 int right_root = root * 2 + 1; 33 // 递归 34 buildSegTree(arr, tree, left_root, start, mid); 35 buildSegTree(arr, tree, right_root, mid + 1, end); 36 // 更新 37 tree[root - 1] = tree[left_root - 1] + tree[right_root - 1]; 38 } 39 40 /** 41 * 修改线段树 42 * 时间复杂度:O(log(n)) 43 * @param arr 存储1~n的连续正整数的数组 44 * @param tree 用于存储构成的线段树的数组(利用满二叉树的形式顺序存储) 45 * @param root 根节点编号(编号从1开始) 46 * @param start 左区间(同上) 47 * @param end 右区间(同上) 48 * @param pos 要修改的位置 49 * @param val 要修改后的值 50 */ 51 public static void updateSegTree(int[] arr, int[] tree, int root, int start, int end, int pos, int val) { 52 if (start >= end) { 53 if (start == pos) { 54 arr[start - 1] = val; 55 tree[root - 1] = val; 56 } 57 return; 58 } 59 60 int mid = (start + end) / 2; 61 int left_root = root * 2; 62 int right_root = root * 2 + 1; 63 updateSegTree(arr, tree, left_root, start, mid, pos, val); 64 updateSegTree(arr, tree, right_root, mid + 1, end, pos, val); 65 // 更新 66 tree[root - 1] = tree[left_root - 1] + tree[right_root - 1]; 67 } 68 69 /** 70 * 查询线段树中区间[L, R] 71 * 时间复杂度:O(log(n)) 72 * @param arr 存储1~n的连续正整数的数组 73 * @param tree 用于存储构成的线段树的数组(利用满二叉树的形式顺序存储) 74 * @param root 根节点编号(编号从1开始) 75 * @param start 左区间(同上) 76 * @param end 右区间(同上) 77 * @param L 区间左边界 78 * @param R 区间右边界 79 */ 80 public static int querySegTree(int[] arr, int[] tree, int root, int start, int end, int L, int R) { 81 // 处理三种特殊情况 82 if (R < start || L > end) { 83 // 不相交 84 return 0; 85 } 86 if (L <= start && R >= end) { 87 // 包含 88 return tree[root - 1]; 89 } 90 if (start >= end) { 91 // 只有一个元素,直接返回 92 return arr[start - 1]; 93 } 94 95 int mid = (start + end) / 2; 96 int left_root = root * 2; 97 int right_root = root * 2 + 1; 98 int leftSum = querySegTree(arr, tree, left_root, start, mid, L, R); 99 int rightSum = querySegTree(arr, tree, right_root, mid + 1, end, L, R); 100 return leftSum + rightSum; 101 } 102 103 public static void main(String[] args) { 104 int n = 8; 105 int[] arr = new int[n]; 106 for (int i = 0; i < n; i++) { 107 arr[i] = i + 1; 108 } 109 // 线段树 110 // 线段树先将区间[1..n]分成不超过4*n个子区间,对于每个子区间,记录一段连续数字的和。 111 int[] tree = new int[4 * n + 10]; 112 buildSegTree(arr, tree, 1, 1, n); 113 System.out.println("建树之后:" + Arrays.toString(tree)); 114 115 updateSegTree(arr, tree, 1, 1, n, 4, 5); 116 System.out.println("修改之后:" + Arrays.toString(tree)); 117 118 // 原本2~7之和为27,但是由于前面已经修改过(把4改成5),所以区间[2, 7]之和为28 119 int left = 2; 120 int right = 7; 121 int result = querySegTree(arr, tree, 1, 1, n, left, right); 122 System.out.printf("区间[%d, %d] = %d\n", left, right, result); 123 } 124 }

原文:https://www.cnblogs.com/pengsay/p/14731282.html