


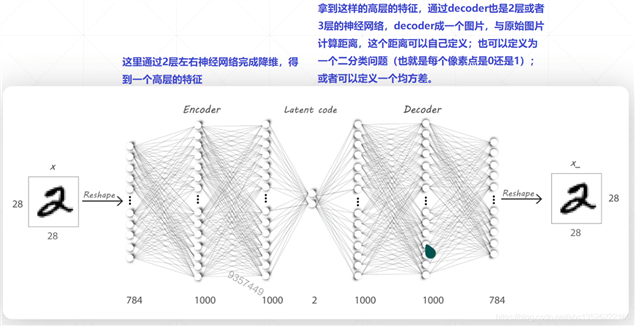
import os import numpy as np import tensorflow as tf from tensorflow import keras from PIL import Image from matplotlib import pyplot as plt from tensorflow.keras import Sequential, layers tf.random.set_seed(22) np.random.seed(22) os.environ[‘TF_CPP_MIN_LOG_LEVEL‘] = ‘2‘ assert tf.__version__.startswith(‘2.‘) # 把多张image保存达到一张image里面去。 def save_images(img, name): new_im = Image.new(‘L‘, (280, 280)) index = 0 for i in range(0, 280, 28): for j in range(0, 280, 28): im = img[index] im = Image.fromarray(im, mode=‘L‘) new_im.paste(im, (i, j)) index += 1 new_im.save(name) # 定义超参数 h_dim = 20 # 把原来的784维护降低到20维度; batchsz = 512 # fashion_mnist lr = 1e-4 # 数据集加载 (x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data() x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255. # we do not need label auto-encoder大家可以理解为无监督学习,标签其实就是本身,和自己对比; train_db = tf.data.Dataset.from_tensor_slices(x_train) train_db = train_db.shuffle(batchsz * 5).batch(batchsz) test_db = tf.data.Dataset.from_tensor_slices(x_test) test_db = test_db.batch(batchsz) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) # 搭建模型 class AE(keras.Model): # 1. 初始化部分 def __init__(self): super(AE, self).__init__() # 调用父类的函数 # Encoders编码, 网络 self.encoder = Sequential([ layers.Dense(256, activation=tf.nn.relu), layers.Dense(128, activation=tf.nn.relu), layers.Dense(h_dim) ]) # Decoders解码,网络 self.decoder = Sequential([ layers.Dense(128, activation=tf.nn.relu), layers.Dense(256, activation=tf.nn.relu), layers.Dense(784) ]) # 2. 前向传播的过程 def call(self, inputs, training=None): # [b, 784] ==> [b, 10] h = self.encoder(inputs) # [b, 10] ==> [b, 784] x_hat = self.decoder(h) return x_hat # 创建模型 model = AE() model.build(input_shape=(None, 784)) # 注意这里面用小括号还是中括号是有讲究的。建议使用tuple model.summary() optimizer = keras.optimizers.Adam(lr=lr) # optimizer = tf.optimizers.Adam() 都可以; for epoch in range(1000): for step, x in enumerate(train_db): # [b, 28, 28] => [b, 784] x = tf.reshape(x, [-1, 784]).numpy() with tf.GradientTape() as tape: x_rec_logits = model(x) # 把每个像素点当成一个二分类的问题; rec_loss = tf.losses.binary_crossentropy(x, x_rec_logits, from_logits=True) # rec_loss = tf.losses.MSE(x, x_rec_logits) rec_loss = tf.reduce_mean(rec_loss) grads = tape.gradient(rec_loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) if step % 100 ==0: print(‘epoch: %3d, step:%4d, loss:%9f‘ %(epoch, step, float(rec_loss)))
if step % 100 ==0: print(‘epoch: %3d, step:%4d, loss:%9f‘ %(epoch, step, float(rec_loss))) ##################添加的代码################## # evaluation x = next(iter(test_db)) # 我们从test_db中取出一张图片; x_shape = tf.reshape(x, [-1, 784]).numpy() logits = model(x_shape) # 经过auto-encoder重建的效果。 x_hat= tf.sigmoid(logits) # 变化到0-1之间 # [b, 784] => [b, 28, 28] 还原成原始尺寸; x_hat = tf.reshape(x_hat, [-1, 28, 28]) # 重建得到的图片; # [b, 28, 28] => [2b, 28, 28] 和原图像拼接起来; x_concat = tf.concat([x, x_hat], axis=0) # 最外的维度拼接; x_concat = x_hat x_concat = x_concat.numpy() * 255. # 把数据numpy取出来,变成0-255区间; x_concat = x_concat.astype(np.uint8) # 还原成numpy保存图片的格式; save_images(x_concat, ‘ae_image/rec_epoch_%d.png‘ %epoch) # 每个epoch保存一次。
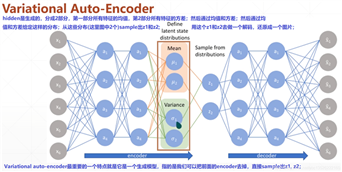
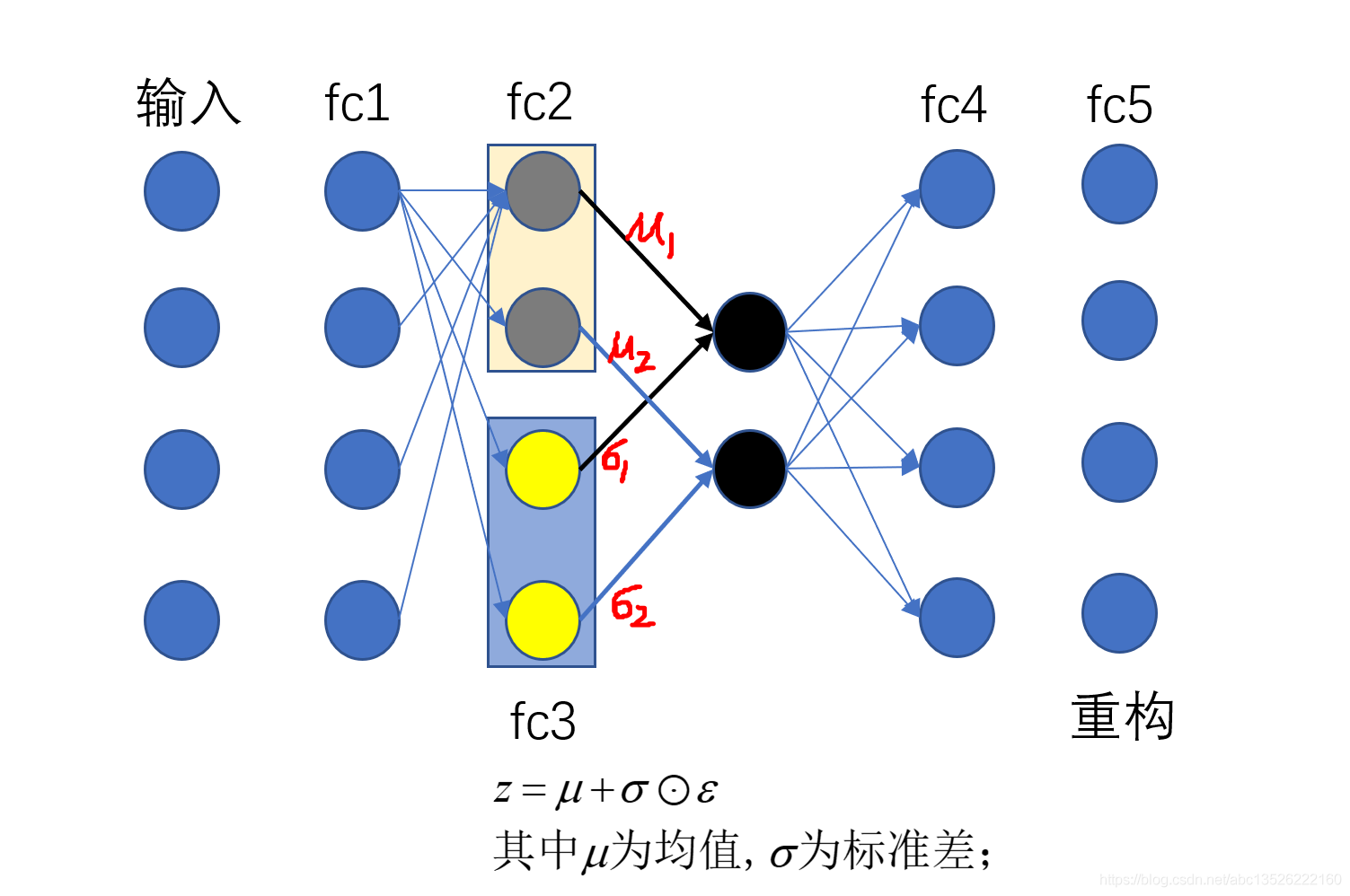
# 搭建模型 z_dim = 10 class VAE(keras.Model): def __init__(self): super(VAE, self).__init__() # Encoders编码, 网络 self.fc1 = layers.Dense(128, activation=tf.nn.relu) # 小网路1:均值(均值和方差是一一对应的,所以维度相同) self.fc2 = layers.Dense(z_dim) # get mean prediction # 小网路2 self.fc3 = layers.Dense(z_dim) # get mean prediction # Decoders解码,网络 self.fc4 = layers.Dense(128) self.fc5 = layers.Dense(784) # encoder传播的过程 def encoder(self, x): h = tf.nn.relu(self.fc1(x)) # get mean mu = self.fc2(h) # get variance log_var = self.fc3(h) return mu, log_var # 注意这里看成取了一个log函数; # decoder传播的过程 def decoder(self, z): out = tf.nn.relu(self.fc4(z)) out = self.fc5(out) return out def reparameterize(self, mu, log_var): eps = tf.random.normal(log_var.shape) var = tf.exp(log_var) # 去掉log, 得到方差; std = var**0.5 # 开根号,得到标准差; z = mu + std * eps return z def call(self, inputs, training=None): # [b, 784] => [b, z_dim], [b, z_dim] mu, log_var = self.encoder(inputs) # reparameterizaion trick:最核心的部分 z = self.reparameterize(mu, log_var) # decoder 进行还原 x_hat = self.decoder(z) # Variational auto-encoder除了前向传播不同之外,还有一个额外的约束;这个约束放在损失函数中; # 这个约束使得你的mu, var更接近正太分布;所以我们把mu, log_var返回; return x_hat, mu, log_var
注意:Variational auto-encoder 除了前向传播不同之外,还有一个额外的约束;这个约束放在损失函数中;这个约束使得你的 mu, var 更接近正太分布;所以我们把 mu, log_var 返回;
注意损失函数:

代码:
# compute kl divergence (mu, var) ~ N(0, 1): 我们得到的均值方差和正太分布的; # 链接参考: https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians kl_div = -0.5 * (log_var + 1 -mu**2 - tf.exp(log_var)) kl_div = tf.reduce_mean(kl_div) / batchsz # x.shape[0]
完整代码:
import os import tensorflow as tf from tensorflow import keras from PIL import Image from matplotlib import pyplot as plt from tensorflow.keras import Sequential, layers import numpy as np tf.random.set_seed(22) np.random.seed(22) os.environ[‘TF_CPP_MIN_LOG_LEVEL‘] = ‘2‘ assert tf.__version__.startswith(‘2.‘) # 把多张image保存达到一张image里面去。 def save_images(img, name): new_im = Image.new(‘L‘, (280, 280)) index = 0 for i in range(0, 280, 28): for j in range(0, 280, 28): im = img[index] im = Image.fromarray(im, mode=‘L‘) new_im.paste(im, (i, j)) index += 1 new_im.save(name) # 定义超参数 batchsz = 256 # fashion_mnist lr = 1e-4 # 数据集加载 (x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data() x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255. # we do not need label auto-encoder大家可以理解为无监督学习,标签其实就是本身,和自己对比; train_db = tf.data.Dataset.from_tensor_slices(x_train) train_db = train_db.shuffle(batchsz * 5).batch(batchsz) test_db = tf.data.Dataset.from_tensor_slices(x_test) test_db = test_db.batch(batchsz) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) # 搭建模型 z_dim = 10 class VAE(keras.Model): def __init__(self): super(VAE, self).__init__() # Encoders编码, 网络 self.fc1 = layers.Dense(128, activation=tf.nn.relu) # 小网路1:均值(均值和方差是一一对应的,所以维度相同) self.fc2 = layers.Dense(z_dim) # get mean prediction # 小网路2 self.fc3 = layers.Dense(z_dim) # get mean prediction # Decoders解码,网络 self.fc4 = layers.Dense(128) self.fc5 = layers.Dense(784) # encoder传播的过程 def encoder(self, x): h = tf.nn.relu(self.fc1(x)) # get mean mu = self.fc2(h) # get variance log_var = self.fc3(h) return mu, log_var # decoder传播的过程 def decoder(self, z): out = tf.nn.relu(self.fc4(z)) out = self.fc5(out) return out def reparameterize(self, mu, log_var): eps = tf.random.normal(log_var.shape) std = tf.exp(log_var) # 去掉log, 得到方差; std = std**0.5 # 开根号,得到标准差; z = mu + std * eps return z def call(self, inputs, training=None): # [b, 784] => [b, z_dim], [b, z_dim] mu, log_var = self.encoder(inputs) # reparameterizaion trick:最核心的部分 z = self.reparameterize(mu, log_var) # decoder 进行还原 x_hat = self.decoder(z) # Variational auto-encoder除了前向传播不同之外,还有一个额外的约束; # 这个约束使得你的mu, var更接近正太分布;所以我们把mu, log_var返回; return x_hat, mu, log_var model = VAE() model.build(input_shape=(128, 784)) optimizer = keras.optimizers.Adam(lr=lr) for epoch in range(100): for step, x in enumerate(train_db): x = tf.reshape(x, [-1, 784]) with tf.GradientTape() as tape: # shape x_hat, mu, log_var = model(x) # 把每个像素点当成一个二分类的问题; rec_loss = tf.losses.binary_crossentropy(x, x_hat, from_logits=True) # rec_loss = tf.losses.MSE(x, x_rec_logits) rec_loss = tf.reduce_mean(rec_loss) # compute kl divergence (mu, var) ~ N(0, 1): 我们得到的均值方差和正太分布的; # 链接参考: https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians kl_div = -0.5 * (log_var + 1 -mu**2 - tf.exp(log_var)) kl_div = tf.reduce_mean(kl_div) / batchsz # x.shape[0] loss = rec_loss + 1. * kl_div grads = tape.gradient(loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) if step % 100 ==0: print(‘epoch: %3d, step:%4d, kl_div: %5f, rec_loss:%9f‘ %(epoch, step, float(kl_div), float(rec_loss)))
测试代码:
import os import tensorflow as tf from tensorflow import keras from PIL import Image from matplotlib import pyplot as plt from tensorflow.keras import Sequential, layers import numpy as np tf.random.set_seed(22) np.random.seed(22) os.environ[‘TF_CPP_MIN_LOG_LEVEL‘] = ‘2‘ assert tf.__version__.startswith(‘2.‘) # 把多张image保存达到一张image里面去。 def save_images(img, name): new_im = Image.new(‘L‘, (280, 280)) index = 0 for i in range(0, 280, 28): for j in range(0, 280, 28): im = img[index] im = Image.fromarray(im, mode=‘L‘) new_im.paste(im, (i, j)) index += 1 new_im.save(name) # 定义超参数 batchsz = 256 # fashion_mnist lr = 1e-4 # 数据集加载 (x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data() x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255. # we do not need label auto-encoder大家可以理解为无监督学习,标签其实就是本身,和自己对比; train_db = tf.data.Dataset.from_tensor_slices(x_train) train_db = train_db.shuffle(batchsz * 5).batch(batchsz) test_db = tf.data.Dataset.from_tensor_slices(x_test) test_db = test_db.batch(batchsz) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) # 搭建模型 z_dim = 10 class VAE(keras.Model): def __init__(self): super(VAE, self).__init__() # Encoders编码, 网络 self.fc1 = layers.Dense(128, activation=tf.nn.relu) # 小网路1:均值(均值和方差是一一对应的,所以维度相同) self.fc2 = layers.Dense(z_dim) # get mean prediction # 小网路2 self.fc3 = layers.Dense(z_dim) # get mean prediction # Decoders解码,网络 self.fc4 = layers.Dense(128) self.fc5 = layers.Dense(784) # encoder传播的过程 def encoder(self, x): h = tf.nn.relu(self.fc1(x)) # get mean mu = self.fc2(h) # get variance log_var = self.fc3(h) return mu, log_var # decoder传播的过程 def decoder(self, z): out = tf.nn.relu(self.fc4(z)) out = self.fc5(out) return out def reparameterize(self, mu, log_var): eps = tf.random.normal(log_var.shape) std = tf.exp(log_var) # 去掉log, 得到方差; std = std**0.5 # 开根号,得到标准差; z = mu + std * eps return z def call(self, inputs, training=None): # [b, 784] => [b, z_dim], [b, z_dim] mu, log_var = self.encoder(inputs) # reparameterizaion trick:最核心的部分 z = self.reparameterize(mu, log_var) # decoder 进行还原 x_hat = self.decoder(z) # Variational auto-encoder除了前向传播不同之外,还有一个额外的约束; # 这个约束使得你的mu, var更接近正太分布;所以我们把mu, log_var返回; return x_hat, mu, log_var model = VAE() model.build(input_shape=(128, 784)) optimizer = keras.optimizers.Adam(lr=lr) for epoch in range(100): for step, x in enumerate(train_db): x = tf.reshape(x, [-1, 784]) with tf.GradientTape() as tape: # shape x_hat, mu, log_var = model(x) # 把每个像素点当成一个二分类的问题; rec_loss = tf.losses.binary_crossentropy(x, x_hat, from_logits=True) # rec_loss = tf.losses.MSE(x, x_rec_logits) rec_loss = tf.reduce_mean(rec_loss) # compute kl divergence (mu, var) ~ N(0, 1): 我们得到的均值方差和正太分布的; # 链接参考: https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians kl_div = -0.5 * (log_var + 1 -mu**2 - tf.exp(log_var)) kl_div = tf.reduce_mean(kl_div) / batchsz # x.shape[0] loss = rec_loss + 1. * kl_div grads = tape.gradient(loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) if step % 100 ==0: print(‘epoch: %3d, step:%4d, kl_div: %5f, rec_loss:%9f‘ %(epoch, step, float(kl_div), float(rec_loss))) # evaluation 1: 从正太分布直接sample; z = tf.random.normal((batchsz, z_dim)) # 从正太分布中sample这个尺寸的 logits = model.decoder(z) # 通过这个得到decoder x_hat = tf.sigmoid(logits) x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() * 255. logits = x_hat.astype(np.uint8) # 标准的图片格式; save_images(x_hat, ‘vae_images/sampled_epoch%d.png‘ %epoch) # 直接sample出的正太分布; # evaluation 2: 正常的传播过程; x = next(iter(test_db)) x = tf.reshape(x, [-1, 784]) x_hat_logits, _, _ = model(x) # 前向传播返回的还有mu, log_var x_hat = tf.sigmoid(x_hat_logits) x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() * 255. x_hat = x_hat.astype(np.uint8) # 标准的图片格式; # print(x_hat.shape) save_images(x_hat, ‘vae_images/rec_epoch%d.png‘ %epoch)
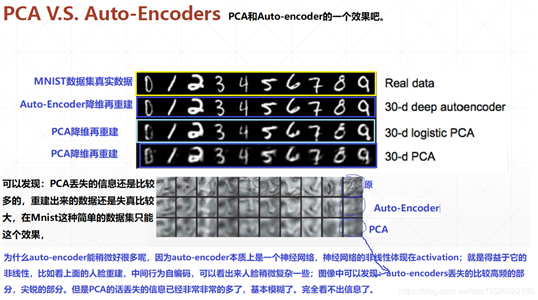
注意: 我们发现重建的图片相对原始图片存在模糊的现象,棱角美誉原图像那么锐利。这是因为 auto-encoder 求出来的 loss 是根据 distance (它会追求你的整体的 loss 变的更小,所以会存在模糊掉,所以图片的保真度不是特别好,这其实也是 GAN 存在的现象!)
1、AE.py
import os os.environ[‘TF_CPP_MIN_LOG_LEVEL‘]=‘2‘ import tensorflow as tf import numpy as np from tensorflow import keras from tensorflow.keras import Sequential, layers from PIL import Image from matplotlib import pyplot as plt tf.random.set_seed(22) np.random.seed(22) assert tf.__version__.startswith(‘2.‘) def save_images(imgs, name): new_im = Image.new(‘L‘, (280, 280)) index = 0 for i in range(0, 280, 28): for j in range(0, 280, 28): im = imgs[index] im = Image.fromarray(im, mode=‘L‘) new_im.paste(im, (i, j)) index += 1 new_im.save(name) h_dim = 20 batchsz = 512 lr = 1e-3 (x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data() x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255. # we do not need label train_db = tf.data.Dataset.from_tensor_slices(x_train) train_db = train_db.shuffle(batchsz * 5).batch(batchsz) test_db = tf.data.Dataset.from_tensor_slices(x_test) test_db = test_db.batch(batchsz) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) class AE(keras.Model): def __init__(self): super(AE, self).__init__() # Encoders self.encoder = Sequential([ layers.Dense(256, activation=tf.nn.relu), layers.Dense(128, activation=tf.nn.relu), layers.Dense(h_dim) ]) # Decoders self.decoder = Sequential([ layers.Dense(128, activation=tf.nn.relu), layers.Dense(256, activation=tf.nn.relu), layers.Dense(784) ]) def call(self, inputs, training=None): # [b, 784] => [b, 10] h = self.encoder(inputs) # [b, 10] => [b, 784] x_hat = self.decoder(h) return x_hat model = AE() model.build(input_shape=(None, 784)) model.summary() optimizer = tf.optimizers.Adam(lr=lr) for epoch in range(100): for step, x in enumerate(train_db): #[b, 28, 28] => [b, 784] x = tf.reshape(x, [-1, 784]) with tf.GradientTape() as tape: x_rec_logits = model(x) rec_loss = tf.losses.binary_crossentropy(x, x_rec_logits, from_logits=True) rec_loss = tf.reduce_mean(rec_loss) grads = tape.gradient(rec_loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) if step % 100 ==0: print(epoch, step, float(rec_loss)) # evaluation x = next(iter(test_db)) logits = model(tf.reshape(x, [-1, 784])) x_hat = tf.sigmoid(logits) # [b, 784] => [b, 28, 28] x_hat = tf.reshape(x_hat, [-1, 28, 28]) # [b, 28, 28] => [2b, 28, 28] x_concat = tf.concat([x, x_hat], axis=0) x_concat = x_hat x_concat = x_concat.numpy() * 255. x_concat = x_concat.astype(np.uint8) save_images(x_concat, ‘ae_images/rec_epoch_%d.png‘%epoch)
2、VAE.py
import os os.environ[‘TF_CPP_MIN_LOG_LEVEL‘]=‘2‘ import tensorflow as tf import numpy as np from tensorflow import keras from tensorflow.keras import Sequential, layers from PIL import Image from matplotlib import pyplot as plt tf.random.set_seed(22) np.random.seed(22) assert tf.__version__.startswith(‘2.‘) def save_images(imgs, name): new_im = Image.new(‘L‘, (280, 280)) index = 0 for i in range(0, 280, 28): for j in range(0, 280, 28): im = imgs[index] im = Image.fromarray(im, mode=‘L‘) new_im.paste(im, (i, j)) index += 1 new_im.save(name) h_dim = 20 batchsz = 512 lr = 1e-3 (x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data() x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255. # we do not need label train_db = tf.data.Dataset.from_tensor_slices(x_train) train_db = train_db.shuffle(batchsz * 5).batch(batchsz) test_db = tf.data.Dataset.from_tensor_slices(x_test) test_db = test_db.batch(batchsz) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape) z_dim = 10 class VAE(keras.Model): def __init__(self): super(VAE, self).__init__() # Encoder self.fc1 = layers.Dense(128) self.fc2 = layers.Dense(z_dim) # get mean prediction self.fc3 = layers.Dense(z_dim) # Decoder self.fc4 = layers.Dense(128) self.fc5 = layers.Dense(784) def encoder(self, x): h = tf.nn.relu(self.fc1(x)) # get mean mu = self.fc2(h) # get variance log_var = self.fc3(h) return mu, log_var def decoder(self, z): out = tf.nn.relu(self.fc4(z)) out = self.fc5(out) return out def reparameterize(self, mu, log_var): eps = tf.random.normal(log_var.shape) std = tf.exp(log_var)**0.5 z = mu + std * eps return z def call(self, inputs, training=None): # [b, 784] => [b, z_dim], [b, z_dim] mu, log_var = self.encoder(inputs) # reparameterization trick z = self.reparameterize(mu, log_var) x_hat = self.decoder(z) return x_hat, mu, log_var model = VAE() model.build(input_shape=(4, 784)) optimizer = tf.optimizers.Adam(lr) for epoch in range(1000): for step, x in enumerate(train_db): x = tf.reshape(x, [-1, 784]) with tf.GradientTape() as tape: x_rec_logits, mu, log_var = model(x) rec_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=x_rec_logits) rec_loss = tf.reduce_sum(rec_loss) / x.shape[0] # compute kl divergence (mu, var) ~ N (0, 1) # https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians kl_div = -0.5 * (log_var + 1 - mu**2 - tf.exp(log_var)) kl_div = tf.reduce_sum(kl_div) / x.shape[0] loss = rec_loss + 1. * kl_div grads = tape.gradient(loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) if step % 100 == 0: print(epoch, step, ‘kl div:‘, float(kl_div), ‘rec loss:‘, float(rec_loss)) # evaluation z = tf.random.normal((batchsz, z_dim)) logits = model.decoder(z) x_hat = tf.sigmoid(logits) x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255. x_hat = x_hat.astype(np.uint8) save_images(x_hat, ‘vae_images/sampled_epoch%d.png‘%epoch) x = next(iter(test_db)) x = tf.reshape(x, [-1, 784]) x_hat_logits, _, _ = model(x) x_hat = tf.sigmoid(x_hat_logits) x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255. x_hat = x_hat.astype(np.uint8) save_images(x_hat, ‘vae_images/rec_epoch%d.png‘%epoch)
转自:https://zhangkaifang.blog.csdn.net/article/details/90297041
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution)。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
在TF中会大量使用到正态分布,熟练的使用它,也是使用TF的基本功之一。下面来看一下在Python中如何使用。
用numpy来获取一个标准正态分布的样例
num = 100000
mu = 0
sigma = 1
s = np.random.normal(mu, sigma, num)
一维正太分布如上面定义所说,正如一个“钟形”

或者如下两者
s = sigma * np.random.randn(num) + mu
和
s = sigma * np.random.standard_normal(num) + mu
效果都如之前的图片
mu控制函数中心位置左右移动,如下mu=6的场景

sigma=10的场景

可见,mu为正数,函数曲线向右移动,反之,向左移动;sigma越大,分布越宽;sigma越小分布越窄。
记住这个特性,在获取一维正太分布数据时很有帮助。
二维正太分布的公式如下,
二维正太分布使用不一样的numpy函数,multivariate_normal
num = 40000
mean = np.array([0,0])
cov = np.eye(2)
ms = np.random.multivariate_normal(mean, cov, num)
二维标准正太分布如下,不在是一个“钟”,而像一个“圆”

这里的参数也有变化。
mean表示二维数组每一维的均值;是一个(1,2)矩阵。
cov表示二维数组的协方差;是一个(2,2)矩阵。
可以看出来mean是圆的圆点,那么是不是改变了mean,圆就会发生移动呢? 我们试一下。
num = 40000
mean = np.array([4,8])
cov = np.eye(2)
ms = np.random.multivariate_normal(mean, cov, num)

那么cov协方差代表的意义也通过实验来看一下,
num = 40000
mean = np.array([0,0])
cov = np.array([[5,0],[0,1]])
ms = np.random.multivariate_normal(mean, cov, num)

原文:https://www.cnblogs.com/zhangxianrong/p/14731729.html