动态规划——72. 编辑距离

题目：

思路：

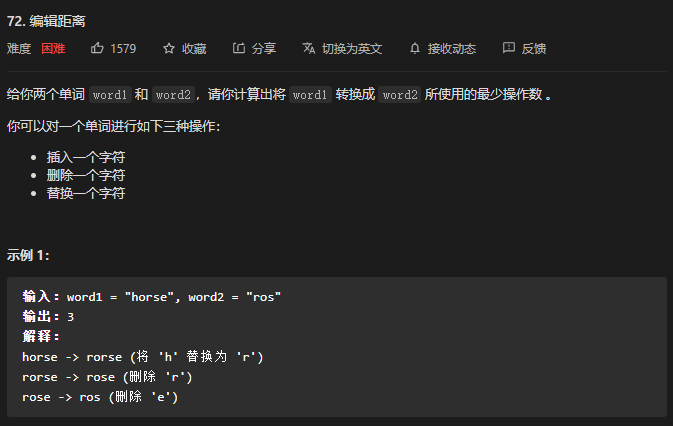
1. dp数组的定义：dp[i] [j]代表word1[0, ... , i], word2[0, ... , j]的最小编辑距离。

2. base_case：就是分别考虑i=0的情况

   for(int i = 0; i <= m; i++){dp[i][0] = i;}
   
   for(int i = 0; i <= n; i++){dp[0][i] = i;}
   

3. 状态转移方程：若是相等则不用操作，继续往下看。

   不相等的话，得考虑三个操作：

   ? 插入：前移 j，继续跟 i 对比，相当于直接在 s1[i] 插入一个和 s2[j] 一样的字符。

   ? 删除：前移i，继续跟j对比，相当于直接把 s[i] 这个字符删掉。

   ? 替换：同时前移 i，j 继续对比，相当于直接把 s1[i] 替换成 s2[j]，这样它俩就匹配了。

代码：

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        int dp[m+1][n+1];
        for(int i = 0; i <= m; i++){
            dp[i][0] = i;
        }
        for(int i = 0; i <= n; i++){
            dp[0][i] = i;
        }
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
                else dp[i][j] = min(min(dp[i-1][j], dp[i-1][j-1]), dp[i][j-1]) + 1;
            }
        }
        return dp[m][n];
    }
};

Rank：

Tips：

动态规划——72. 编辑距离

原文：https://www.cnblogs.com/lzyrookie/p/14731360.html