一直对张量抱有执念,当初张量分析晕晕忽忽,现在也都忘光光了,啥时候仔细学学吧,到时候顺便把这里再捋捋
材料力学中,平面一点的应力状态可以用应力张量表示
按我个人理解,标量 a 可以表示一个量的大小;向量 \((a,b)^T\) 可以表示一个量的大小和方向, a 和 b 为对应基向量方向上的大小;一个二阶张量(本质:多重方向性的量)同样可以表示一个量的大小和方向,该方向由两个矢量表示(应力:作用面和作用方向),\(\sigma_{xx}\) 为对应基向量上的大小(垂直于x轴的面,平行于x轴方向)。
在给出的平面应力二阶张量中,作用面方向可通过 2 个基向量表示,作用方向也可以通过 2 个基向量表示,通过组合可以得到 4 组基
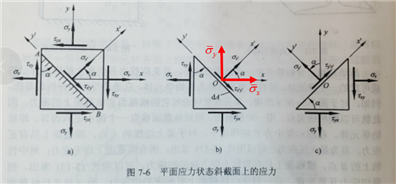
现在指定一个单位方向 \(\vec{n}\),\(\vec{n}\) 确定的平面上的应力状态可表示为
上式的应力矩阵为转置状态,!!!这是从力的平衡条件推导得出的!!!
细化分析
从力的平衡条件很容易可以推导出上式,我为了仔细理解,现从向量点积的角度考虑 \(\overline\sigma_x\) 的计算:
前面提到,二阶张量具有多重方向性,一个量的方向需要两个矢量描述。在平面应力问题中, \([\sigma_{xx}]\) 表示作用在垂直于x轴的面,并平行于x轴方向上的应力大小。
这里作用面可通过单位法向量描述,作用方向可通过单位矢量描述,其中一个单位矢量可由两个基向量形成。也即作用面可通过两个基向量表示,作用方向也可通过两个基向量表示,作用面基向量 (我称作 -- 基面) 和作用方向基向量 (我称作 -- 基向) 两两组合形成的二阶张量 [基向量???] 就可以用来同时表示作用面和作用方向。
从数学的向量积来看,一个向量与单位向量的点积等于该向量在单位向量方向上的投影长度(分量大小)
观察 \([\sigma_{xx} \ \tau_{yx}]\) 可知,这两个应力的作用面分别在不平行的两个面上(可以选做基面),但作用方向均为 x 方向,因此我们可以基于 \([\sigma_{xx} \ \tau_{yx}]\) 提取出任意平面上作用在 x 方向上的应力的一组基,而 \([\sigma_{xx} \ \tau_{yx}]\) 是每个基对应的大小,也即我们考虑的一点应力状态在这组基下的大小 (我先把 \([\sigma_{xx} \ \tau_{yx}]\) 理解为一个 “向量”,尽管ta并不是)。
从向量积的角度考虑,我们考虑的一点应力状态在这组基下的 “向量” 与任意面单位法向量的点积就等于:该 “向量” 在任意面上的分量大小。又由于该 ”向量“ 始终表示作用的 x 方向,因此点积结果表示为:在作用方向为 x 的方向上,该 “向量” 在任意面上的分量大小
\(\overline\sigma_y\) 的计算同理。
这里面还有许多数学概念并不清晰,只是我的强行解释,但我又希望能够对应力的坐标变换进行数学解释,因而写了些许拙见
因为应力矩阵是对称矩阵,所以材料力学书中大都写为一个无法理解的形式
同样无法理解的是,书中还将应力的坐标转换写成
其中 \([\lambda]\) 为坐标转换矩阵,并且 \([\lambda]^T = [\lambda]^{-1}\) ,书中为求简便将这一定义忽略,不利于理解,正确的定义应该是
这也是相似矩阵的定义,因此 $\left[ \begin{matrix} \sigma_{ij}^{‘} \end{matrix} \right] $ 与 $\left[ \begin{matrix} \sigma_{ij} \end{matrix} \right] $ 在不同坐标系下表示同一个物理量。
主应力,主应力方向,应力不变量,应力偏张量
待续...

最后更新于 2021年5月5日 --- 最初发表于 2021年5月5日
原创作者:LitBro
关于作者:咕咕咕
本文链接: [ https://www.cnblogs.com/LitBro/p/14731462.html]
版权声明:本文采用 BY-NC-SA协议,转载或引用请注明出处!
关于后续:碍于学业不精,如有描述不当,还请见谅并非常感谢指出
原文:https://www.cnblogs.com/LitBro/p/14731462.html