支持向量机-SVM推导(C语言源码)

很久之前就想把SVM系统的解析一下，争取把西瓜书的这一部分顺一遍，并用C语言对各个部分进行解析，加深理解。

基本概念

给定训练样本集\(D = {(Xl,Yl) ， (X2，Y2) , . . . , (Xm, Ym)}\), \(Yi ε{-1, 1)\)，分类学习最基本的想法就是基于训练、集D 在样本空间中找到一个划分超平面、将不同类别的样本分开。

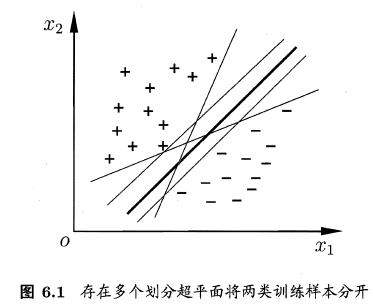
在样本空间中，划分超平面可通过如下线性方程来描述:

其中，\(w = (w1;w2，... ， ωd)\)?决定了超平面的方向; b 为位移项，决定了超平面与原点之间的距离.显然，划分超平面可被法向量ω 和位移b 确定，下面我们将其记为(矶的.样本主R 间中任意点2 到超平面(矶的的距离可写为:

间隔与支持向量

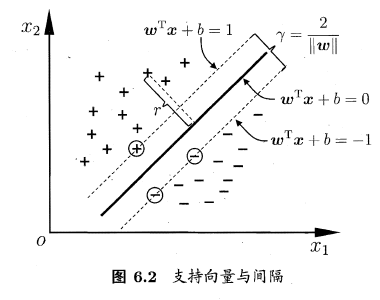
间隔：，两个异类支持向量到超平面的距离之和，即\(\gamma = \frac{2}{\omega}\)
支持向量：距离超平面最近的这几个训练样本点使式(6.3) 的等号成立，

SVM的基本型

对偶问题

那么?如何求解式(6.11) 呢?不难发现j 这是一个三次规划问题?可使用通
用的二次规划算法来求解;然而?该问题的规模正比于训练样本数7 这会在实际
任务中造成很大的开销.为了避开这个障碍，人们通过利用问题本身的特性，提
出了很多高效算法， SMO (Sequential Minimal Optimization) 是其中一个著名
的代表[Platt ， 1998].

SMO算法

SMO的基本思路是先固定向之外的所有参数，然后求向上的极值.由于存在约束艺汇1 叫ντ 工0 ，若固定向之外的其他变量?则αz 可由其他变量导出.于是， SMO 每次选择两个变量问和町，并固定其他参数.这样，在参数初始化
后， SMO 不断执行如下两个步骤直至收敛:

1. 选取一对需更新的变量\(\alpha_i\)和\(α_j\);
2. 固定\(α_i\)和\(α_j\)以外的参数，求解式(6.11)获得更新后的叫\(α_i\)和\(α_j\).

注意到只需选取的问丰IJα3 中有一个不满足KKT 条件(6.13) ，目标函数就会在选代后减小[Osuna et al., 1997]. 直观来看， KKT 条件违背的程度越大?则变量更新后可能导致的目标函数值减幅越大.于是， SMO 先选取违背KKT 条件程度最大的变量.第二个变量应选择一个使目标函数值减小最快的变量，但由于比较各变量所对应的目标函数值减幅的复杂度过高，因此SMO 采用了一个启发式:使选取的两变量所对应样本之间的问隔最大. 种直观的解释是，这样的两个变量有很大的差别，与对两个相似的变量进行更新相比，对它们进行更新会带给目标函数值更大的变化.

核函数

对于线性不可分的训练样本，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分.

核函数定理

常用的核函数

支持向量机-SVM推导(C语言源码)

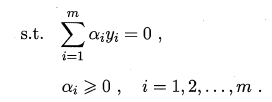
原文：https://www.cnblogs.com/guoben/p/14738321.html