斐波那契查找

• 补充知识点

黄金分割：黄金分割点是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽，因此称为黄金分割。

斐波那契：斐波那契数列又称黄金分割数列：1、1、2、3、5、8、13、21、····，数列的第一个数为1，第二个数为1，随后的每一个数为前两个相邻数之和，F(k)=F(k-1)+F(k-2); 两个相邻数的比例无限接近于黄金分割值0.618。

• 条件

1. 要查找的数组必须是有序的

2. 使用斐波那契查找之前，源数组的长度必须扩充为一个斐波那契数

• 基本介绍

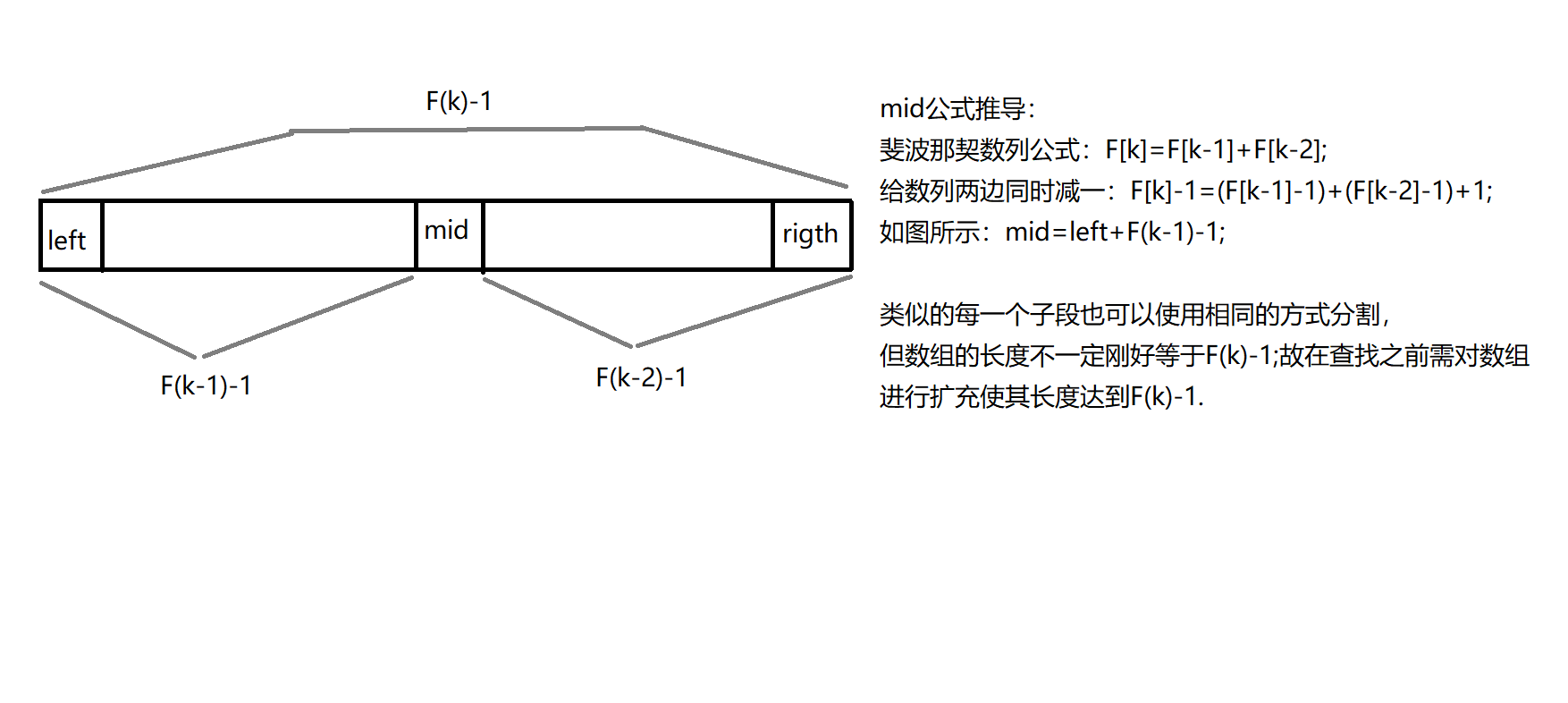
斐波那契查找原理与二分查找和插入查找法方法相似，仅仅改变了中间节点mid的位置，mid不再是中间或者插值得到的，而是位于黄金分割点附近mid=right+F(k-1)-1（F为斐波那契数列，k为斐波那契数列的第几个数）

• 实现步骤

实现方法前两种方法相似，仅仅改变中间值（mid）的查找方式mid=right+F(k-1)-1;

1. 创建一个方法fib()用来获取存储的斐波那契数的数组。

2. 创建一个临时数组temp,目的：扩充源数组的长度为一个斐波那契数。

3. 扩充源数组的长度为斐波那契数，扩充部分的值填充为源数组的最后一个值

4. 循环比较temp[mid]与要查找的数num的值是否相等

   ? （1）若temp[mid]>num 向mid的左边

• 求mid图解

• 代码实现

//斐波那契查找
public class FibSearch {
    public static void main(String[] args) {
        //System.out.println(Arrays.toString(fib()));
        int[] arr={0,3,5,7,8,12,25,48,48,56,98,99};
        int num=fibSearch(arr,3);
        System.out.println(num);
    }
    public static int max=20;//斐波那契数组的最大容量
    //获取存储前max个斐波那契数的数组
    public static int[] fib(){
        int[] arr=new int[max];
        arr[0]=1;
        arr[1]=1;
        for(int i=2;i<arr.length;i++){
            arr[i]=arr[i-1]+arr[i-2];
        }
        return arr;
    }

    //斐波那契查找算法
    // mid=low+F(k-1)-1;
    public static int fibSearch(int[] arr,int key){
        int left=0;
        int right=arr.length-1;
        int k=0;//对应取斐波那契数列的下标
        int[] F=fib();//创建一个容量为20的斐波那契数组
        //原数组的长度不一定刚好等于F(k)-1,故使F[k]-1大于或等于数组长度；之后使用数组拷贝将源数组扩充，
        while(arr.length>F[k]-1){
            k++;
        }
        //数组拷贝使之长度为F[k]-1
        int[] temp=Arrays.copyOf(arr,F[k]);//此处为什么不是F[k-1]原因：数组拷贝范围前闭后开
        //将数组扩充部分的值填充为源数组中的最后一个值
        Arrays.fill(temp,arr.length,temp.length,arr[arr.length-1]);
        while(left<=right){
            int mid=left+F[k-1]-1;
            if(temp[mid]>key){
                right=mid-1;
                k--;//此时k变化的原因为：f(k)=f(k-1)+f(k-2);向左递归，根据公式，参数值-2
            }else if(temp[mid]<key){
                left=mid+1;
                k-=2;//此时k变化的原因为：f(k)=f(k-1)+f(k-2);向右递归，根据公式，参数值-1
            }else {
                //若查找的值为原数组的最后一个值，由于数组扩充后扩充部分填充的的是源数组最后一个值，故所查找的mid有可能越界
                if(mid<arr.length){
                    return mid;
                }else {//此时mid已经越界，返回原数组长度的最后一个位置
                    return arr.length-1;
                }
            }
        }
        return -1;
    }
}

斐波那契查找

原文：https://www.cnblogs.com/ekig/p/14747408.html