#include<bits/stdc++.h>
using namespace std;
int main()
{
int a,b,c,d;
cin>>a>>b>>c>>d;
cout<<min(min(a,b),min(c,d));
return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int M=1010;
int a[M],b[M];
int main()
{
int n,m,t;
cin>>n>>m>>t;
for(int i=0;i<m;i++) cin>>a[i]>>b[i];
bool flag=true;
int cur=n,pre=0;
for(int i=0;i<m;i++){
int gap=a[i]-pre;
cur-=gap;
if(cur<=0){
flag=false;
break;
}
int add=b[i]-a[i];
cur=(cur+add>=n?n:cur+add);
pre=b[i];
}
cur-=t-pre;
if(cur<=0){
flag=false;
}
if(flag) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
??给定一个长度为\(L\)的铁棒，我们需要将其切成\(12\)段，并保证每一段的长度为整数。现需要我们找出所有的切割方法。如果两个切割方案有一个位置不同，则视为不同方案，题目保证结果大小不会超出\(2^{63}\)。
??对于给定长度为\(L\)的铁棒，要把它分割成\(12\)段，相当于从内部的\(L-1\)个点中挑选出\(11\)个不同的点进行切割。那么实际上结果就是我们的\(C_{L-1}^{11}\)。
??这里需要注意的是如果我们直接按照组合数的计算公式去计算，会存在溢出，因此我们需要对计算公式进行转化。
由于分子的个数与分母的个数是完全相同的，因此我们可以边算边除，即
也就是
从中我们可以看出
因此我们就只需要按照这个公式求解结果即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
{
int n;
cin>>n;
LL pre=1;
LL cur=0;
for(int i=0; i<11; i++)
{
cur=pre*(n-(i+1))/(i+1);
pre=cur;
}
cout<<cur<<" "<<endl;
return 0;
}
??给定一行方块，方块颜色为白色或者蓝色，现要使用一个长度为\(k\)的邮票，遮挡住白色部分并且不能遮挡到蓝色方块，邮票间可以相互覆盖，要求求出覆盖所需的最少邮票数量。
??想要使用最少的数量覆盖尽可能大的区域，就需要使用尽可能长的邮票来覆盖，由于不能覆盖到蓝色方块，因此我们\(k\)的最大取值为夹在蓝色方块中的白色方块数量的最小值。由于可以重复覆盖，因此对于一个长度为\(w\)的白色方块，我们只需要使用\((w+k-1)/k\)个邮票就可以。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
vector<int> pos(m);
for(int i=0;i<m;i++)
cin>>pos[i];
pos.push_back(n+1);
vector<int> cnt;
sort(pos.begin(),pos.end());
int pre=0;
int mmin=(int)1e9;
for(int i=0;i<(int)pos.size();i++)
{
int gap=pos[i]-pre-1;
pre=pos[i];
if(!gap) continue;
mmin=min(mmin,gap);
cnt.push_back(gap);
}
long long ans=0;
for(int i=0;i<(int)cnt.size();i++)
ans+=(cnt[i]+mmin-1)/mmin;
cout<<ans;
return 0;
}
??给定两个长度分别为\(N\),\(M\)的数组\(A\)和\(B\)，通过移除\(A\)或者\(B\)中的元素，使得新的两个数组元素个数相同，现记\(x\)为两个数组移除元素的个数，\(y\)为两个新数组中相同位置不同元素的个数，求出\(x+y\)的最小值。
??容易想到的是搜索所有可能性，对于一个元素来说是保留还是直接删除，由于还有可能相同个数的情况下还需要删除元素才能得到最小值的情况，因此暴力求解的做法实现困难并且时间复杂度高。我们考虑使用动态规划的方式来计算。
??定义数组\(dp[i][j]:\)\(A\)的前\(i\)个元素与\(B\)的前\(j\)个元素的\(x+y\)的最小值。
??现在对状态集合进行划分(闫式dp分析)
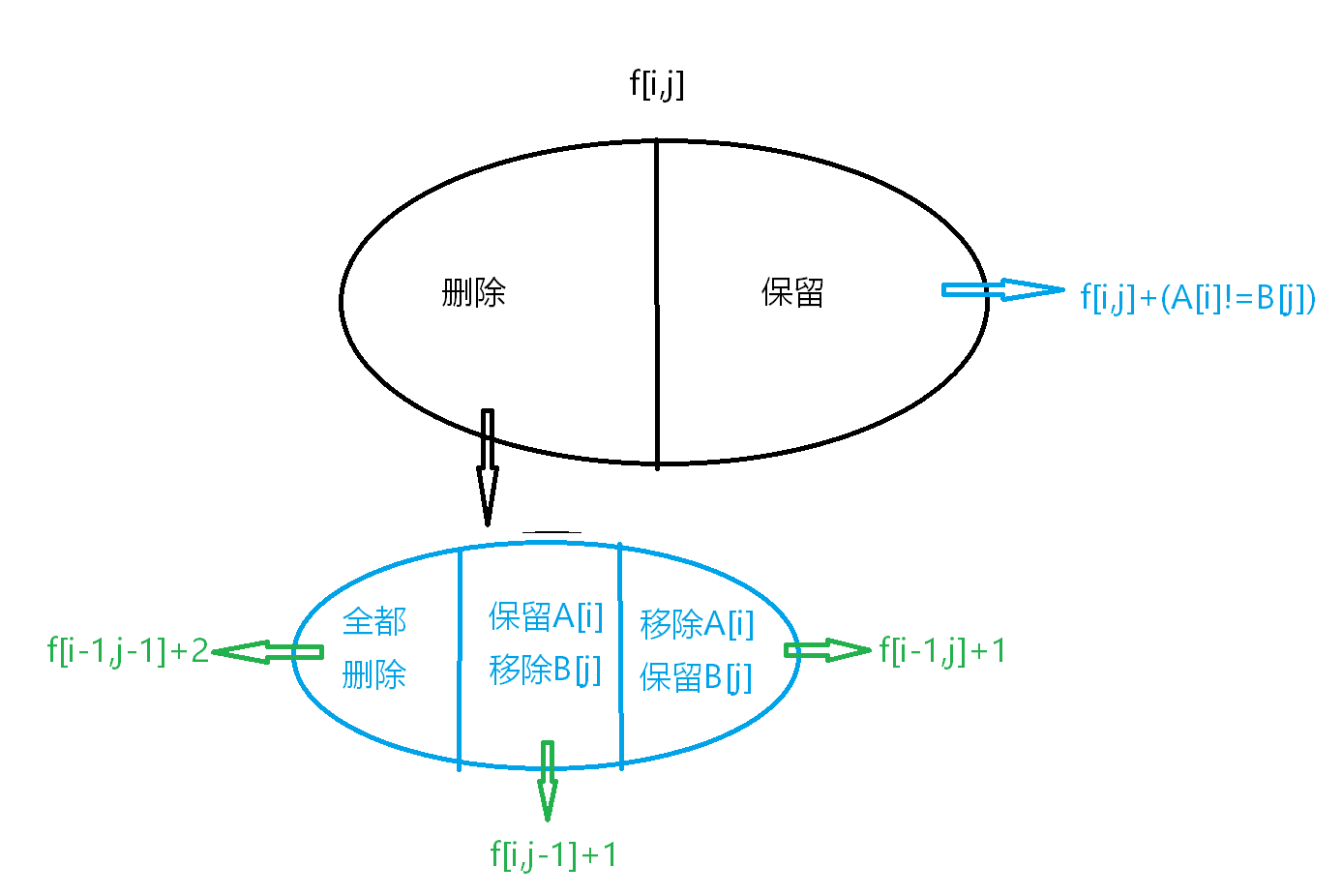（在删除集合中，全都删除的集合被另外两个集合覆盖，可以不用进入比较）
??还需要考虑到边界情况，\(f[i][j]=i+j(i=0 or j=0)\)
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N], b[N];
int dp[N][N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= m; i++)
cin >> b[i];
memset(dp,0x3f,sizeof dp);
for (int i = 0; i <= m; i++)
dp[0][i] = i;
for (int i = 0; i <= n; i++)
dp[i][0] = i;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1;
//dp[i][j]=min(dp[i][j],dp[i-1][j-1]+2);
dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + (a[i] != b[j]));
}
}
cout << dp[n][m];
return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int N=300010;
int n,q;
int a[N];
struct node
{
int l,r;
int sum;
}tr[N*4];
void pushup(int x)
{
tr[x].sum=tr[x<<1].sum^tr[x<<1|1].sum;
}
void build(int x,int l,int r)
{
tr[x]={l,r,a[l]};
if(l==r) return;
int mid=(l+r)>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
pushup(x);
}
void modify(int x,int l,int d)
{
if(tr[x].l==l&&tr[x].r==l)
{
tr[x].sum^=d;
return; //
}
int mid=(tr[x].l+tr[x].r)>>1;
if(l<=mid) modify(x<<1,l,d);
else modify(x<<1|1,l,d);
pushup(x);
}
int query(int x,int l,int r)
{
if(tr[x].l>=l&&tr[x].r<=r)
{
return tr[x].sum;
}
int mid=(tr[x].l+tr[x].r)>>1;
int ans=0;
if(l<=mid) ans^=query(x<<1,l,r);
if(r>mid) ans^=query(x<<1|1,l,r);
return ans;
}
int main()
{
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(q--)
{
int t,x,y;
cin>>t>>x>>y;
if(t==1)
{
modify(1,x,y);
}
else
{
cout<<query(1,x,y)<<endl;
}
}
return 0;
}
??考虑到\(sum(l,r)=sum(1,l-1) \oplus sum(1,r)\)，可以用前缀异或和来做，因此可以维护前缀异或和，操作一可以看到是数组数组中的单调加，因为异或操作符合交换律，因此可以使用树状数组来做。
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int n,q;
int bit[N];
int lowbit(int x)
{
return x&(-x);
}
int sum(int i)
{
int s=0;
while(i>0)
{
s^=bit[i];
i-=lowbit(i);
}
return s;
}
void add(int i,int x)
{
while(i<=n)
{
bit[i]^=x;
i+=lowbit(i);
}
}
int main()
{
cin>>n>>q;
for(int i=1;i<=n;i++){
int t;
cin>>t;
add(i,t);
}
while(q--)
{
int t,x,y;
cin>>t>>x>>y;
if(t==1) add(x,y);
else cout<<(sum(y)^sum(x-1))<<endl;
}
return 0;
}
AtCoder Beginner Contest 185题解
原文：https://www.cnblogs.com/Daneyx/p/14753098.html