做凸包和一些 USACO 的题要用

Start

1. 既有大小，又有方向的量，如速度

2. 表示方法：字母上加箭头 \(\overrightarrow{a}\)

3. 若向量起点为 \(A\) 终点为 \(B\) 向量可表示为 \(\overrightarrow{AB}\)

4. 向量的大小：表示为 \(|\overrightarrow{a}|\) 或 \(|\overrightarrow{AB}|\)

5. 零向量：\(\overrightarrow{O},|\overrightarrow{O}|=O\)，起点和终点重合，方向任意

6. 单位向量：长度为一个单位的向量

7. 在平面直角坐标系中，将向量 \(\overrightarrow{a}\) 平移，使起点和原点重合，终点位于点 \((x,y)\) ，

   则实数对 \((x,y)\) 为向量 \(\overrightarrow{a}\) 的坐标，记为 \(\overrightarrow{a}=(x,y)\) 。

8. 加法：\(\overrightarrow{A}+\overrightarrow{B}=(x_1+x_2,y_1+y_2)\)

9. 向量加法满足交换律和结合律

10. 减法 \(\overrightarrow{A}-\overrightarrow{B}=(x_1-x_2,y_1-y_2)\)

11. 

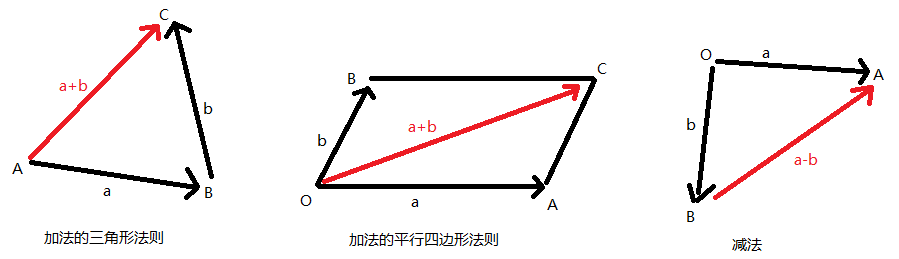
12. 已知 \(A(x_1,y_1),B(x_2,y_2)\)，则\(\overrightarrow{AB}=B-A\)

点积

1. 点积就是 \(a\cdot b=x_1x_2+y_1y_2\)

2. 几何意义：两个向量的夹角。

3. 点积有以下性质

• \(a\cdot b=0\)，则 \(a\perp b\)
• \(a\cdot b<0\)，则夹角 \(>90^\circ\)
• \(a\cdot b>0\)，则夹角 \(<90^\circ\)
• 自乘，\(|a|^2=a\cdot a\)
• 交换律和结合律

叉积

1. 叉积就是 \(a\times b=\det \left [ \begin{array}{} x_1 & x_2 \\ y_1 & y_2 \end{array}\right ]=x_1y_2-x_2y_1\)

2. 几何意义：两个向量的起点共点时，所形成的平行四边形面积

3. 性质

• \(a\times b=0\)，a 和 b 共线，方向相同或相反

• \(a\times b>0\)，a 在 b 顺时针方向

• \(a\times b<0\)，a 在 b 逆时针方向

向量初步

原文：https://www.cnblogs.com/KonjakLAF/p/14760825.html