Task02：基于统计学的方法（3天）

学习基于统计学的异常检测方法

统计学方法的优缺点

• 优点：
  • 如果统计假定成立，这种方法会非常有效
  • 统计方法的置信区间可以作为额外的信息帮助决策
• 缺点：
  • 这类方法严重依赖数据集的分布假定

掌握基于高斯分布的方法和HBOS算法

基于高斯分布的方法

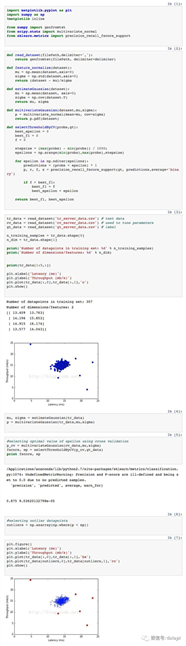
一元检测的代码

import numpy as np 
import seaborn as sns 
import matplotlib.pyplot as plt 
# 随机生成的数据
data = np.random.randn(50000)*50  + 20 
sns.boxplot(data=data)

HBOS算法

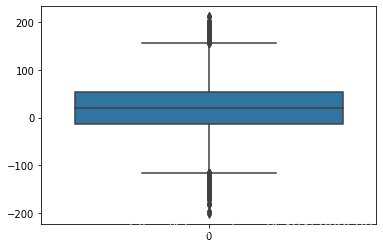
简单来说就是降维，先求每个维度的概率，再合并，降到一维，最终目的是求样本的概率密度

1. 为每个数据维度做出数据直方图。对分类数据统计每个值的频数并计算相对频率。对数值数据根据分布的不同采用以下两种方法：
   • 静态宽度直方图：
     标准的直方图构建方法，在值范围内使用k个等宽箱。样本落入每个桶的频率（相对数量）作为密度（箱子高度）的估计。
     时间复杂度：O (n)
   • 动态宽度直方图：
     首先对所有值进行排序，然后固定数量的个连续值装进一个箱里，其中N是总实例数，k是箱个数；直方图中的箱面积表示实例数。因为箱的宽度是由箱中第一个值和最后一个值决定的，所有箱的面积都一样，因此每一个箱的高度都是可计算的。这意味着跨度大的箱的高度低，即密度小，只有一种情况例外，超过k个数相等，此时允许在同一个箱里超过
2. 对每个维度都计算了一个独立的直方图，其中每个箱子的高度表示密度的估计。然后为了使得最大高度为1（确保了每个特征与异常值得分的权重相等），对直方图进行归一化处理。
   最后，每一个实例的HBOS值由根据公式计算。

运行示例

利用generate_data函数生成异常值占比为10%的toy set

from pyod.utils.data import generate_data,evaluate_print
contamination = 0.1  # percentage of outliers
n_train = 200  # number of training points
n_test = 100  # number of testing points

X_train, y_train, X_test, y_test = generate_data(
   n_train=n_train, n_test=n_test, contamination=contamination)

导入hbos，生成一个HBOS的异常检测器对象。 用fit()方法拟合数据

from pyod.models import hbos
from pyod.utils.example import visualize 

clf = hbos.HBOS()
clf.fit(X_train)
y_train_pred = clf.labels_
y_train_socres = clf.decision_scores_
y_test_pred = clf.predict(X_test)  # 返回未知数据上的分类标签 (0: 正常值, 1: 异常值)
y_test_scores = clf.decision_function(X_test)  #  返回未知数据上的异常值 (分值越大越异常)

获得结果并进行可视化观察

clf_name = ‘HBOS‘
print("\nOn Test Data:")
evaluate_print(clf_name, y_test, y_test_scores)
visualize(clf_name, X_train, y_train, X_test, y_test, y_train_pred,
   y_test_pred, show_figure=True, save_figure=False)

(2) 理解非参数的方法

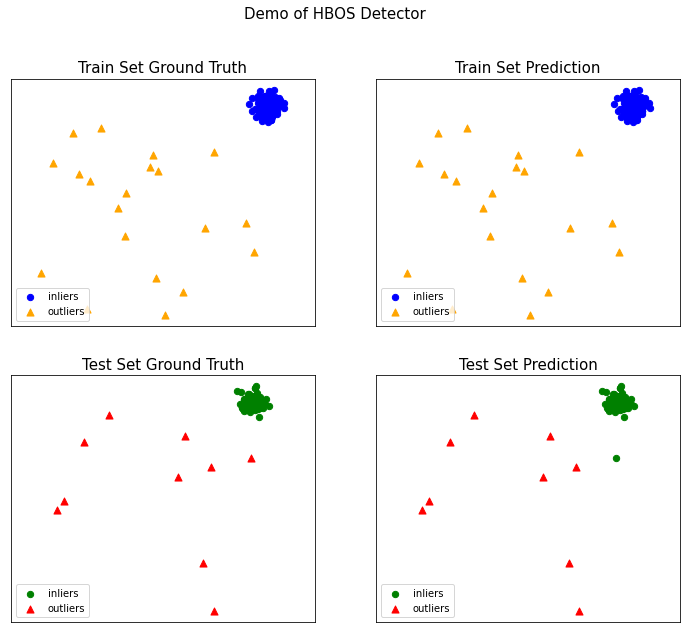
在异常检测的非参数方法中，正常数据的模型从输入数据进行学习，而非假定一个先验，非参数方法通常对数据做较少的假定，因此在很多场景下可以使用,如采用直方图进行异常检测：

• 构造直方图：使用输入数据构造一元或者多元直方图
• 检测异常点：
  • 若一个对象落入直方图的某些箱中，则认为数据是正常的，否则认为是异常的
  • 更复杂的方法是采用直方图为每个对象赋予一个异常点得分，如令对象的异常点得分为该对象落入的箱的容积的倒数

采用直方图的方法是一种非参数方法(不需要对数据的分布进行假定)，但是缺点在于需要指定直方图的相关参数(如箱子是等宽还是等深的，直方图中每个箱子的大小等)，如果箱子太小，则许多正常对象会被误认为异常点，而箱子太大时许多异常点会被认为是正常的。

Task02：基于统计学的方法（3天）

原文：https://www.cnblogs.com/Vincy-BLOG/p/14768058.html