1 一维与二维离散傅里叶变换
以周期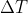 
对函数 f(t) 采样可表示为 
，
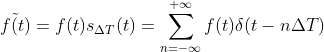对采样函数进行傅里叶变换得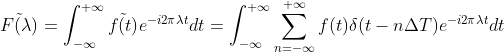 
，
整理得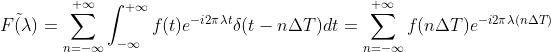 
。
由于对函数 f(t) 的采样周期为 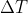，采样函数的傅里叶变换的一个完整周期为 
，
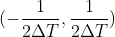同样的，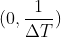
也是采样函数的傅里叶变换的一个完整周期，只是这个周期不是以原点对称的。
在 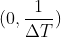区间中取 M 个点，则第 m 个点的频率为 
，
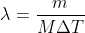带入公式得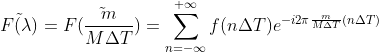 
，
其中，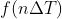
为连续函数 f(t) 对应的 M 个离散值，
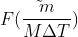为取样函数 
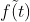的傅里叶变换对应的 M 个离散值，
整理公式得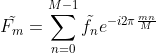 
（由于函数仅在 [0,M-1] 上有非零值，故真实求和区间为 [0,M-1]）。
因此，一维离散傅里叶变换对为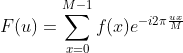 
，
。
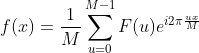类似的，二维离散傅里叶变换对为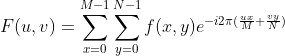 
，
。
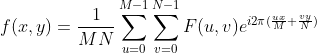2 傅里叶变换的性质
1）傅里叶变换平移特性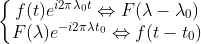 
，
用指数项乘以 f(t) 使得傅里叶变换后原点移动到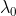 
处，
使用负指数乘以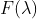 
使得反傅里叶变换后原点移动到 
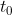处，证明如下：
，
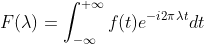使用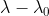 
替换 
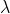得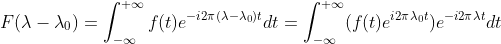 
，
因此有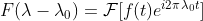 
，类似推导可得 
。
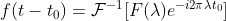将平移特性扩展到二维离散变量上有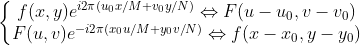 
。
2）离散傅里叶变换一定具有周期特性，因为离散傅里叶变换的频率取值在 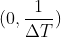区间内，有限频率导致必然具有周期性，
连续傅里叶变换频率取值为无穷大，所以连续傅里叶变换一般不具有周期性（但也有所有频率都一样的函数）。
离散傅里叶变换周期性可表示为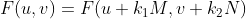 
。
观察公式 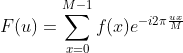或 ，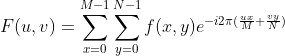
发现频率取值在 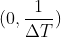之间，而一个完整的频率应该在 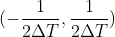之间，如下图：
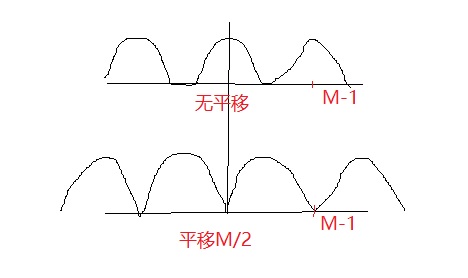
如果直接应用公式进行傅里叶变换，得到的频率为 [0,M-1]区间，这是两个半周期组成的一个周期。
在图像中则表现为低频信号分布在4个角落，这显然不便于观察频率信息。
结合傅里叶变换的平移特性，可以将原函数乘以一个正指数项，使得平移后傅里叶变换再 [0,M-1]区间正好是一个完整的周期。
将原函数平移 M/2 可以实现该目标，具体分析如下：
原函数平移 M/2 得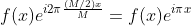 
，
由于 x 为非负整数，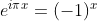
,
最终得到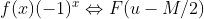 
。
对于二维离散变量有相似结论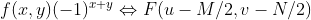 
。
未完。。。
原文：https://www.cnblogs.com/luofeiju/p/14767403.html