前言

本文主要介绍插入排序和能略微提升其性能的代码细节，以及插入排序的改进——希尔排序

一、插入排序

先上代码：

//原始插入排序
void originInsertSort(vector<int> iv) {
	for (size_t i = 1; i < iv.size(); ++i) {
		//不断交换直至 a[i]>=a[i-1]
		for (size_t j = i; i != 0 && iv[j] < iv[j - 1]; --j) {
			swap(iv[j], iv[j - 1]);
		}
	}
}

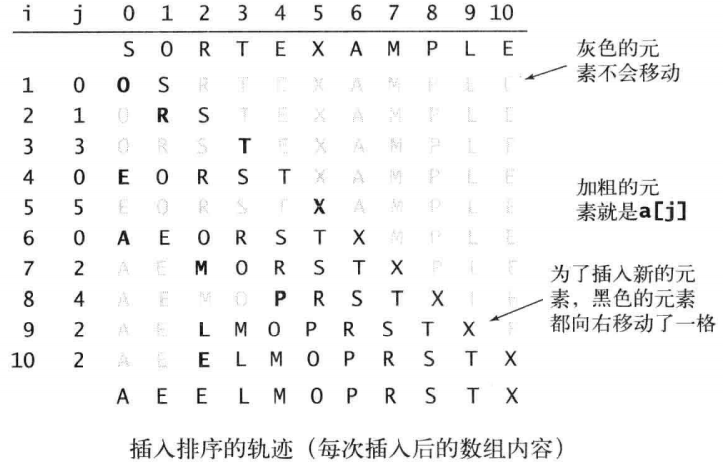
插入排序是通过将 0 到 n-1 中每一个 i ，将 a[i] 与 a[0] 至 a[i-1] 中比它小的数依次交换。排序从左往右进行，因此 i 左边的元素都是有序的，当 i 到末尾时，整个数组就都是有序的了。

插入排序的时间复杂度和数组元素一开始的顺序有关，最好情况下 (元素已排好序)，只需要 n-1 次比较和0次交换即可完成 (O(N)级)。而在最坏情况下(元素完全逆序)，需要Σ (n-1）次比较和相同次数的交换 (O(N2)级)。

二、细节改进

在原始的插入排序代码中，内循环为了防止循环到最后时的数组溢出，每次都需要判断 i 是否不为0，(平均需要判断n2/4次)。而在交换时，需要两次从数组中取数。这些无疑增加了不必要的时间开销。对此我们可以进行一些细节改进：先用选择排序将第一位的数排好作为哨兵 (用选择排序只找出第一位只需要n-1次判断和1次交换)，来去除内循环的判0。将交换操作改为右移操作，以在每次交换时减半访问数组的次数。

这些细节虽然不能让算法在整体的时间复杂度上有所改进，但是实际运行时可以真正地减少时间开销。

上代码：

//哨兵不交换插入排序
void insertSort(vector<int>& intVe) {
	if (intVe.size() == 0) { return; }
	unsigned tempMin = 0;
	for (size_t i = 1; i < intVe.size(); ++i) {
		if (intVe[tempMin] > intVe[i]) {
			tempMin = i;
		}
	}
	swap(intVe[0], intVe[tempMin]);
	for (size_t i = 2; i < intVe.size(); ++i) {
		size_t j = i;
		int temp = intVe[j];
		for (; intVe[j - 1] > intVe[j]; --j) {
			intVe[j] = intVe[j - 1];
		}
		intVe[j] = temp;
	}
}

经数据实验，对于10万个随机double，原始插入排序所需时间是改进后所需时间的1.1倍。

三、希尔排序

相比一个一个比较并交换的插入排序，希尔排序对其进行了改进。交换不相邻的元素对数组局部进行排序，在最后用插入排序将局部有序的数组进行排序。

希尔排序的思想是使数组中任何间隔为h的元素都是有序的。在进行排序时，如果h很大，我们就可以将元素移动的相对于原位置很远的地方，为接下来的小一点的h排序创造方便。在最后，h缩小为1时，所需排序的数组和原来相比已经有序多了，这时进行插入排序（h为1的希尔排序）所需时间会大大降低。这就是希尔排序。

上代码：

void shellSort(vector<int>& intVe) {
	unsigned stepValue = 1;
	size_t vsize = intVe.size();
	while (3 * stepValue < vsize) { stepValue = stepValue * 3 + 1; }//h = 1,4,13,40...... 
	while (stepValue >= 1) {
		for (unsigned i = stepValue; i < vsize; ++i) {
			for (unsigned j = i; j >= stepValue && intVe[j] < intVe[j - stepValue]; j -= stepValue) {
				swap(intVe[j], intVe[j - stepValue]);
			}
		}
		stepValue /= 3;
	}
}

希尔排序的时间复杂度主要和h相关，目前最好的h增量序列是Sedgewick 提出的增量序列。
公式为：
$$
hi=max(9?4j?9?2j+1,4k?3?2k+1)
$$
具体数据为：
1，5，19，41，109，209，505，929，2161，3905，8929，16001，36289，64769，146305，260609，587521，1045505，2354689，4188161，9427969，16764929，37730305，67084289，150958081，268386305，603906049，1073643521

可以直接打表

鸣谢：Algorithm(4th)

插入排序及其细节改进与希尔排序

原文：https://www.cnblogs.com/lda-ovo/p/14769015.html