来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/rotate-image
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
这个题目看了会,只想到了先解决局部再解决整体。然后不会了。
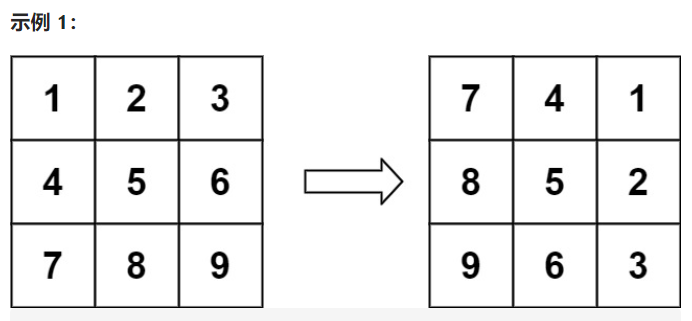
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
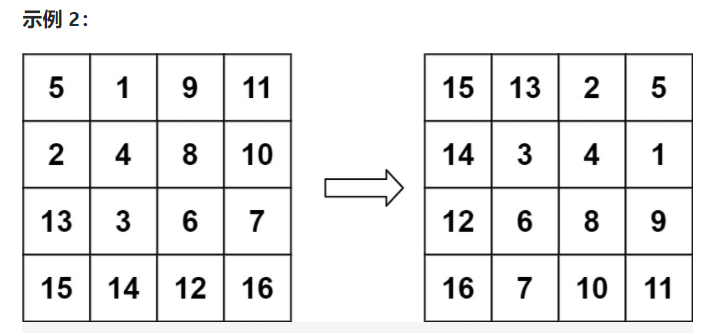
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
作者:zuo-ni-ai-chi-de-tang-seng-rou
链接:https://leetcode-cn.com/problems/rotate-image/solution/li-kou-48xiao-bai-du-neng-kan-dong-de-fang-fa-zhu-/
来源:力扣(LeetCode)
采用分层来进行平移的方式,将矩阵的每一层都分开进行旋转,比如5*5的矩阵可以分为3层
第二次旋转的时候比第一次旋转偏移了一格,这里我们使用add变量来记录矩阵块的偏移量,首先不考虑偏移量的时候写出左上角的坐标为(pos1,pos1),右上角的坐标为(pos1,pos2),左下角的坐标为(pos2,pos1),右下角的坐标为(pos2,pos2),则能够写出偏移之后对应的坐标
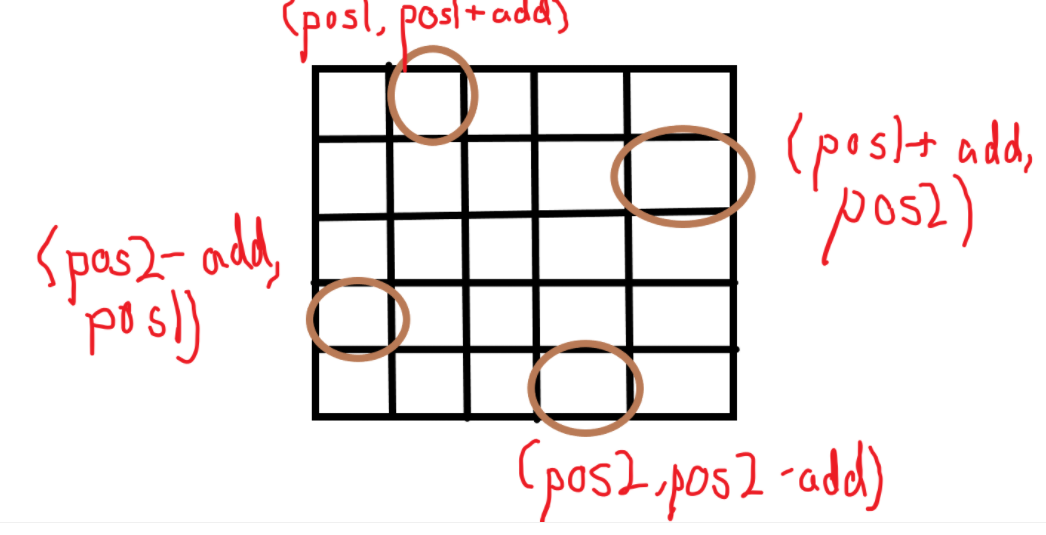
每次计算完一层之后,矩阵向内收缩一层,所以有pos1 = pos1+1,pos2 = pos2-1,终止的条件为pos1 < pos2
1 class Solution: 2 def rotate(self, matrix: List[List[int]]) -> None: 3 pos1,pos2 = 0,len(matrix)-1 4 while pos1<pos2: 5 add = 0 6 while add < pos2-pos1: 7 #左上角为0块,右上角为1块,右下角为2块,左下角为3块 8 temp = matrix[pos2-add][pos1] 9 matrix[pos2-add][pos1] = matrix[pos2][pos2-add] 10 #3 = 2 11 matrix[pos2][pos2-add] = matrix[pos1+add][pos2] 12 #2 = 1 13 matrix[pos1+add][pos2] = matrix[pos1][pos1+add] 14 #1 = 0 15 matrix[pos1][pos1+add] = temp 16 #0 = temp 17 add = add+1 18 pos1 = pos1+1 19 pos2 = pos2-1 20 21 作者:zuo-ni-ai-chi-de-tang-seng-rou 22 链接:https://leetcode-cn.com/problems/rotate-image/solution/li-kou-48xiao-bai-du-neng-kan-dong-de-fang-fa-zhu-/ 23 来源:力扣(LeetCode)
原文:https://www.cnblogs.com/Harukaze/p/14771344.html