路径规划算法-动态规划算法

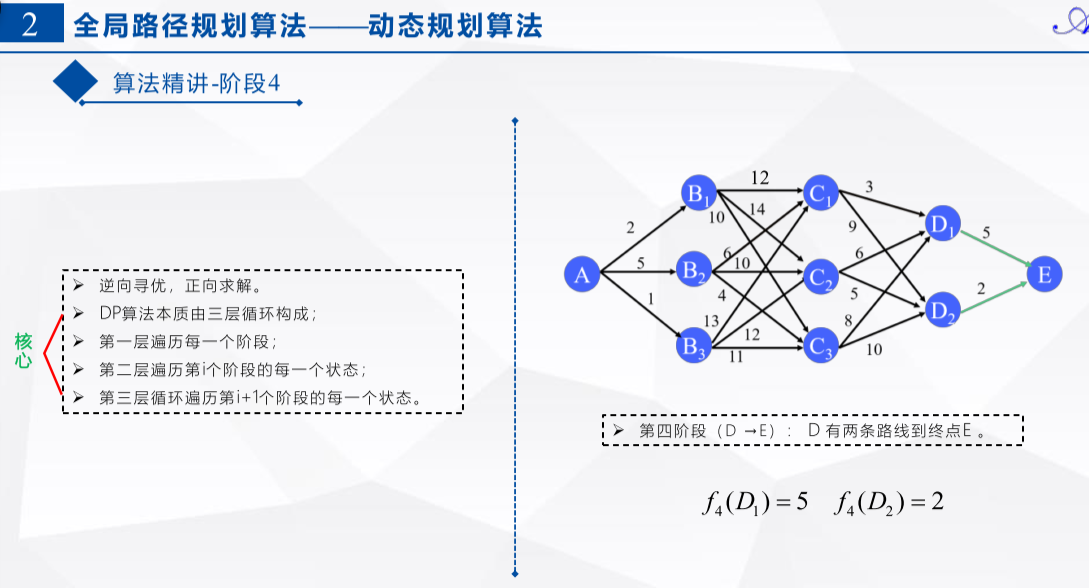
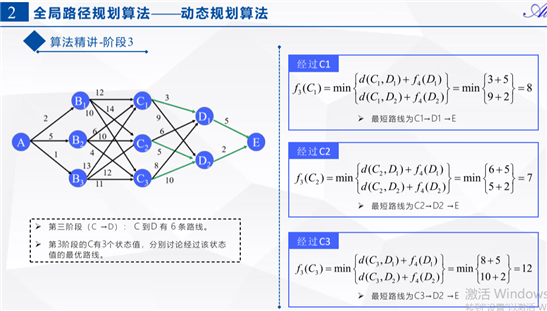
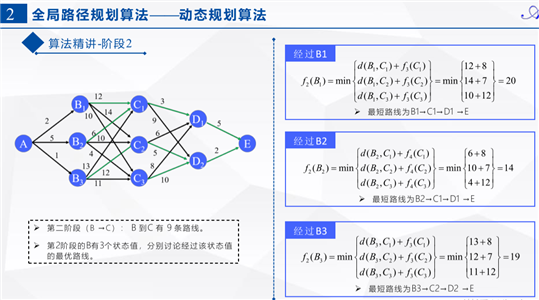
clc
clear
close all

%% 阶段-状态定义
stages = 5;
nodes_dist = cell(stages-1,3);

% 第1阶段
nodes_dist{1,1} = 1;
nodes_dist{1,2} = [1,2,3];
nodes_dist{1,3} = [2,5,1];

% 第2阶段
nodes_dist{2,1} = [1;2;3];
nodes_dist{2,2} = [1,2,3];
nodes_dist{2,3} = [12, 14, 10; 6, 10, 4; 13, 12, 11];

% 第3阶段
nodes_dist{3,1} = [1;2;3];
nodes_dist{3,2} = [1,2];
nodes_dist{3,3} = [3, 9; 6, 5; 8, 10];

% 第4阶段
nodes_dist{4,1} = [1;2];
nodes_dist{4,2} = 1;
nodes_dist{4,3} = [5; 2];

% 第4阶段
nodes_dist{5,1} = 1;
nodes_dist{5,2} = 1;
nodes_dist{5,3} = 0;

% 最优路径及其距离值定义
path = cell(stages, 1);
dist = cell(stages, 1);
for i = 1:stages-1
    dist{i, 1} = nodes_dist{i,1};
    dist{i, 2} = inf(length(dist{i, 1}), 1);
    path{i, 1} = nodes_dist{i,1};
end
dist{stages, 1} = 1;  
dist{stages, 2} = 0;  
path{stages, 1} = 1;
path{stages, 2} = 1;
% 根据最后一个阶段，直接初始化

%% 逆向寻优

% 第一层循环：逆向遍历每一个阶段
for i = stages-1:-1:1
    num_states_f = length(nodes_dist{i, 1});    

    % 第二层循环：遍历第i阶段的每一个状态
    for j = 1:num_states_f
        num_states_r = length(nodes_dist{i+1, 1});        
        
        % 第三层循环：遍历第i阶段的第j个状态到第i+1阶段的每一条路径
        for k = 1:num_states_r
            if  nodes_dist{i,3}(j,k) + dist{i+1,2}(k,1) < dist{i,2}(j,1)  %只保留每种状态的最短路径及最短距离
                dist{i,2}(j,1) = nodes_dist{i,3}(j,k) + dist{i+1,2}(k,1);
                path{i, 2}(j,:) = [j, path{i+1, 2}(k,:)];
            end
        end
    end
end
            
%% 正向求解
path_opt =  path(1,1);    
dist_opt =  dist{1,2};