在所谓二叉树搜索树(binary search tree)中,处处都满足顺序性:
任一节点 r 左右子树中,所有节点(若存在)均不大于(不小于) r
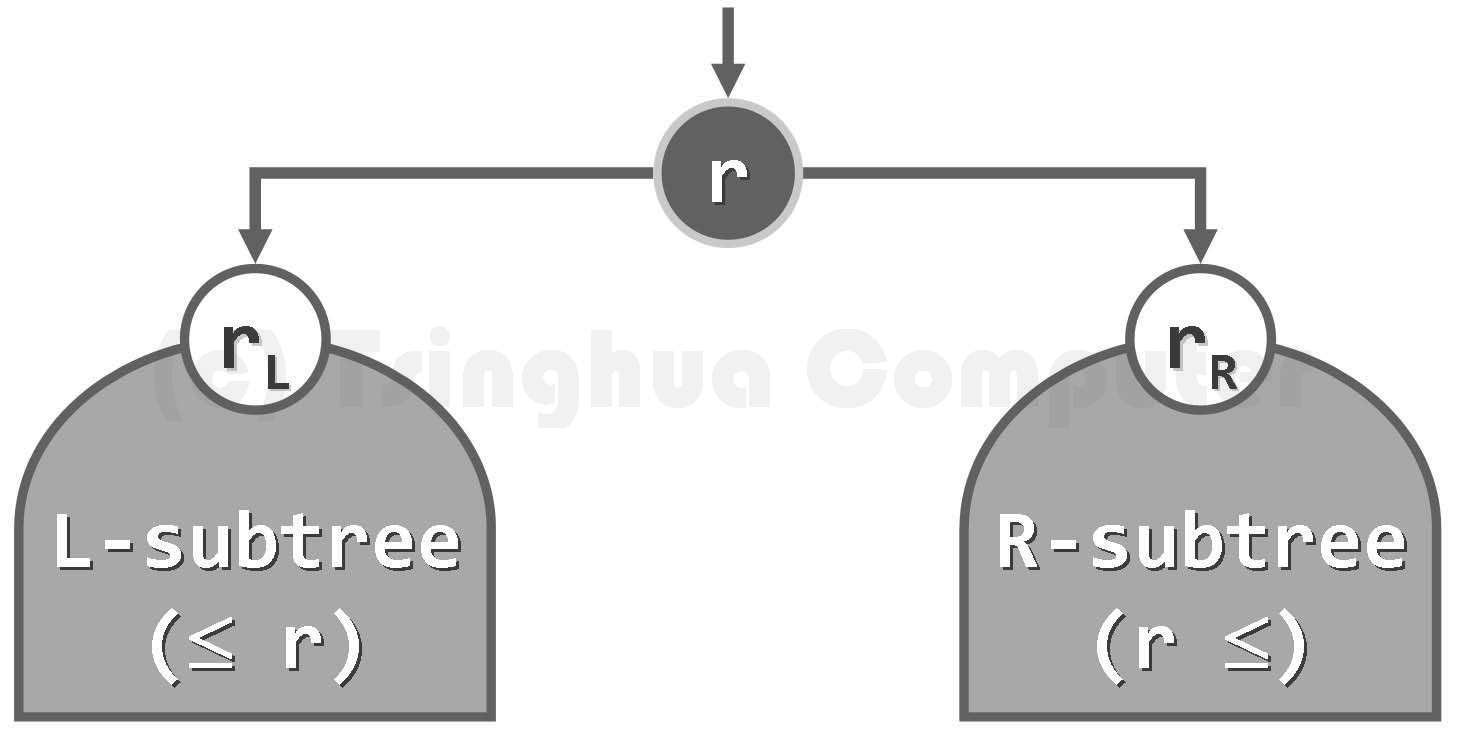
上述顺序性可简化表述为:任一节点的左右子树中,所有节点(若存在)均小于(大于) r

二叉搜索树的三个实例(左),三个反例(右)
二叉搜索树的中序遍历序列必然单调非降
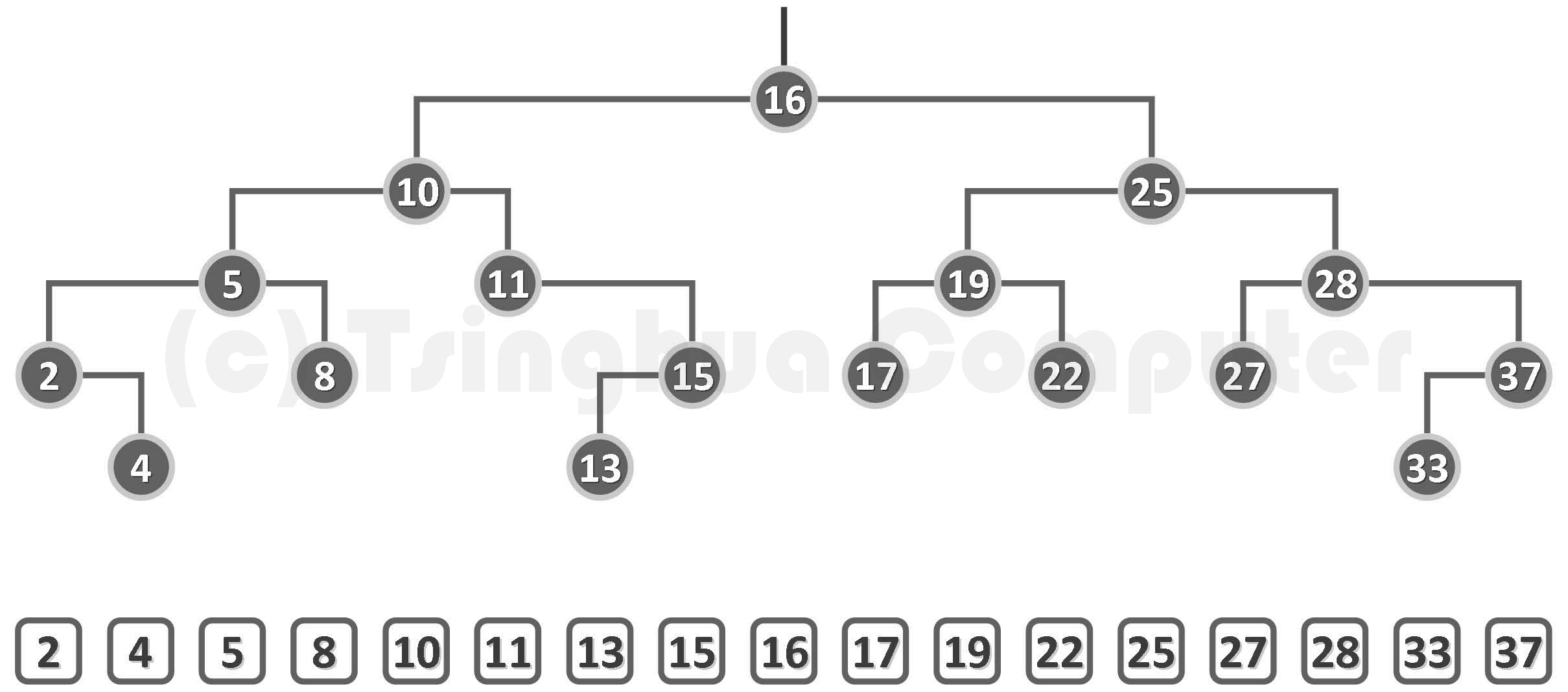
二叉搜索树属于二叉树的特列,所以基于二叉树模板类BinTree可以派生出BST模板类
1 template<typename T> 2 class BST :public BinTree<T> 3 { 4 protected: 5 TreeNode<T>* _hot; //“命中”节点的父亲 6 void insertAsLc(TreeNode<T>* p, T const& e) = delete; 7 void insertAsRc(TreeNode<T>* p, T const& e) = delete; 8 void insertAsRoot(T const& e) = delete; 9 //在以p为根节点的BST中查找关键码e 10 TreeNode<T>*& _search(TreeNode<T>*& p, const T& e, TreeNode<T>*& hot); 11 //删除x所指示的节点 12 TreeNode<T>* _remove(TreeNode<T>*& x, TreeNode<T>*& hot); 13 //“3+4”重构 14 TreeNode<T>* _connect34(TreeNode<T>* a, TreeNode<T>* b, TreeNode<T>* c, 15 TreeNode<T>* T0, TreeNode<T>* T1, TreeNode<T>* T2, TreeNode<T>* T3); 16 //AVL树重平衡 17 TreeNode<T>* _rotateAt(TreeNode<T>* v); 18 public: 19 BST() :_hot(nullptr) {} 20 //在树中查找关键码e 21 virtual TreeNode<T>*& search(const T& e) 22 { 23 return _search(BinTree<T>::_root, e, _hot); 24 } 25 //将关键码插入BST中 26 virtual TreeNode<T>* insert(const T& e); 27 //删除关键码e 28 virtual bool remove(const T& e); 29 };
二叉搜索树的查找算法基于减而治之的思路与策略,其执行过程可以描述为:
从树根出发,逐步地缩小查找范围,直到发现目标(成功)或缩小至空树(失败)
二叉搜索树的查找类似如下过程:
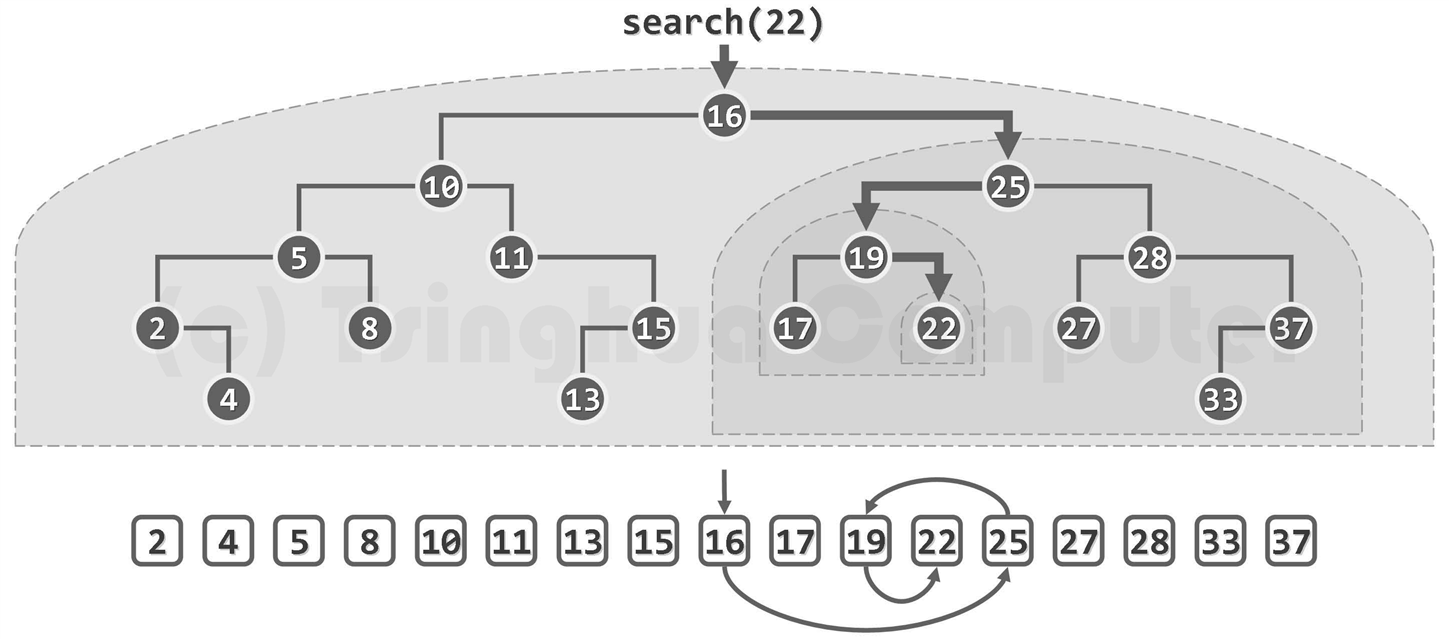
一般地,在查找过程中,一旦发现当前节点为空,即说明查找范围已缩小至空,查找失败。
对照中序遍历序列可见,整个过程与有序向量的二分查找过程等效,故可视作后者的推广。
template<typename T> TreeNode<T>*& BST<T>::_search(TreeNode<T>*& p, const T& e, TreeNode<T>*& hot) { //递归基:命中节点或查找失败 if (!p || p->_val == e)return p; hot = p; //一般情况,记下当前节点,深入一层,递归查找 return _search(((e < p->_val) ? p->_left : p->_right), e, hot); //返回值指向命中节点(或是假想的哨兵),hot指向其父节点(退化时为初始值nullptr) }
节点的插入和删除操作,都需要先调用查找算法,依据查找结果决定后续的处理方式,所以此处以引用方式传递(子)树根节点,以为后续操作提供必要信息。
以上查找算法之所以如此实现,是为了统一并简化后续不同搜索树的各种操作接口的实现。其中的技巧,主要体现于返回值和 hot 变量。
若查找成功,则search()的返回值指向一个关键码为e且真实存在的节点;若查找失败,则返回值的数值虽然为nullptr,但可以假象地将此空节点转换为一个数值为e的哨兵节点,如此,无论成功与否,查找的返回值总是等效地指向“命中节点”。
在整个查找过程中,hot变量始终指向当前节点的父亲。因此在算法返回时,按照如上定义,_hot将指向“命中节点”的父亲。_hot节点是否拥有另一个孩子,与查找成功与否无关,查找成功时,节点e可能是叶子,也可能是内部节点;查找失败时,假想的哨兵节点e等效于叶节点,但可能有兄弟。
在删除操作中,也要首先进行查找,按照以上语义,命中节点必然是待摘除节点:该节点与其父亲节点 _hot 联合指示了删除操作的位置。
在插入操作中,“命中节点”就是待插入的新节点,而 _hot 所指向的,就是该节点可行的插入位置
在二叉搜索树的每一层,查找算法至多访问一个节点,且只需常数时间,故总体所需时间应线性正比于查找路径的长度,或最终返回节点的深度。在最好情况下,目标关键码恰好出现在树根处(或其附近),此时只需O(1)时间。然而对于规模为 n 的二叉搜索树,深度在最坏情况下可达Ω(n)。比如当该树退化为(接近于)一条单链时,发生此类情况的概率将很高。
由此我们可以得到启示:若要控制单次查找在最坏情况下的运行时间,须从控制二叉搜索树的高度入手。
为了在二叉搜索树中插入一个新节点,需要首先利用查找算法确定插入的位置及方向,然后将新节点作为叶子插入。
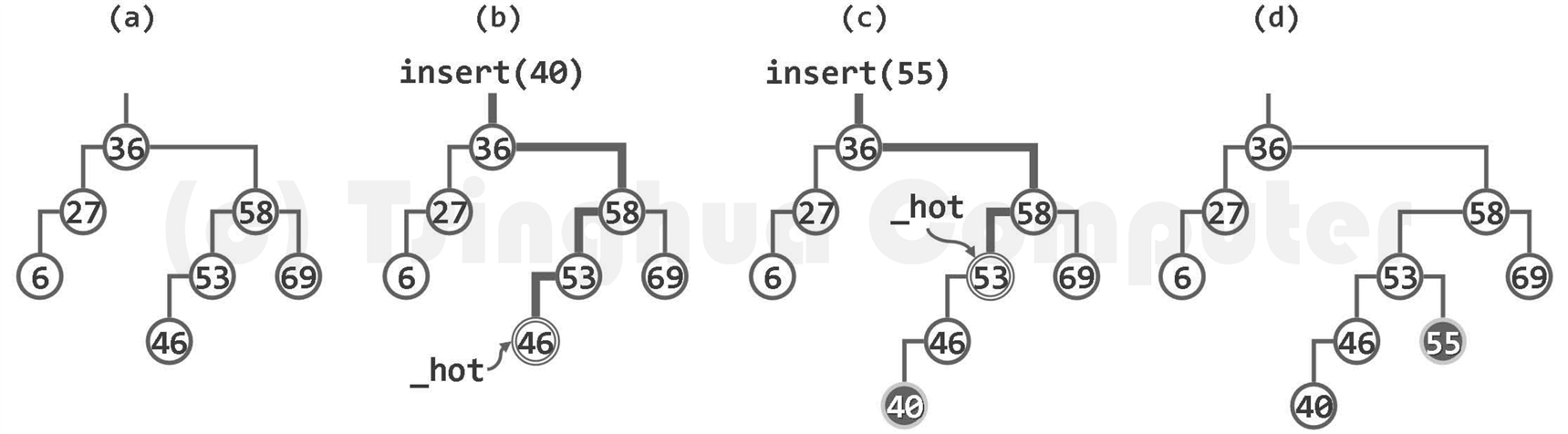
在插入一个节点之后,还需从节点 _hot 出发,自下而上地逐个更新其历代祖先的高度。
1 template<typename T> 2 TreeNode<T>* BST<T>::insert(const T& e) 3 { 4 TreeNode<T>*& p = search(e);//定位插入位置 5 if (!p) //确定目标不存在 6 { 7 //以_hot为父亲节点创建新节点 8 p = new TreeNode<T>(e, _hot); 9 ++BinTree<T>::_size; //更新树的规模 10 this->_updateHeightAbove(p); 11 //最后更新其历代祖先的高度 12 } 13 return p; 14 //无论e是否存在于树中,返回时总有p->_val == e 15 }
为从二叉树中删除节点,首先也需要查找以确定目标接待节点的确存在于树中。
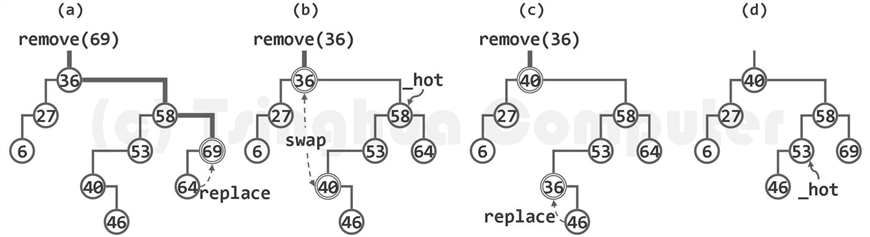
以上图为例,为了删除节点 69 ,只需将该节点替换为其左子节点 64 , 拓扑意义上的节点删除即告完成。当然,还需自下而上地更新节点 64 历代祖先的高度。首个需要更新高度的节点 58 ,恰好由 _hot 指示。对于没有左孩子的目标节点,也可以对称处理。
还是以上图为例,若要删除节点 36 ,首先调用 succ() 算法, 找到该节点的直接后继 40 ,然后交换二者的数据项,则可将后继节点等效为待删除的目标节点。不难验证,该后继节点必然无左孩子,从而相当于将双分支情况转化为单分支的情况。同样,此时也要更新一系列祖先节点的高度,此时首个需要更新高度的节点也恰好由_hot 指示。
1 template<typename T> 2 bool BST<T>::remove(const T& e) 3 { 4 TreeNode<T>*& x = search(e); 5 //确认目标存在 6 if (!x)return false; 7 //实施删除 8 _remove(x, _hot); --BinTree<T>::_size; 9 //删除成功与否由返回值指示 10 return true; 11 } 12 template<typename T> 13 TreeNode<T>* BST<T>::_remove(TreeNode<T>*& x, TreeNode<T>*& hot) 14 { 15 TreeNode<T>* w = x; 16 //实际被删除的节点 17 TreeNode<T>* succ = nullptr; 18 //实际被删除节点的接替者 19 if (!x->_left)succ = x = x->_right; 20 //若左子树不存在,则直接将其替换为右子树 21 else if (!x->_right)succ = x = x->_left; 22 //对称处理 23 else 24 { //否则 25 w = w->succ(); 26 //找到待删除节点在中序遍历下的后继节点 27 swap(x->_val, w->_val);//交换其数据项 28 TreeNode<T>* u = w->_parent; 29 ((u == x) ? u->_right : u->_left) = succ = w->_right; 30 } 31 hot = w->_parent; //实际被删除节点的父亲 32 if (succ)succ->_parent = hot; //被删除节点的接替者与hot相联 33 delete w; 34 return succ; //返回接替者 35 }
删除操作所需的时间主要消耗与search()、succ()、updateHeightAbove()的调用。在树中任一高度,它们至多消耗O(1)时间。故总体的渐进时间复杂度,亦不超过全树的高度。
原文:https://www.cnblogs.com/sxzh/p/14774014.html