一种更好的方法是利用网络中所有运算都是可微(differentiable)的这一事实,计算损失相对于网络系数的梯度(gradient),然后向梯度的反方向改变系数,从而使损失降低。
假设有一个连续的光滑函数 f(x) = y,将实数 x 映射为另一个实数 y。由于函数是连续的,x 的微小变化只能导致 y 的微小变化——这就是函数连续性的直观解释。假设 x 增大了一个很小的因子 epsilon_x,这导致 y 也发生了很小的变化,即 epsilon_y:
f(x + epsilon_x) = y + epsilon_y
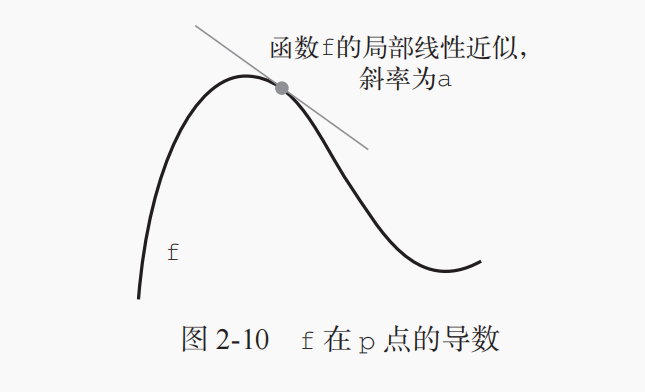
此外,由于函数是光滑的(即函数曲线没有突变的角度),在某个点 p 附近,如果 epsilon_x足够小,就可以将 f 近似为斜率为 a 的线性函数,这样 epsilon_y 就变成了 a * epsilon_x:
f(x + epsilon_x) = y + a * epsilon_x
显然,只有在 x 足够接近 p 时,这个线性近似才有效。斜率 a 被称为 f 在 p 点的导数(derivative)。如果 a 是负的,说明 x 在 p 点附近的微小变化将导致 f(x) 减小(如图 2-10 所示);如果 a 是正的,那么 x 的微小变化将导致 f(x) 增大。此外,a 的绝对值(导数大小)表示增大或减小的速度快慢。
对于每个可微函数 f(x)(可微的意思是“可以被求导”。例如,光滑的连续函数可以被求导),都存在一个导数函数 f‘(x),将 x 的值映射为 f 在该点的局部线性近似的斜率。例如,cos(x)的导数是 -sin(x),f(x) = a * x 的导数是 f‘(x) = a,等等。
如果你想要将 x 改变一个小因子 epsilon_x,目的是将 f(x) 最小化,并且知道 f 的导数,那么问题解决了:导数完全描述了改变 x 后 f(x) 会如何变化。如果你希望减小 f(x) 的值,只需将 x 沿着导数的反方向移动一小步。
2.张量运算的导数:梯度
梯度是张量运算的导数。它是导数向多元函数导数的推广。多元函数以张量作为输入的函数。
例:假设有一个输入向量 x、一个矩阵 W、一个目标 y 和一个损失函数 loss。你可以用 W 来计算预测值 y_pred,然后计算损失,或者说预测值 y_pred 和目标 y 之间的距离。
y_pred = dot(W, x)
loss_value = loss(y_pred, y)
假设输入数据x和y不变,那么这可以看做将w映射到损失值的函数
前面已经看到,单变量函数 f(x) 的导数可以看作函数 f 曲线的斜率。同样,gradient(f)(W0) 也可以看作表示 f(W) 在 W0 附近曲率(curvature)的张量。
3.随机梯度下降
给定一个可微函数,理论上可以用解析法找到它的最小值:函数的最小值是导数为 0 的点,因此你只需找到所有导数为 0 的点,然后计算函数在其中哪个点具有最小值。
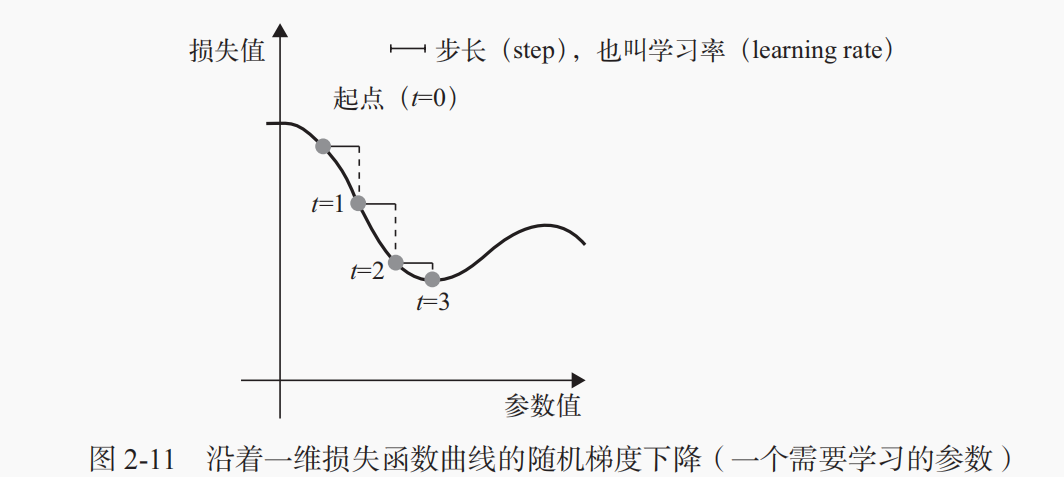
小批量随机梯度下降:
(1) 抽取训练样本 x 和对应目标 y 组成的数据批量。
(2) 在 x 上运行网络,得到预测值 y_pred。
(3) 计算网络在这批数据上的损失,用于衡量 y_pred 和 y 之间的距离。
(4) 计算损失相对于网络参数的梯度[一次反向传播(backward pass)]。
(5) 将参数沿着梯度的反方向移动一点
注:随机是指每批数据都是随机抽取的
真SGD:每次迭代时只抽取一个样本和目标,而不是抽取一批数据
批量SGD:每一次迭代都在所有数据上运行
其他变体:带动量的SGD,Adagrad、RMSProp等变体
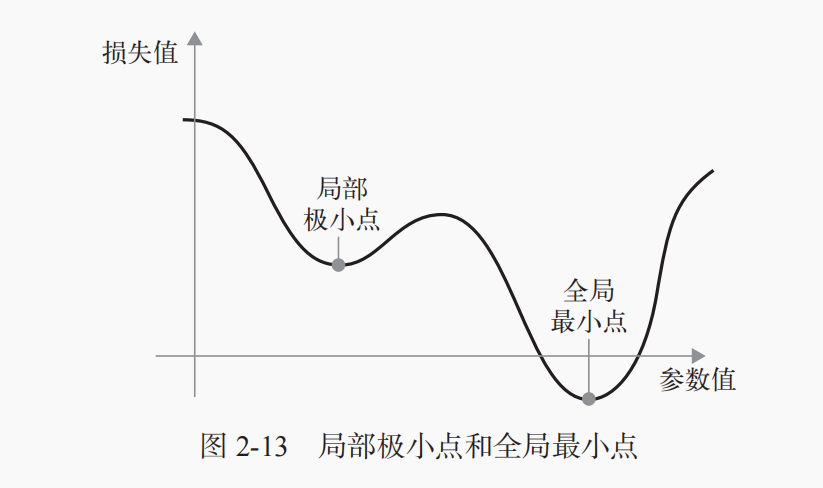
如你所见,在某个参数值附近,有一个局部极小点(local minimum):在这个点附近,向左移动和向右移动都会导致损失值增大。如果使用小学习率的 SGD 进行优化,那么优化过程可能会陷入局部极小点,导致无法找到全局最小点。
动量方法简单实现:
past_velocity = 0.
momentum = 0.1
while loss > 0.01:
w, loss, gradient = get_current_parameters()
velocity = past_velocity * momentum - learning_rate * gradient
w = w + momentum * velocity - learning_rate * gradient
past_velocity = velocity
update_parameter(w)
4.链式求导:反向传播算法
在前面的算法中,我们假设函数是可微的,因此可以明确计算其导数。在实践中,神经网络函数包含许多连接在一起的张量运算,每个运算都有简单的、已知的导数。例如,下面这个网络 f 包含 3 个张量运算 a、b 和 c,还有 3 个权重矩阵 W1、W2 和 W3。
f(W1, W2, W3) = a(W1, b(W2, c(W3)))
根据微积分的知识,这种函数链可以利用下面这个恒等式进行求导,它称为链式法则(chain rule):(f(g(x)))‘ = f‘(g(x)) * g‘(x)。将链式法则应用于神经网络梯度值的计算,得到的算法叫作反向传播(backpropagation,有时也叫反式微分,reverse-mode differentiation)。反向传播从最终损失值开始,从最顶层反向作用至最底层,利用链式法则计算每个参数对损失值的贡献大小。
现在以及未来数年,人们将使用能够进行符号微分(symbolic differentiation)的现代框架来实现神经网络,比如 TensorFlow。也就是说,给定一个运算链,并且已知每个运算的导数,这些框架就可以利用链式法则来计算这个运算链的梯度函数,将网络参数值映射为梯度值。对于这样的函数,反向传播就简化为调用这个梯度函数。由于符号微分的出现,你无须手动实现反向传播算法。