算法分类
常见算法可以分为两大类:
非线性时间比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此称为非线性时间比较类排序。
线性时间非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。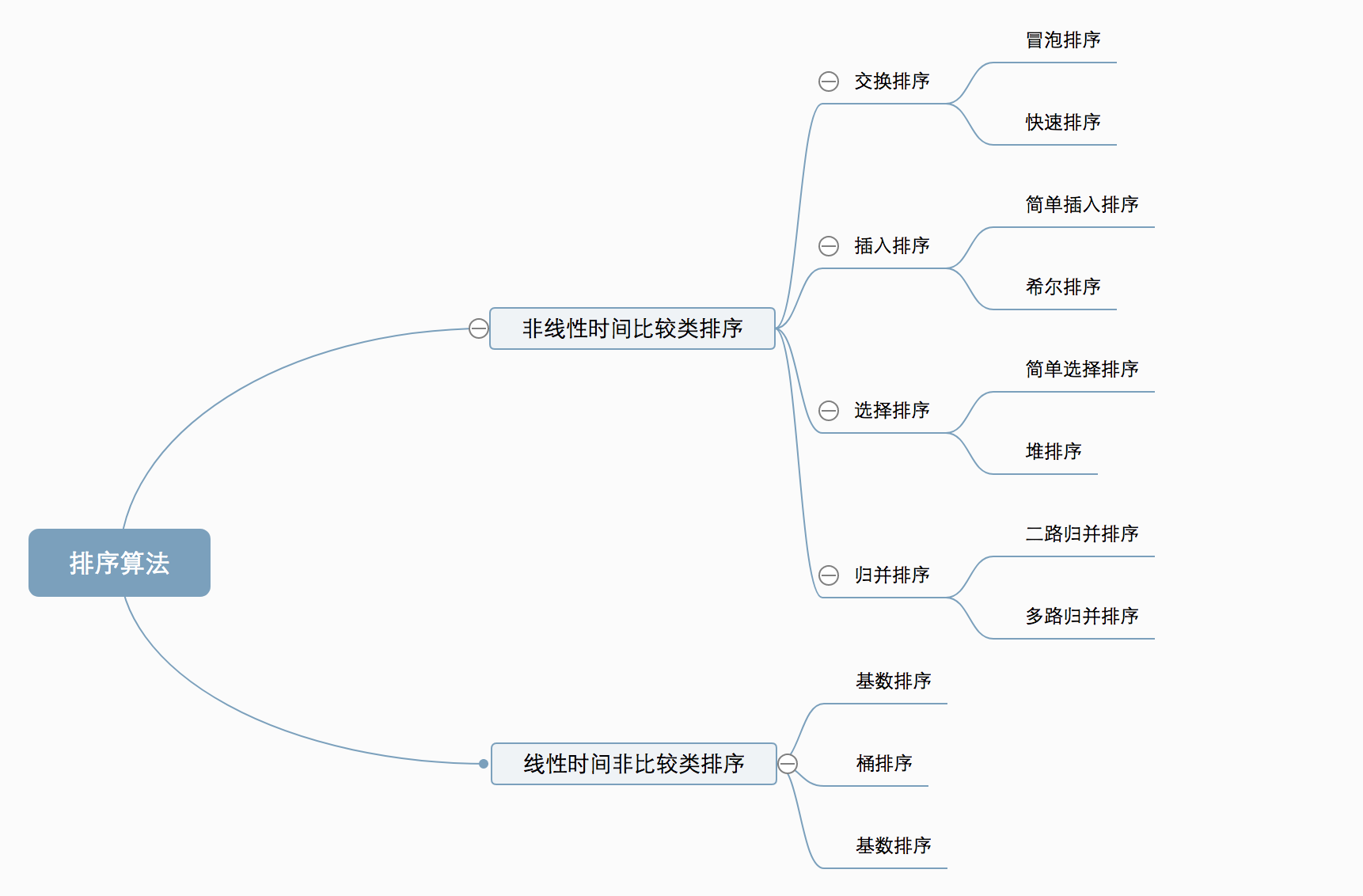
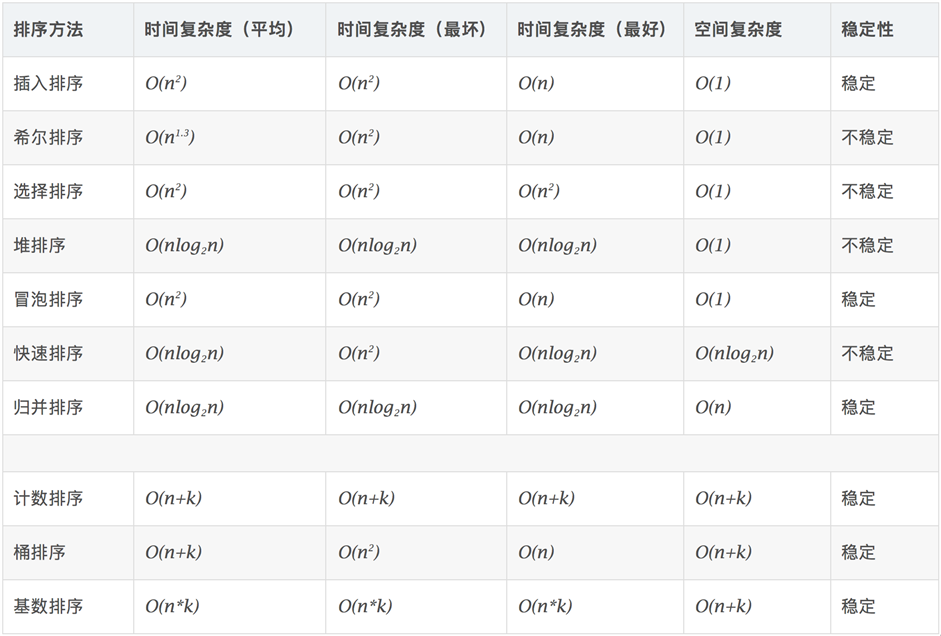
算法复杂度:
1、冒泡排序
思路:外层循环从1到n-1,内循环从当前外层的元素的下一个位置开始,依次和外层的元素比较,出现逆序就交换,通过与相邻元素的比较和交换来把小的数交换到最前面。
1 for(int i=0;i<arr.length-1;i++){//外层循环控制排序趟数
2 for(int j=0;j<arr.length-1-i;j++){//内层循环控制每一趟排序多少次
3 if(arr[j]>arr[j+1]){
4 int temp=arr[j];
5 arr[j]=arr[j+1];
6 arr[j+1]=temp;
7 }
8 }
9 }
2、选择排序
思路:冒泡排序是通过相邻的比较和交换,每次找个最小值。选择排序是:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
1 private static void sort(int[] array) {
2 int n = array.length;
3 for (int i = 0; i < n-1; i++) {
4 int min = i;
5 for (int j = i+1; j < n; j++) {
6 if (array[j] < array[min]){//寻找最小数
7 min = j; //将最小数的索引赋值
8 }
9 }
10 int temp = array[i];
11 array[i] = array[min];
12 array[min] = temp;
13
14 }
15 }
16
3、插入排序
思路:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。可以理解为玩扑克牌时的理牌;
1 private static void sort(int[] array) {
2 int n = array.length;
3 /**
4 *从第二位数字开始,每一个数字都试图跟它的前一个比较并交换,并重复;直到前一个数字不存在或者比它小或相等时停下来
5 **/
6 for (int i = 1; i < n; i++) {//从第二个数开始
7 int key = array[i];
8 int j = i -1;
9 while (j >= 0 && array[j]>key) {
10 array[j + 1] = array[j]; //交换
11 j--; //下标向前移动
12 }
13 array[j+1] = key;
14 }
15 }
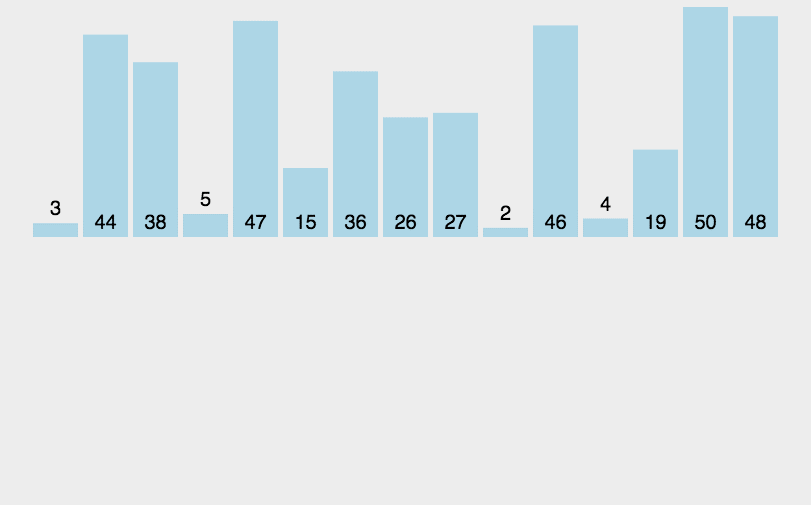
4、希尔排序
思路:希尔排序是插入排序的一种高效率的实现,也叫缩小增量排序。先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时再对全体记录进行一次直接插入排序。
问题:增量的序列取法?
关于取法,没有统一标准,但最后一步必须是1;因为不同的取法涉及时间复杂度不一样,具体了解可以参考《数据结构与算法分析》;一般以length/2为算法。(再此以gap=gap*3+1为公式)
1 private static void sort(int[] array) {
2 int n = array.length;
3 int h = 1;
4 while (h<n/3) { //动态定义间隔序列
5 h = 3*h +1;
6 }
7 while (h >= 1) {
8 for (int i = h; i < n; i++) {
9 for (int j = i; j >= h && (array[j] < array[j - h]); j -= h) {
10 int temp = array[j];
11 array[j] = array[j - h];
12 array[j-h]= temp;
13 }
14 }
15 h /=3;
16 }
17 }
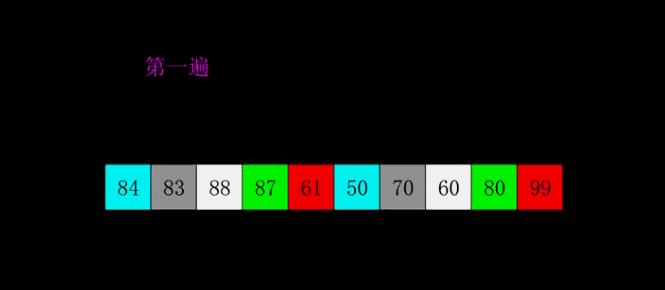
5、归并排序
思路:将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。它使用了递归分治的思想;相当于:左半边用尽,则取右半边元素;右半边用尽,则取左半边元素;右半边的当前元素小于左半边的当前元素,则取右半边元素;右半边的当前元素大于左半边的当前元素,则取左半边的元素。
自顶向下:
1 private static void mergeSort(int[] array) {
2 int[] aux = new int[array.length];
3 sort(array, aux, 0, array.length - 1);
4 }
5
6 private static void sort(int[] array, int[] aux, int lo, int hi) {
7 if (hi<=lo) return;
8 int mid = lo + (hi - lo)/2;
9 sort(array, aux, lo, mid);
10 sort(array, aux, mid + 1, hi);
11 merge(array, aux, lo, mid, hi);
12 }
13
14 private static void merge(int[] array, int[] aux, int lo, int mid, int hi) {
15 System.arraycopy(array,0,aux,0,array.length);
16 int i = lo, j = mid + 1;
17 for (int k = lo; k <= hi; k++) {
18 if (i>mid) array[k] = aux[j++];
19 else if (j > hi) array[k] = aux[i++];
20 else if (aux[j]<aux[i]) array[k] = aux[j++];
21 else array[k] = aux[i++];
22 }
23 }
自底向上:
1 public static void sort(int[] array) {
2 int N = a.length;
3 int[] aux = new int[N];
4 for (int n = 1; n < N; n = n+n) {
5 for (int i = 0; i < N-n; i += n+n) {
6 int lo = i;
7 int m = i+n-1;
8 int hi = Math.min(i+n+n-1, N-1);
9 merge(array, aux, lo, m, hi);
10 }
11 }
12 }
13
14 private static void merge(int[] array, int[] aux, int lo, int mid, int hi) {
15 for (int k = lo; k <= hi; k++) {
16 aux[k] = array[k];
17 }
18 // merge back to a[]
19 int i = lo, j = mid+1;
20 for (int k = lo; k <= hi; k++) {
21 if (i > mid) array[k] = aux[j++]; // this copying is unneccessary
22 else if (j > hi) array[k] = aux[i++];
23 else if (aux[j]<aux[i]) array[k] = aux[j++];
24 else array[k] = aux[i++];
25 }
26 }
缺点:因为是Out-place sort,因此相比快排,需要很多额外的空间。
为什么归并排序比快速排序慢?
答:虽然渐近复杂度一样,但是归并排序的系数比快排大。
对于归并排序有什么改进?
答:就是在数组长度为k时,用插入排序,因为插入排序适合对小数组排序。在算法导论思考题2-1中介绍了。复杂度为O(nk+nlg(n/k)) ,当k=O(lgn)时,复杂度为O(nlgn)
例子:
1 private static int mark = 0;
2 /**
3 * 归并排序
4 */
5 private static int[] sort(int[] array, int low, int high) {
6 int mid = (low + high) / 2;
7 if (low < high) {
8 mark++;
9 System.out.println("正在进行第" + mark + "次分隔,得到");
10 System.out.println("[" + low + "-" + mid + "] [" + (mid + 1) + "-" + high + "]");
11 // 左边数组
12 sort(array, low, mid);
13 // 右边数组
14 sort(array, mid + 1, high);
15 // 左右归并
16 merge(array, low, mid, high);
17 }
18 return array;
19 }
20
21 /**
22 * 对数组进行归并
23 *
24 * @param array
25 * @param low
26 * @param mid
27 * @param high
28 */
29 private static void merge(int[] array, int low, int mid, int high) {
30 System.out.println("合并:[" + low + "-" + mid + "] 和 [" + (mid + 1) + "-" + high + "]");
31 int[] temp = new int[high - low + 1];
32 int i = low;// 左指针
33 int j = mid + 1;// 右指针
34 int k = 0;
35 // 把较小的数先移到新数组中
36 while (i <= mid && j <= high) {
37 if (array[i] < array[j]) {
38 temp[k++] = array[i++];
39 } else {
40 temp[k++] = array[j++];
41 }
42 }
43 // 两个数组之一可能存在剩余的元素
44 // 把左边剩余的数移入数组
45 while (i <= mid) {
46 temp[k++] = array[i++];
47 }
48 // 把右边边剩余的数移入数组
49 while (j <= high) {
50 temp[k++] = array[j++];
51 }
52 // 把新数组中的数覆盖array数组
53 for (int m = 0; m < temp.length; m++) {
54 array[m + low] = temp[m];
55 }
56 }
57
58 /**
59 * 归并排序
60 */
61 public static int[] sort(int[] array) {
62 return sort(array, 0, array.length - 1);
63 }
64
65 public static void main(String[] args) {
66 int[] array = { 3, 5, 2, 6, 2 };
67 int[] sorted = sort(array);
68 System.out.println("最终结果");
69 for (int i : sorted) {
70 System.out.print(i + " ");
71 }
72 }
6、快速排序
思路:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
private static void sort(int[] array) {
shuffle(array);
sort(array, 0, array.length - 1);
}
private static void sort(int[] array, int lo, int hi) {
if(hi<=lo+M) {
Insert.sort(a,lo,hi);
return;
}
int lt = lo, gt = hi;
int v = array[lo];
int i = lo;
while (i <= gt) {
if (array[i]<v) exch(array, lt++, i++);
else if (array[i]>v) exch(array, i, gt--);
else i++;
}
// a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi].
sort(array, lo, lt-1);
sort(array, gt+1, hi);
}
private static void exch(int[] a, int i, int j) {
int swap = a[i];
a[i] = a[j];
a[j] = swap;
}
/**
*打乱数组
*/
private static void shuffle(int[] array) {
Random random = new Random(System.currentTimeMillis());
if (array == null) throw new NullPointerException("argument array is null");
int n = array.length;
for (int i = 0; i < n; i++) {
int r = i + random.nextInt(n-i); // between i and n-1
int temp = array[i];
array[i] = array[r];
array[r] = temp;
}
}
代码例子:
1 package test;
2
3 public class s {
4 public static void main(String[] args) {
5 int[] arr = { 5,2,4,9,7 };
6 sort(arr, 0, arr.length - 1);
7 }
8 public static void sort(int arr[], int low, int high) {
9 int l = low;
10 int h = high;
11 int k = arr[low];
12 while (l < h) {
13 // 从后往前比较
14 while (l < h && arr[h] >= k ){ // 如果没有比关键值小的,比较下一个,直到有比关键值小的交换位置,然后又从前往后比较
15 h--;// h=6
16 }
17 if (l < h) {
18 int temp = arr[h];
19 arr[h] = arr[l];
20 arr[l] = temp;
21 //进行过一次替换后,没必要将替换后的两值再次比较,所以i++直接下一位与k对比
22 l++;
23 }
24 // 从前往后比较
25 while (l < h && arr[l] <= k) { // 如果没有比关键值大的,比较下一个,直到有比关键值大的交换位置
26 l++;
27 }
28 if (l < h) {
29 int temp = arr[h];
30 arr[h] = arr[l];
31 arr[l] = temp;
32 h--;
33 }
34 // 此时第一次循环比较结束,关键值的位置已经确定了。左边的值都比关键值小,右边的值都比关键值大,但是两边的顺序还有可能是不一样的,进行下面的递归调用
35 }
36 print(arr);
37 System.out.print("l=" + (l + 1) + "h=" + (h + 1) + "k=" + k + "\n");
38 // 递归
39 if (l > low)//先判断l>low再次经行左边排序
40 sort(arr, low, l - 1);// 左边序列。第一个索引位置到关键值索引-1
41 if (h < high)//左边依次排序执行完递归后,弹栈进行右边排序
42 sort(arr, l + 1, high);// 右边序列。从关键值索引+1到最后一个
43 }
44 // 打印数组的方法
45 private static void print(int[] arr) {
46 System.out.print("[");
47 for (int i = 0; i < arr.length; i++) {
48 if (i != (arr.length - 1)) {
49 System.out.print(arr[i] + ",");
50 } else {
51 System.out.print(arr[i] + "]");
52 System.out.println();
53 }
54 }
55 }
56 }
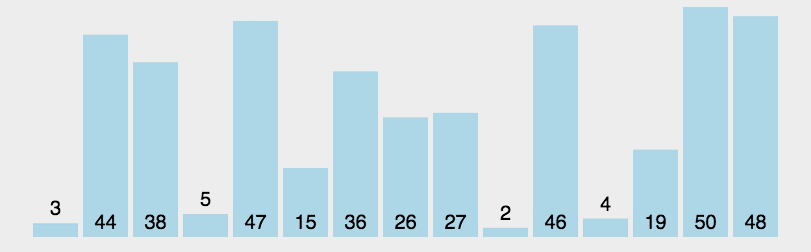
7、堆排序
思路:堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
1 public static void sort(int[] a){
2 int N = a.length;
3 int[] keys = new int[N+1];
4 //注意,堆的数据结构是从1开始的,0不用
5 for (int i = 1; i < keys.length; i++) {
6 keys[i] = a[i-1];
7 }
8 // //构造堆,使得堆是有序的
9 for(int k = N/2;k>=1;k--) sink(keys,k,N);
10 //排序,相当于毁掉堆
11 while(N>1){
12 exch(keys,1,N--);
13 sink(keys,1,N);
14 }
15 //重新写回数组
16 for (int i = 0; i < a.length; i++) {
17 a[i] = keys[i+1];
18 }
19 }
20
21 private static void sink(int[] a, int k, int N) {
22 // TODO Auto-generated method stub
23 while(2*k<=N){
24 int j = 2*k;
25 if (j < N && less(a[j], a[j+1])) j++;
26 if (less(a[j], a[k])) break;
27 exch(a, k, j);
28 k = j;
29 }
30 }
31
32 private static boolean less(int k, int j) {
33 // TODO Auto-generated method stub
34 return k < j;
35 }
36
37 private static void exch(int[] a, int i, int n) {
38 // TODO Auto-generated method stub
39 int temp = a[i];
40 a[i] = a[n];
41 a[n] = temp;
42 }
代码例子:
1 package test;
2
3 public class dui {
4 /**
5 * 调整为小顶堆(排序后结果为从大到小)
6 *
7 * @param array是待调整的堆数组
8 * @param s是待调整的数组元素的位置
9 * @param length是数组的长度
10 *
11 */
12 public static void heapAdjustS(int[] array, int s, int length) {
13 int tmp = array[s];
14 int child = 2 * s + 1;// 左孩子结点的位置
15 System.out.println("待调整结点为:array[" + s + "] = " + tmp);
16 while (child < length) {
17 // child + 1 是当前调整结点的右孩子
18 // 如果有右孩子且小于左孩子,使用右孩子与结点进行比较,否则使用左孩子
19 if (child + 1 < length && array[child] > array[child + 1]) {
20 child++;
21 }
22 System.out.println("将与子孩子 array[" + child + "] = " + array[child] + " 进行比较");
23 // 如果较小的子孩子比此结点小
24 if (array[s] > array[child]) {
25 System.out.println("子孩子比其小,交换位置");
26 array[s] = array[child];// 把较小的子孩子向上移动,替换当前待调整结点
27 s = child;// 待调整结点移动到较小子孩子原来的位置
28 array[child] = tmp;
29 child = 2 * s + 1;// 继续判断待调整结点是否需要继续调整
30
31 if (child >= length) {
32 System.out.println("没有子孩子了,调整结束");
33 } else {
34 System.out.println("继续与新的子孩子进行比较");
35 }
36 // continue;
37 } else {
38 System.out.println("子孩子均比其大,调整结束");
39 break;// 当前待调整结点小于它的左右孩子,不需调整,直接退出
40 }
41 }
42 }
43
44 /**
45 * 调整为大顶堆(排序后结果为从小到大)
46 *
47 * @param array是待调整的堆数组
48 * @param s是待调整的数组元素的位置
49 * @param length是数组的长度
50 *
51 */
52 public static void heapAdjustB(int[] array, int s, int length) {
53 int tmp = array[s];
54 int child = 2 * s + 1;// 左孩子结点的位置
55 System.out.println("待调整结点为:array[" + s + "] = " + tmp);
56 while (child < length) {
57 // child + 1 是当前调整结点的右孩子
58 // 如果有右孩子且大于左孩子,使用右孩子与结点进行比较,否则使用左孩子
59 if (child + 1 < length && array[child] < array[child + 1]) {
60 child++;
61 }
62 System.out.println("将与子孩子 array[" + child + "] = " + array[child] + " 进行比较");
63 // 如果较大的子孩子比此结点大
64 if (array[s] < array[child]) {
65 System.out.println("子孩子比其大,交换位置");
66 array[s] = array[child];// 把较大的子孩子向上移动,替换当前待调整结点
67 s = child;// 待调整结点移动到较大子孩子原来的位置
68 array[child] = tmp;
69 child = 2 * s + 1;// 继续判断待调整结点是否需要继续调整
70
71 if (child >= length) {
72 System.out.println("没有子孩子了,调整结束");
73 } else {
74 System.out.println("继续与新的子孩子进行比较");
75 }
76 // continue;
77 } else {
78 System.out.println("子孩子均比其小,调整结束");
79 break;// 当前待调整结点大于它的左右孩子,不需调整,直接退出
80 }
81 }
82 }
83
84 /**
85 * 堆排序算法
86 *
87 * @param array
88 * @param inverse true 为倒序排列,false 为正序排列
89 */
90 public static void heapSort(int[] array, boolean
