前言

B树和B-树是同一种数据结构，如果不清楚的话，会被面试官忽悠，所以本文介绍两种数据结构，B树和B+树，废话不多数咱们开干。

B树

介绍

在计算机科学中，B树是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数量级的时间复杂度内完成。B树，其实是一颗特殊的二叉查找树（binary search tree），可以拥有多于2个子节点。与自平衡二叉查找树不同，B树为系统大块数据的读写操作做了优化。B树减少定位记录时所经历的中间过程，从而加快存取速度，其实B树主要解决的就是数据IO的问题。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。

特性

一个m阶的B树特点如下：

1. 所有叶子节点都在同一层级；
2. 除了根节点以外的其他节点包含的key值数量在[m/2]-1到m-1的数据范围；
3. 除了根节点和叶子节点外，所有中间节点至少有m/2个孩子节点；
4. 根节点如果不是叶子节点的话，它必须包含至少2个孩子节点；
5. 拥有n-1个key值非叶子节点必须有n个孩子节点；
6. 一个节点的所有key值必须是升序排序的；
   以上六点就是B树的全部特性

检索

在B树种，检索操作类类似于二叉查找树。在二叉查找树中，检索开始于树的根节点，因为是二叉树所以每次有两种选择。在B树种检索中，也是开始于根节点，但每次需要比较n次（n是当前节点的所有子节点的数量）。在B树中，检索操作执行的时间复杂度是O(log n)，检索操作执行如下：

1. 从输入获取读取检索元素；
2. 和根节点的第一个元素进行比较；
3. 如果匹配上，返回元素找到并且终止函数；
4. 如果未匹配上，检查元数据与key值的大小；
5. 如果小于待查元素，继续检索B树的左子树；
6. 如果大于的话，比较相同节点中下一个key值并且重复3、4、5、6步，直到找到指定元素或者在树的叶子节点的最后一个结束；

插入

在B树种的插入操作，新元素一定是新添加在叶子节点的，具体操作流程如下：

1. 检查树是否为空；
2. 如果树为空，用新的插入元素创建一个新的节点并插入到树中并作为树的根节点；
3. 如果树不为空，使用二叉查找树的逻辑为新元素找到一个叶子节点；
4. 如果叶子节点中key有空位置，直接按照叶子节点内key值升序的原则将节点插入；
5. 如果叶子节点中key已经满了，通过发送中间值到父节点，然后分裂叶子节点；重复这个操作，直到发送的中间值存储在一个节点中；
6. 如果分裂发生在根节点，中间值将会成为树的新的根节点，树的高度将会加 1；
   具体操作的演示示例如下所示：
   

删除

1. 如果当前需要删除的key位于非叶子结点上，则用后继key（后继key，即右边叶子节点最左侧即为后继节点）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上，这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步；
2. 该结点key个数大于等于Math.ceil(m/2)-1（向下取整），结束删除操作，否则执行第3步；
3. 如果兄弟结点key个数大于Math.ceil(m/2)-1，则父结点中的key下移到该结点，兄弟结点中的一个key上移，删除操作结束，即从兄弟节点中借一个元素过来；否则，将父结点中的key下移与当前结点及它的兄弟结点中的key合并，形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，重复上第2步。

有些节点它可能即有左兄弟，又有右兄弟，那么我们任意选择一个兄弟结点进行操作即可。
下面以5阶B树为例，介绍B树的删除操作，5阶B树中，结点最多有4个key,最少有2个key

a）原始状态

b）在上面的B树中删除21，删除后结点中的关键字个数仍然大于等2，所以删除结束。

c）在上述情况下接着删除27。从上图可知27位于非叶子结点中，所以用27的后继替换它。从图中可以看出，27的后继为28，我们用28替换27，然后在28（原27）的右孩子结点中删除28。删除后的结果如下图所示。

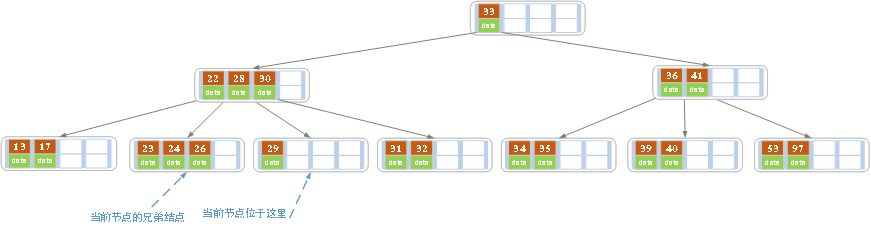
删除后发现，当前叶子结点的记录的个数小于2，而它的兄弟结点中有3个记录（当前结点还有一个右兄弟，选择右兄弟就会出现合并结点的情况，不论选哪一个都行，只是最后B树的形态会不一样而已），我们可以从兄弟结点中借取一个key。所以父结点中的28下移，兄弟结点中的26上移,删除结束。结果如下图所示。

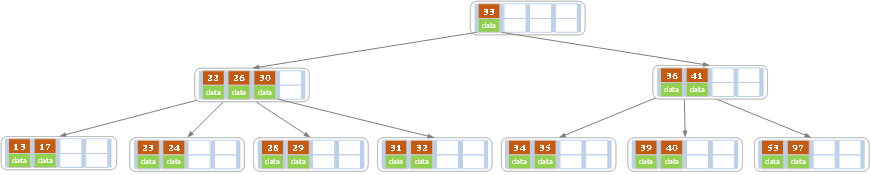
d）在上述情况下接着32，结果如下图。

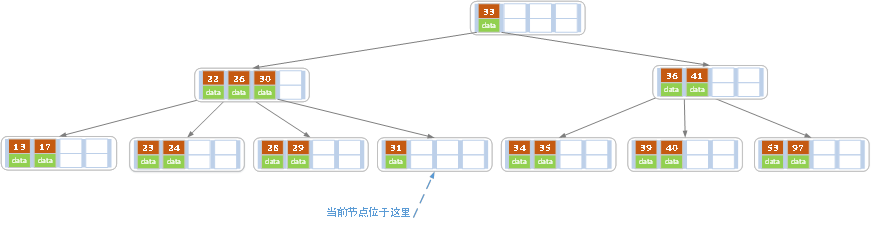
当删除后，当前结点中只key，而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并，成为一个新的结点，当前结点的指针指向父结点。结果如下图所示。

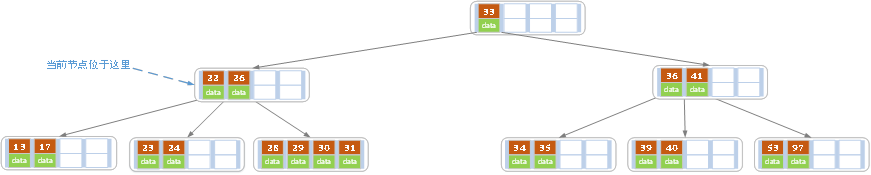
当前结点key的个数满足条件，故删除结束。

e）上述情况下，我们接着删除key为40的记录，删除后结果如下图所示。

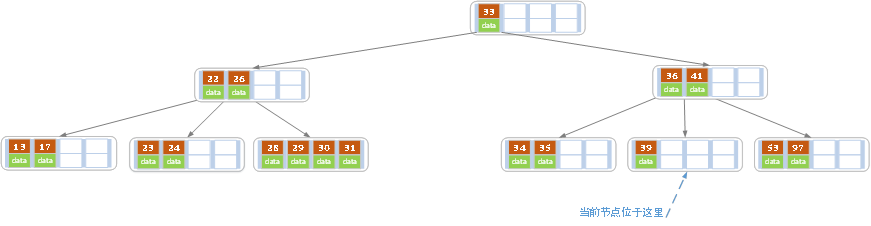
同理，当前结点的记录数小于2，兄弟结点中没有多余key，所以父结点中的key下移，和兄弟（这里我们选择左兄弟，选择右兄弟也可以）结点合并，合并后的指向当前结点的指针就指向了父结点。

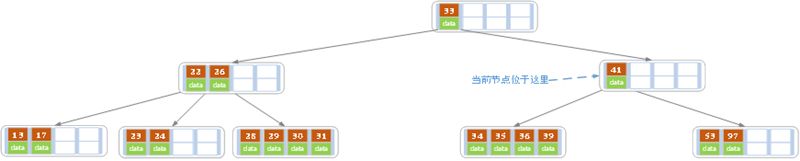
同理，对于当前结点而言只能继续合并了，最后结果如下所示。

合并后结点当前结点满足条件，删除结束。

小结

以上就是B树的特征以及操作过程，应该是说明白了。

B+树

一文完全搞懂B树、B-树、B+树

原文：https://www.cnblogs.com/wxiaotong/p/14781753.html