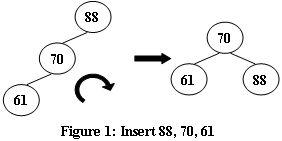
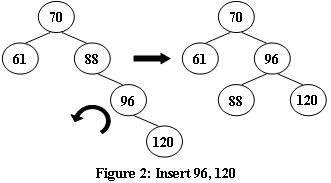
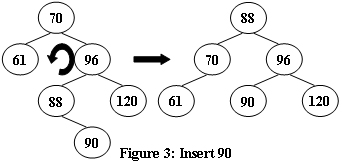
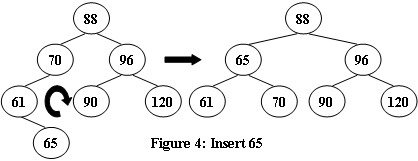
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
For each test case, print the root of the resulting AVL tree in one line.
5
88 70 61 96 120707
88 70 61 96 120 90 6588
自平衡搜索二叉树 AVL树
#include <iostream> using namespace std; typedef int ElementType; class tnode{ public: ElementType data; tnode* left{nullptr}; tnode* right{nullptr}; tnode()=default; tnode(int d):data{d}{}; }; class AVLtree { public: int size{0}; tnode* root{nullptr}; AVLtree():root{nullptr}{ } tnode* initiation(){ int n,temp; cin >> n; for(int i=0;i<n;i++){ cin >> temp; insertNode(temp); } return root; } int getHeight(tnode* p){ if(!p){ return -1; } return max(getHeight(p->left),getHeight(p->right))+1; } int getBalanceFactor(tnode* p){ if(!p){ return 0; } return getHeight(p->left)-getHeight(p->right); } //单左旋 tnode* leftRotate(tnode* p){ tnode* y=p->right; p->right=y->left; y->left=p; return y; } //单右旋 tnode* rightRotate(tnode* p){ tnode* y=p->left; p->left=y->right; y->right=p; return y; } tnode* insertNode(tnode* p,const int &n){ if(!p){ p = new tnode{n}; }else if(n<p->data){ p->left=insertNode(p->left, n); }else if(n>p->data){ p->right=insertNode(p->right, n); }else{ return p; } int balanceFactor=getBalanceFactor(p); if(balanceFactor>1){//左子树高-右子树高大于1 //左左 右旋 if(n<p->left->data){ return rightRotate(p); }else if(n>p->left->data){ //左右 先左旋 再右旋 p->left= leftRotate(p->left); return rightRotate(p); } }else if(balanceFactor<-1){ if(n>p->right->data){ return leftRotate(p); }else if(n<p->right->data){ p->right=rightRotate(p->right); return leftRotate(p); } } return p; } void insertNode(const int &n){ root=insertNode(root,n); } void deleteNode(){ } void searchNode(){ } //先左旋再右旋 tnode* LeftrightRotate(tnode* p){ return p; } //先右旋再左旋 tnode* rightLeftRotate(tnode* p){ return p; } void preOrderTraversal(){ } void inOrderTraversal(){ } void postOrderTraversal(){ } void getMaxNode(){ } void getMinNode(){ } bool isEmpty(){ return size==0; } }; int main(){ AVLtree t; cout << t.initiation()->data; return 0; }
数据结构 04-树5 Root of AVL Tree (25 分)
原文:https://www.cnblogs.com/ichiha/p/14783357.html