这是一道简单的算法题，17年的草稿

　　小姑娘问的问题。这贴被我编辑好后，一直都没放出来，可能是处于多种考虑吧，到底是为什么，我现在也记不清楚了。

首先观察规则

100 1 99 2 98 3 97 4 96 5 95 6 94 7 93 8 92 9 91 10 90 11 ...

显而易见：

偶数位 100 99 98 97 96...

奇数位 1   2   3   4   5...

题中要求空间复杂度O(1)，时间复杂度O(n)

用下面的代码可以实现，空间复杂度O(1)，时间复杂度O(n)： 

 1 #include<stdio.h>
 2 
 3 int main(void){
 4     int array[100];
 5     int max=100;
 6     int min =1;
 7     int i;
 8     for(i=0;i<=100;i+=2){
 9         array[i]=max--;
10         array[i+1]=min++;
11     }
12 
13     for(i=0;i<100;i++){
14         printf("%d ",array[i]);
15     }
16     return 0;
17 }

 运行结果：

以下内容为思维发散延伸篇(升序序列)：

然而，这让我想到一个问题，如何对一个等差（等比）数列重排，然后让排序后的结果是非等差（等比），任意数和邻近数字的差（比）都不相同？

想到这个问题，我陷入了深思中......

想想...

再想...

突然灵光一闪，例如等差数列：1, 2, 3, 4, 5, 6, 7, 8, 9, 10

假如先将它们前5位交换到它们的正确位置：

从后往前交换：

最终得到结果：

如果再将其奇数位从大到小排列可得：

那么整个流程大致是这个样子的：

为了验证这个猜想是否准确，我做了如下测试：

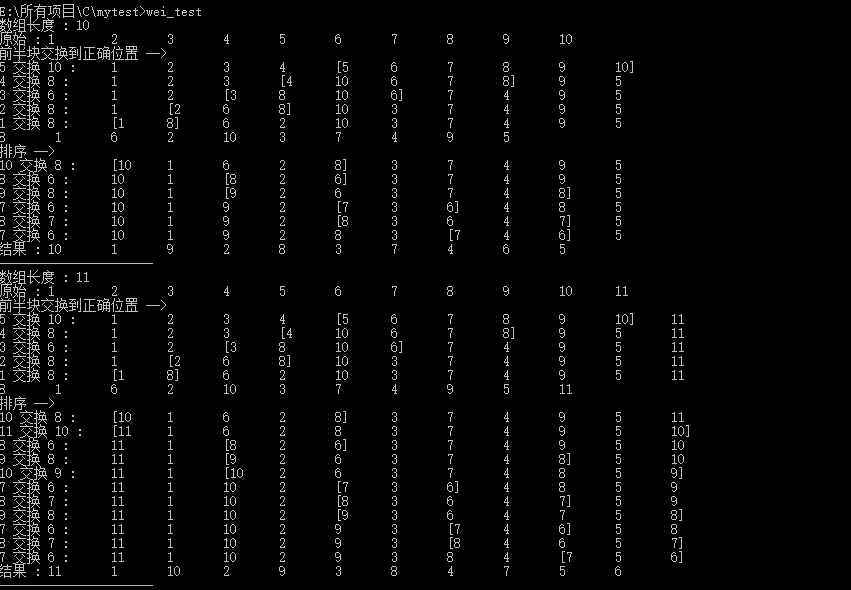
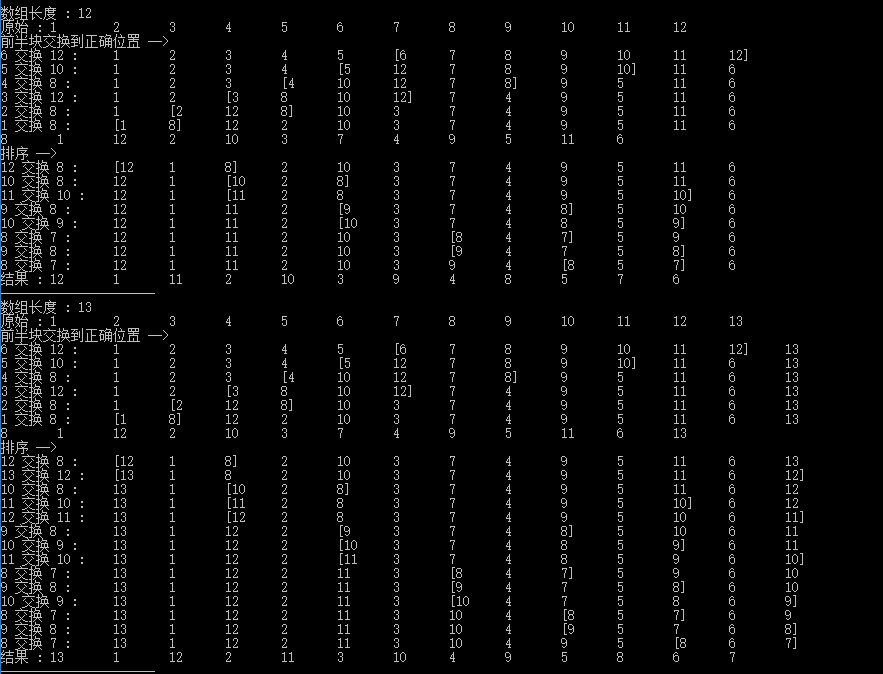
 在等差数列中 ，此公式是可行的。

(我不想试了，等比数列验证肯定也是可行的。)

这是一道简单的算法题，17年的草稿

原文：https://www.cnblogs.com/preacher/p/6841977.html