题目来自:http://218.5.5.242:9018/JudgeOnline/problem.php?id=1202
题目讲解:
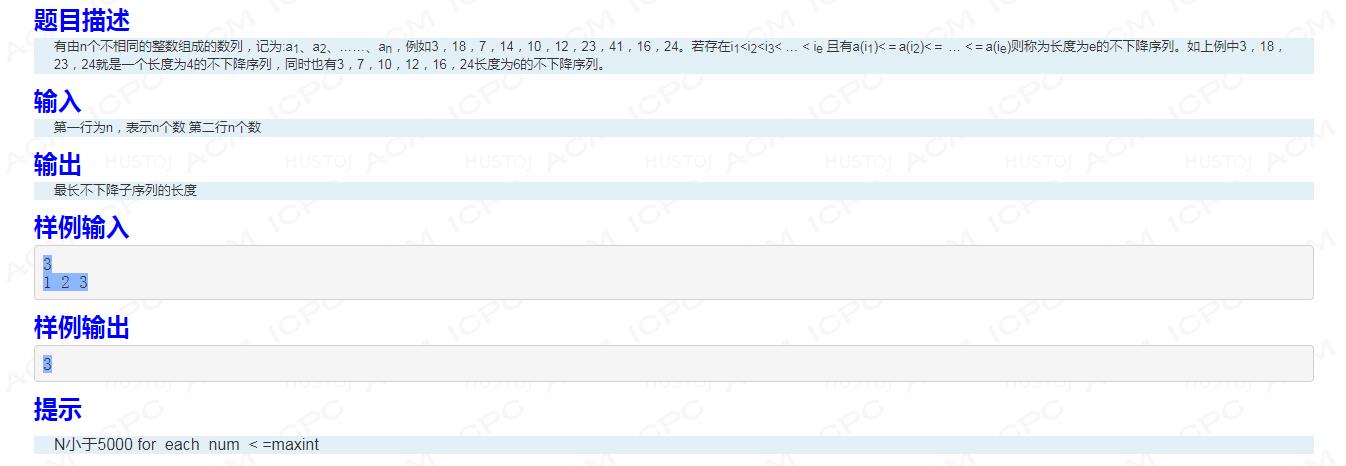
这道题是一道经典的DP最长上升子序列问题(LIS),我们设d(i)为该序列前i个元素的最长上升子序列,则状态转移方程也就不难列出来:d(i) = max{0,d(j) | j < i,ai <= aj},用a[i][0]表示原数,a[i][1]表示d(i),也可以列出一个表格:
| 元素(i) | 1 | 2 | 3 |
| A[i][0] | 1 | 3 | 2 |
| A[i][1] | 1 | 2 | 2 |
#include <iostream> #include <cstring> using namespace std; int main(){ int n,a[100001][2],ans = 0; cin >> n; a[0][0] = a[0][1] = 0; for (int i = 1;i <= n;i++) cin >> a[i][0]; for (int i = 1;i <= n;i++){ for (int j = i;j >= 0;j--){ if (a[i][0] >= a[j][0]) a[i][1] = max(a[i][1],a[j][1]+1); } } for (int i = 1;i <= n;i++) ans = max(ans,a[i][1]); cout << ans; return 0; }
原文:https://www.cnblogs.com/linyiweiblog/p/14799832.html