在图像处理中,对于直方图这个概念,肯定不会陌生。但是其原理真的可以信手拈来吗?
本文篇幅有点长,在此列个目录,大家可以跳着看:
(一)直方图的介绍
直方图到底可以干什么呢?我觉得最明显的作用就是有利于很直观的对图像进行分析了,直方图就像我们常用的统计图,直方图可以用来描述各种不同的事情,如物体的色彩分布、物体边缘梯度模板,以及表示目标位置的概率分布。
例如:我们统计了一个有11个学生的班级的身高和体重情况,身高为160cm的有5人,170cm的有4人,180cm的有2人。然后看体重,体重160斤的有3人,170斤的有5人,180斤的有3人。
用直方图统计就是这样:
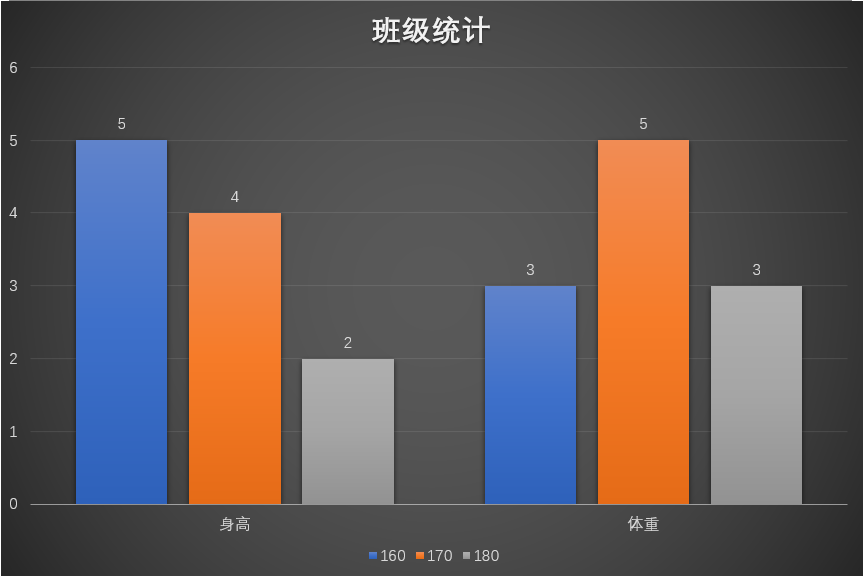
在opencv中,对于图像的直方图来说。对应上图数据,也有三个参数:
直方图的意义:
1. 直方图是图像中像素强度分布的图形表达方式。
2. 直方图统计了每一个强度值所具有的像素个数。
任一幅图像,都能唯一地算出一幅与它对应的直方图。但不同的图像,可能有相同的直方图。即图像与直方图之间是多对一的映射关系。
(二)直方图API
直方图是对数据的统计,并把统计值显示到事先设定好的bin(如上表,设置160,170,180)中,bin中的数值是从数据中计算出的特征的统计量。总之,直方图获取的是数据分布的统计图,通常直方图的维数要低于原始数据。
在OpenCV中封装了直方图的计算函数calcHist,为了更为通用,该函数的参数有些复杂,其声明如下:
calcHist( const Mat* images, //输入图像的数组(CV_8U,CV_16U,CV_32F) int nimages, //输入数组个数 const int* channels, //通道索引,可以传一个数组 {0, 1} 表示计算第0通道与第1通道的直方图,此数组长度要与histsize,ranges 数组长度一致 InputArray mask; //Mat(), //不使用腌膜 OutputArray hist, //输出的目标直方图,一个二维数组 int dims, //需要计算的直方图的维数 例如:灰度,R,G,B,H,S,V等数据 congst int* histSize, // 在每一维上直方图的个数。(简单把直方图看作一个一个的竖条的话,就是每一维上竖条的个数。) const float** ranges, //每一维数组的取值范围数组 bool uniform=true, bool accumulate = false );
opencv实现:
Mat src = imread("D:/opencv练习图片/src1.jpg"); imshow("原图片", src); // //步骤一:分通道显示 vector<Mat> bgr_plane; split(src, bgr_plane); //split//把多通道图像分为多个单通道图像 (const Mat &src, //输入图像 Mat* mvbegin //输出的通道图像数组) //步骤二:计算直方图 // 定义参数变量 const int channels[1] = { 0 }; const int bins[1] = { 256 }; float hranges[2] = { 0,255 }; const float* ranges[1] = { hranges }; Mat b_hist; Mat g_hist; Mat r_hist; // 计算Blue, Green, Red通道的直方图 calcHist(&bgr_plane[0], 1, 0, Mat(), b_hist, 1, bins, ranges); calcHist(&bgr_plane[1], 1, 0, Mat(), g_hist, 1, bins, ranges); calcHist(&bgr_plane[2], 1, 0, Mat(), r_hist, 1, bins, ranges); // 显示直方图 int hist_w = 512; int hist_h = 400; int bin_w = cvRound((double)hist_w / bins[0]);//直方图的等级 Mat histImage = Mat::zeros(hist_h, hist_w, CV_8UC3); // 归一化直方图数据(范围在0-400) normalize(b_hist, b_hist, 0, hist_h, NORM_MINMAX, -1, Mat()); normalize(g_hist, g_hist, 0, hist_h, NORM_MINMAX, -1, Mat()); normalize(r_hist, r_hist, 0, hist_h, NORM_MINMAX, -1, Mat()); //步骤三:绘制直方图并显示 for (int i = 1; i < bins[0]; i++) { line(histImage, Point(bin_w*(i - 1), hist_h - cvRound(b_hist.at<float>(i - 1))), Point(bin_w*(i), hist_h - cvRound(b_hist.at<float>(i))), Scalar(255, 0, 0), 2, 8, 0); line(histImage, Point(bin_w*(i - 1), hist_h - cvRound(g_hist.at<float>(i - 1))), Point(bin_w*(i), hist_h - cvRound(g_hist.at<float>(i))), Scalar(0, 255, 0), 2, 8, 0); line(histImage, Point(bin_w*(i - 1), hist_h - cvRound(r_hist.at<float>(i - 1))), Point(bin_w*(i), hist_h - cvRound(r_hist.at<float>(i))), Scalar(0, 0, 255), 2, 8, 0); } // 显示直方图 namedWindow("Histogram Demo", WINDOW_AUTOSIZE); imshow("Histogram Demo", histImage);
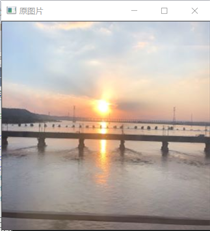
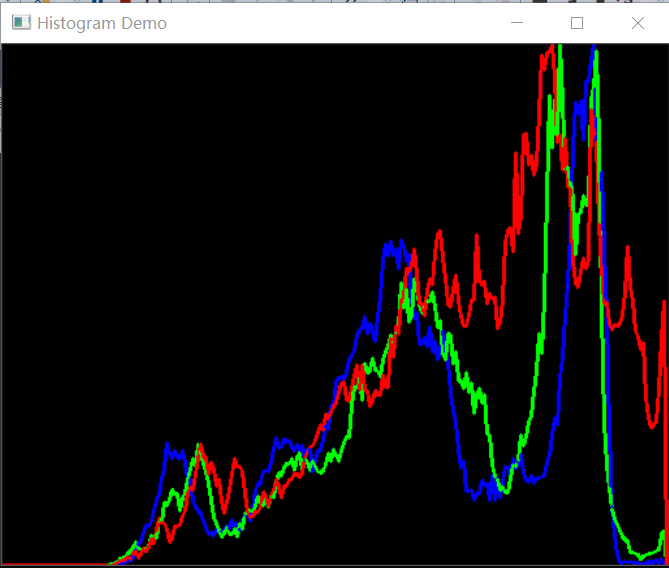
??在明白直方图的原理以后,那我们可不可以自己构造函数去实现对灰度图像的一维直方图绘制呢?
函数实现思想:(思想很重要!!)
opencv实现:
??主函数:
int main(int argc, char** argv) { Mat histogram_draw(Mat img, int *img_num); Mat src = imread("D:/opencv练习图片/直方图.png"); imshow("原图片", src); cvtColor(src, src, COLOR_RGB2GRAY); int img_num[256] = { 0 }; //定义一个存放统计数据的一维数组(256位,每位初始化为0) Mat histogram; //定义直方图 histogram = histogram_draw(src, img_num); imshow("直方图", histogram); waitKey(0); return 0; }
??自定义直方图函数:
//自定义直方图函数 //img:需要计算的图像 //img_num[]:计算直方图的特征空间子区段的数目 Mat histogram_draw(Mat img, int *img_num) { int r = 200; //定义高 int w = 1000; //定义宽 Mat histogram = Mat(r, w, CV_8UC3); //直方图画布 int row = img.rows; //图片的高度 int col = img.cols; //图片的宽度 for (int i = 0; i < row; i++) { for (int j = 0; j < col; j++) { int num = img.at<uchar>(i, j); //读取图片像素位置(i,j)处的灰度值 img_num[num]++; //将对应灰度值的个数加一(统计0-255的像素值的出现个数) } } int all = row * col; for (int i = 0; i < 256; i++) //对灰度值0-255循环处理 { int hight = int(double(img_num[i]) / double(all)*r); //(出现个数与总个数的比值)*高[即各灰度值所占的比值的高度] //opencv图像的像素坐标系原点在左上角 Point ps(i * 4, r); Point pe(i * 4, r - hight*10); line(histogram, pe, ps, Scalar(0, 0, 255)); } return histogram; }

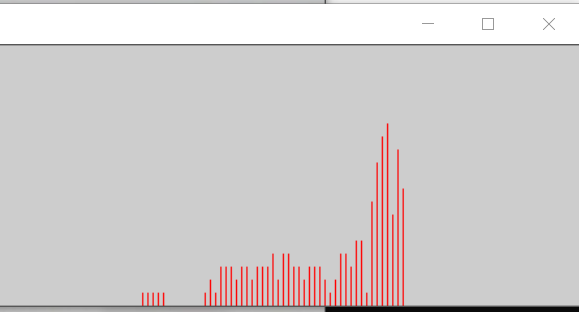
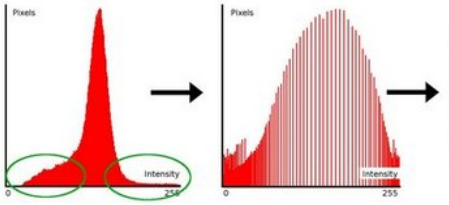
直方图均衡化是灰度变换的一个重要应用,广泛应用于图像增强处理中。它是通过拉伸像素强度分布范围来增强图像对比度的一种方法。
说得更清楚一些, 以直方图为例, 你可以看到像素主要集中在中间的一些强度值上. 直方图均衡化要做的就是 拉伸 这个范围. 见下面左图: 绿圈圈出了 少有像素分布其上的 强度值. 对其应用均衡化后, 得到了中间图所示的直方图。
直方图均衡化的API非常简单:(输入图像必须是单通道)
void equalizeHist(InputArray src, OutputArray dst) //第一个参数,源图像,需为8位单通道图像 //第二个参数,输出图像,尺寸、类型和源图像一致
??opencv对于彩色(三通道)的图像如何均衡化呢?
灰常简单:先将三通道拆分为3个单通道split(),再分别对其均衡化,最后合并为三通道merge()。
Mat dst; Mat src = imread("D:/opencv练习图片/直方图.png"); imshow("原图片", src); //分割通道 vector<Mat>channels; split(src, channels); Mat blue, green, red; blue = channels.at(0); green = channels.at(1); red = channels.at(2); //分别对BGR通道做直方图均衡化 equalizeHist(blue, blue); equalizeHist(green, green); equalizeHist(red, red); //合并通道 merge(channels, dst); imshow("output", dst);


直方图的反向投影
直方图反向投影用于图像分割或在图像中用直方图查找感兴趣的对象。
直方图在一定程度上可以反应图像的特征,我们截取一个有固定特征的样本图,比如草地,然后计算该块草地的直方图,然后用这个直方图去和整幅图像的直方图做对比,根据一定的判断条件,就能得出相似的即为草地。

是不是看起来像是语义分割?
其实一定意义上这就是语义分割,这不过直方图反向分割的依据是人为计算的(直方图),后者分割的依据是靠在神经网络中学习得来的。
??先来一看下opencv中直方图反向投影的API:
void calcBackProject( const Mat * images, //要进行投影的输入图像的地址,注意该API要求输入的是地址 int nimages,//输入图像的数目 const int * channels,//要进行投影的通道数 InputArray hist,//样本的直方图 OutputArray backProject,//输出得反向投影,为Mat类型 const float ** ranges, //输入直方图得特征空间的取值范围 double scale = 1, bool uniform = true )
??该API实现的原理:
假设我们现在有一个四行四列得灰度图,它得灰度值如下图:
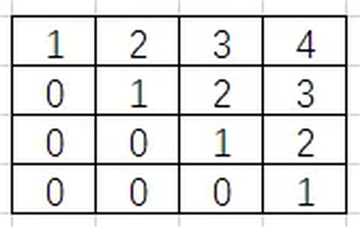
说这幅图有什么特征呢?直观上看类似于一个边角,但这是直观上,怎么表示出来呢?深度学习是靠神经网络黑箱计算出来得,我们可以用直方图。
那我们就计算这幅灰度图得直方图,如果以组距为1计算直方图并反向投影到原图,得到得为下图:
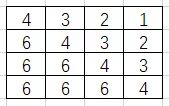
大概表述一下边角的特征:左下角有6个像素值相同得三角形区域,中间斜向下有四个像素值相同得边界线,以此类推。这就是用直方图得到边角的特征。
那如果以组距为2计算直方图呢?反向投影后为:
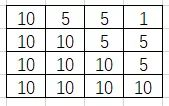
可以看到特征描述得更为广泛了,就像深度学习里,提取更高层次的特征,虽然更为普适,但也会忽略掉一些细节特征。
我们就是拿这个反向投影所表达的特征信息,去和整幅图做对比,来得到特征相似的部分,达到分割的效果。
?? 利用反向投影进行语义分割(opencv实现)
先看一下我们今天要处理得图片:
目的:将公路提取出来
 样本图片:
样本图片:
(一)先读取原图以及样本图,并转换为HSV格式。
Mat src1 = imread("D:/opencv练习图片/直方图反向投影.jpg");//原图 Mat src2 = imread("D:/opencv练习图片/样本图.jpg");//样本图 imshow("原图", src1); //转换为HSV图像 Mat HsvImage, RoiImage_HSV; cvtColor(src1, HsvImage, COLOR_BGR2HSV); cvtColor(src2, RoiImage_HSV, COLOR_BGR2HSV);
为什么转HSV呢?
因为HSV表达颜色更为方便区分,我们今天只对前两个通道直方图统计:H(色调)和S(饱和度),不用V(亮度)。
(二)计算样本图的直方图并进行归一化
Mat roiHist; //直方图对象 int dims = 2; //特征数目(直方图维度) float hranges[] = { 0,180 }; //特征空间的取值范围 float Sranges[] = { 0,256 }; const float *ranges[] = { hranges,Sranges }; int size[] = { 20,32 }; //存放每个维度的直方图的尺寸的数组 int channels[] = { 0,1 }; //通道数 calcHist(&RoiImage_HSV, 1, channels, Mat(), roiHist, dims, size, ranges); //直方图归一化 normalize(roiHist, roiHist, 0, 255, NORM_MINMAX);
为什么要归一化呢,直方图反向投影到原图后,原图各位置表示的是整幅图中等于该点像素值的数量,归一化后就变成概率了。
(三)将计算的归一化后的直方图进行反向投影
//反向投影 Mat proImage; //投影输出图像 calcBackProject(&HsvImage, 1, channels, roiHist, proImage, ranges); imshow("反向投影", proImage);

可以看到,公路的轮廓以及提取出来了(虽然效果不是太好,肯定不如深度学习。。。)
(四)用掩码将公路给抠出来显示
//图像掩码Mask操作 threshold(proImage, proImage, 50, 255, THRESH_BINARY);//对mask进行二值化,将mask进一步处理 Mat dstImage = Mat::zeros(src1.size(), CV_8UC3); src1.copyTo(dstImage, proImage); imshow("结果", dstImage);

后期再加上些边缘检测和霍夫直线变换,和一些其他骚操作,就可以提取公路啊,车道线啥的了。
参考链接:(8条消息) 直方图的反向投影的原理_michaelhan3的博客-CSDN博客_直方图反向投影
原文:https://www.cnblogs.com/xyf327/p/14799533.html