1. 向量
1.1 向量与点
向量和点到底有什么区别?
从计算的角度来说,没有。因为计算机里对一个三维点和三维向量都存的是三个浮点数。从数学概念的角度来说,当然有。所谓向量代表的是位移。为什么教科书上说,一个向量可以随便移动?因为它代表的是位移嘛,表示的是一个相对的东西。而所谓的点呢?它代表的是坐标系里的一个绝对位置,不能随便改变的。
向量代表方向(往哪里走),点代表位置(呆在哪里)。
1.2 坐标系
(只讨论笛卡尔坐标系)
多坐标空间是实时渲染里的数学基础。为什么要用多个坐标空间?因为相对位置在很多情况下要方便。
多坐标系让人迷惑的第一点就是:世界坐标系只有一个。这里世界坐标系的含义是,原点在零点的那个坐标系。或许称它为尺度更合适。也就是说,无论你要定义什么坐标系,你的原点和轴都得有数字表示吧,而你选这些数字都是相对我而言的。
明确了世界坐标系后,就可以开始讨论其它坐标系了。首先,定义一个坐标系的要素是:原点和坐标轴。坐标轴一般都是相互正交的。
这里的原点是一个点,而坐标轴是向量(更具体地说,单位向量)。有了原点和坐标轴,其他任意的点和向量都可以用它们来表示出来。所以就有了书里常见的几种写法,它们都是等价的(符号游戏)。
一定一个三维坐标系,它包括一个原点和三个坐标轴:
\[o = (o_x, o_y, o_z) \\vec{i} = (i_x, i_y, i_z) \\vec{j} = (j_x, j_y, j_z) \\vec{k} = (k_x, k_y, k_z)
\]
坐标系里的向量表示:
\[\vec{v} = (v_x, v_y, v_z) \= v_x \vec{i} + v_y \vec{j} + v_z \vec{k} + o \=
v_x\left(\begin{matrix}i_x\\i_y\\i_z\end{matrix}\right) +
v_y\left(\begin{matrix}j_x\\j_y\\j_z\end{matrix}\right) +
v_z\left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right) +
\left(\begin{matrix}o_x\\o_y\\o_z\end{matrix}\right) \=
v_x\left(\begin{matrix}i_x,i_y,i_z\end{matrix}\right) +
v_y\left(\begin{matrix}j_x,j_y,j_z\end{matrix}\right) +
v_z\left(\begin{matrix}k_x,k_y,k_z\end{matrix}\right) +
\left(\begin{matrix}o_x,o_y,o_z\end{matrix}\right)
\]
1.3 坐标系转换
那么多坐标系之间如何转换呢?如果转换不了,或者不方便,那多坐标系有什么好的呢?所以坐标系转换当然是直观而且便于运算的。拿二维坐标系举例。如下图,定义了两个坐标系:Frame W(世界坐标系)和 Frame A。
\[\textbf{Frame W} \o = (0,0) \quad \vec{i} = (1, 0) \quad \vec{j} = (0, 1) \\textbf{Frame A} \o_A = (2,3) \quad \vec{i_A} = (-1, 0) \quad \vec{j_A} = (0, -1)
\]
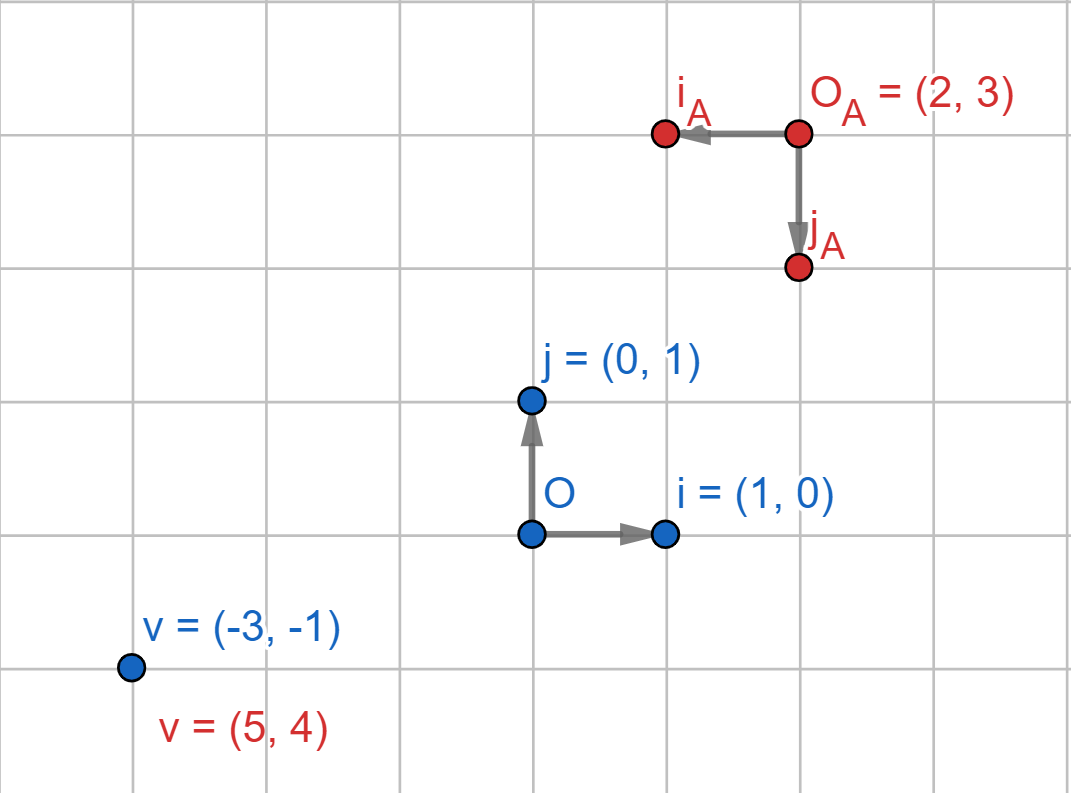
Frame W 中的有个点 v = (-3,-1),求:在 Frame A 中 v = ?
首先来看这个点的等价写法:
\[\vec{v} = v_x \vec{i} + v_y \vec{j} + o \= v_x(i_x,i_y) + v_y(j_x,j_y) + (o_x,o_y)
\\ \Leftrightarrow
(-3,-1) = -3(1,0) + -1(0,1) + (0,0)
\]
现在来引入齐次坐标。齐次坐标简单来说就是多用一个维度,比如用四维向量来表示三维向量。实际的三维向量通过将四维向量的前三维都除以第四维得到。
\[\vec{v} = (v_x, v_y, v_z, v_w) \Leftrightarrow (\frac{v_x}{v_w}, \frac{v_y}{v_w}, \frac{v_z}{v_w})
\]
对于点,w=1;对于向量,w=0。用零点或零向量则依情况而定。齐次坐标等价写法:
\[(v_x,v_y,1) = v_x (i_x,i_y,0) + v_y (j_x,j_y,0) + (o_x,o_y,1)
\\ \Leftrightarrow
(-3,-1,1) = -3(1,0,0) + -1(0,1,0) + (0,0,1)
\]
接着来引入矩阵。向量是特殊的矩阵,向量是“一个维度”的,而矩阵是“两个维度的”。同样,在计算机眼里它们都是一堆数字,给它们赋予含义的是数学。引入矩阵如何使得计算变得更直观?回到点的等价表示上:
\[(v_x,v_y,1) = v_x (i_x,i_y,0) + v_y (j_x,j_y,0) + (o_x,o_y,1)
\]
如果把等式右边的行向量从上到下叠起来,再把系数往左移到一起,最后把圆括号换成方括号,就会变成(矩阵出现了!):
\[\left[\begin{matrix}v_x & v_y & 1\end{matrix}\right] = \left[\begin{matrix}v_x & v_y & 1\end{matrix}\right]
\left[\begin{matrix}i_x & i_y & 0 \\ j_x & j_y & 0 \\ o_x & o_y & 1\end{matrix}\right]
= \left[\begin{matrix} (\vec{i},0) \\ (\vec{j},0) \\ ({\bf{o}},1)\end{matrix}\right]
\]
在 Frame A 里,应该有着相似的形式:
\[\left[\begin{matrix}v_x & v_y & 1\end{matrix}\right] = \left[\begin{matrix}v_Ax & v_Ay & 1\end{matrix}\right]
\left[\begin{matrix}i_Ax & i_Ay & 0 \\ j_Ax & j_Ay & 0 \\ o_Ax & o_Ay & 1\end{matrix}\right]
= \left[\begin{matrix} (\vec{i_A},0) \\ (\vec{j_A},0) \\ ({\bf{o_A}},1)\end{matrix}\right]
\\ \Leftrightarrow
\left[\begin{matrix}-3 & -1 & 1\end{matrix}\right] = \left[\begin{matrix}5 & 4 & 1\end{matrix}\right]
\left[\begin{matrix}-1 & 0 & 0 \\ 0 & -1 & 0 \\ 2 & 3 & 1\end{matrix}\right]
\\ \Leftrightarrow
\left[\begin{matrix}v_x & v_y & 1\end{matrix}\right] = \left[\begin{matrix}v_Ax & v_Ay & 1\end{matrix}\right] M_A
\]
运用一下矩阵的运算法则:
\[\left[\begin{matrix}v_x & v_y & 1\end{matrix}\right] M^{-1}_A = \left[\begin{matrix}v_Ax & v_Ay & 1\end{matrix}\right] M_A M^{-1}_A \\Longleftrightarrow
\left[\begin{matrix}v_Ax & v_Ay & 1\end{matrix}\right] = \left[\begin{matrix}v_x & v_y & 1\end{matrix}\right] M^{-1}_A
\]
举个例子,在 这篇博客 里,构建 M_view 的时候,我们是要把 V_world 的点转换到 V_view 里去。按照上面这个式子,有:
\[\left[\begin{matrix}v_{x_{world}} & v_{y_{world}} & 1\end{matrix}\right] = \left[\begin{matrix}v_{x_{view}} & v_{y_{view}} & 1\end{matrix}\right]
\left[\begin{matrix} \vec{u} & 0 \\ \vec{v} & 0 \\ \bf{Q} & 1\end{matrix}\right]
\\ \Leftrightarrow
{v_{world}}= {v_{view}} {M_{view}}^{-1}
\\ \Leftrightarrow
\left[\begin{matrix}v_{x_{view}} & v_{y_{view}} & 1\end{matrix}\right] = \left[\begin{matrix}v_{x_{world}} & v_{y_{world}} & 1\end{matrix}\right]
\left[\begin{matrix} \vec{u} & \vec{v} & 0\\ - {\bf{Q}}\vec{u} & - {\bf{Q}} \vec{v} & 1\end{matrix}\right]
\\ \Leftrightarrow
{v_{view}}= {v_{world}} M_{view}
\]
所以为什么要求坐标轴要正交?因为正交的话,逆矩阵就等于转置矩阵,算转置可比求逆容易多了。
1.4 变换
当前语境下的变换,就是点位置的改变。大致有两条路来得到,描述点位置变化的矩阵:
- 点从一个坐标系转换到另一个坐标系:需要知道目标坐标系的参数(视图变换适用,如上节的例子所示)
- 进行多少缩放操作?平移多少?旋转多少?(所有变换都适用,在 这篇博客 里介绍了用组合操作的方法如何推导出 M_view)
对第 2 条路,最常见的变换操作是缩放和旋转,属于线性变换。因为它们只能做到:
\[x‘ = ax + by \\ y‘ = cx + dy \\Leftrightarrow
\left[\begin{matrix}x‘ & y‘\end{matrix}\right] = \left[\begin{matrix}x & y\end{matrix}\right] \left[\begin{matrix}a & b \\ c & d\end{matrix}\right]
\]
而平移变换,属于仿射变换,因为它可以做到:
\[x‘ = ax + by + e \\ y‘ = cx + dy + f \\Leftrightarrow
\left[\begin{matrix}x‘ & y‘ & 1\end{matrix}\right] = \left[\begin{matrix}x & y & 1\end{matrix}\right] \left[\begin{matrix}a & b & 0\\ c & d & 0 \\ e & f & 1\end{matrix}\right]
\]
这样引入齐次坐标的理由就显而易见了:一个矩阵就能装下最常用的三个变换。
点、向量与坐标系
原文:https://www.cnblogs.com/tandandan/p/14803904.html
