一、题目描述

计数质数

> 统计所有小于非负整数 n 的质数的数量。
>
> 示例 1：
>
> 输入：n = 10
> 输出：4
> 解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
> 示例 2：
>
> 输入：n = 0
> 输出：0
> 示例 3：
>
> 输入：n = 1
> 输出：0
>
>
> 提示：
>
> 0 <= n <= 5 * 106
>

二、思路分析

• 获得小于n的非负数中质数的个数。首先我们得知道什么叫质数（除了1和自己本身以外不能被其他数整除的叫做质数）
• 首先就是暴露破解。咋一看感觉除了暴力破解也没其他办法了。暴力实现的方式也很简单两层循环就可以解决了。

public int countPrimes(int n) {
    int total = 0;
    for (int i = 2; i < n; i++) {
        int j=2;
        for (j = 2; j < i; j++) {
            if (i % j == 0) {
                break;
            }
        }
        if (j == i) {
            total++;
        }
    }
    return total;
}

• 之前也提到过算法考察的思维并不是解决问题。上面的暴力方法贴到leetcode上是这个结果

• 就算是leetcode通过，这种解法也不是最优的。

三、升级之路+AC代码

减少暴力次数

• 不知道大家有没有发现比如6有哪些数据相乘得到。仔细观察上图会发现在2之后其实就是重复。

• 其实最终的临界值就是6的开发。根号6之后就会出现重复的数据。所以我们在算一个数是否是质数的时候只需要循环截止到根号

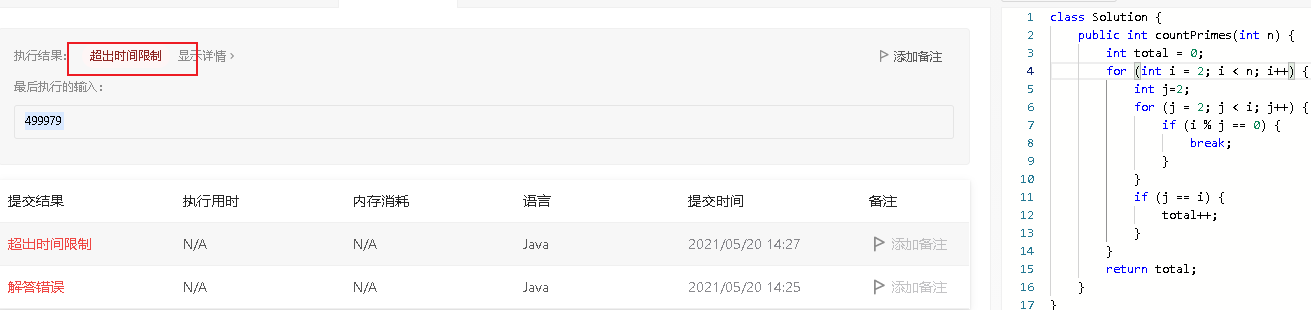
public int countPrimes(int n) {
    int total = 0;
    for (int i = 2; i < n; i++) {
        boolean flag = false;
        for (int j = 2; j*j <= i; j++) {
            if (i % j == 0) {
                flag=true;
                break;
            }
        }
        if (!flag) {
            total++;
        }
    }
    return total;
}

• 上述我们将改到根号，但是到leetcode上运行结果依旧是超时。此次升级以失败告终。

埃筛法

• 说实话本题虽然是简单题，但是对于我这样的新手来说一开始的确没实现出来。当看了官方的题解思路之后才知道埃筛法。
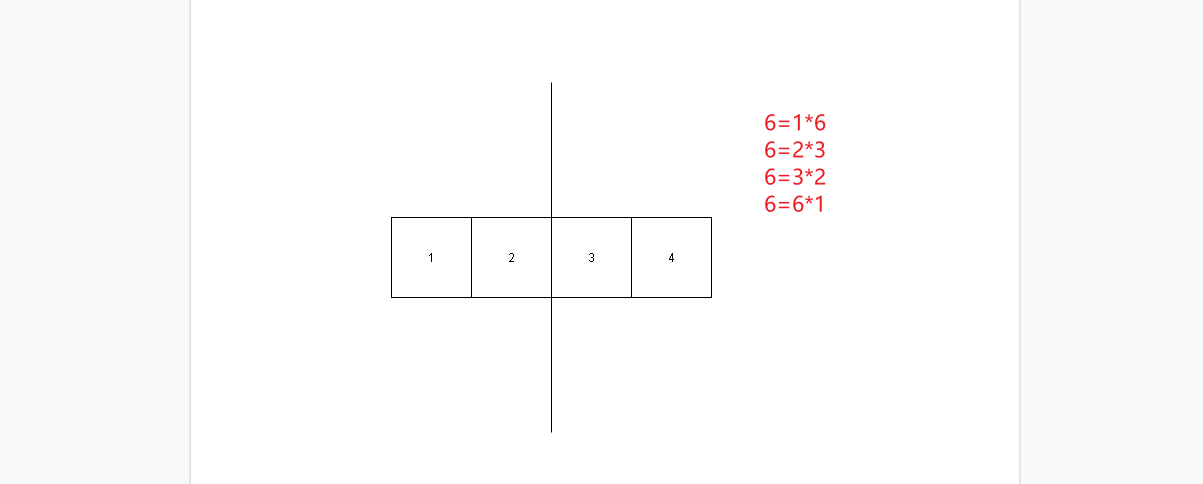
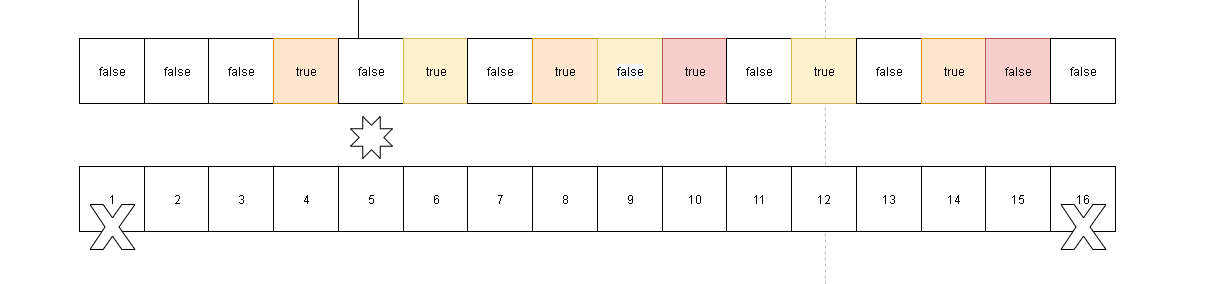
• 埃筛法就是考虑到数据之间存在关联性。比如说我们检测到3是质数，那么1*3;2*3;3*3......;n*3这些数据都是合数，在循环检测中就不需要在判断他们是不是质数了。这样就大大的减少了我们排查的次数

• 当我们检测2是质数时，对应的4，6,8,10,12,14都将被标记为合数。因为题目考核的是n以下的数字，所以这里16不需要考虑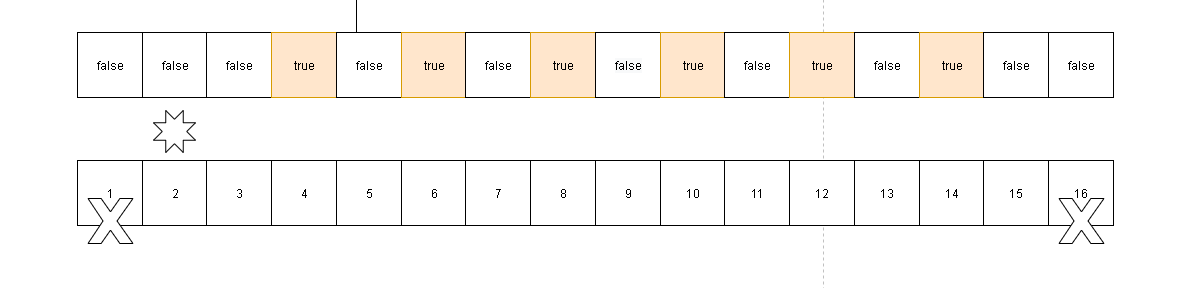

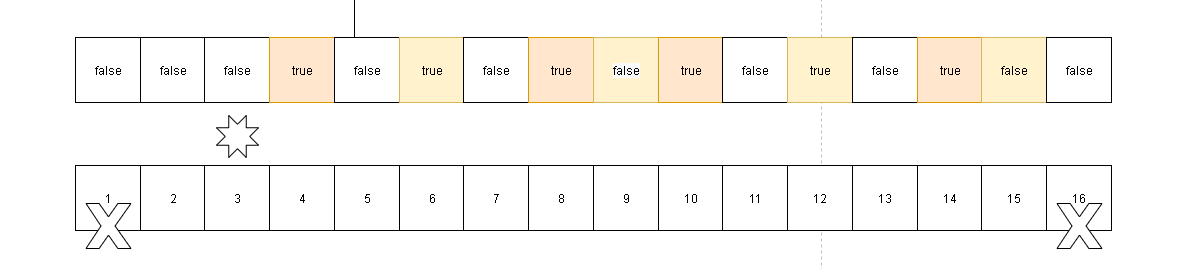
• 然后我们继续根据3找到对应的合数。

• 在走到4这个节点，因为节点4默认是false但是被标记为true，说明节点4被前面的质数计算过是合数，所以我们这里跳过。我们很明确的知道下面将通过5来进行延伸

• 后面就是对7,11,13进行延伸，这里就不做演示了

public int countPrimes2(int n) {
    int total = 0;
    //构造同等长度的状态位数组， 默认false表示质数
    boolean[] primes = new boolean[n];
    for (int i = 2; i < n; i++) {
        if (!primes[i]) {
            total++;
            for (int j = 2 * i; j < n; j += i) {
                primes[j] = true;
            }
        }
    }
    return total;
}

埃筛法2

• 虽然埃筛法已经完成了leetcode的检验。但是在执行上还是有提高的空间。而且我们在分析下埃筛法的执行过程不难发现好多数据是重复的。
• 在上面的演示图中我也是通过不同颜色来区分不同质数的延伸的。比如说10第一次被2*5的2质数渲染成合数了。但是10会再次被5*2渲染合数。这个道理和上面暴力法升级中是同样的问题。为了避免类似10=2*5 ，乘数位置交换的问题，我们可以在延伸的时候从质数的平方开始，因为质数的之前肯定会被之前的质数渲染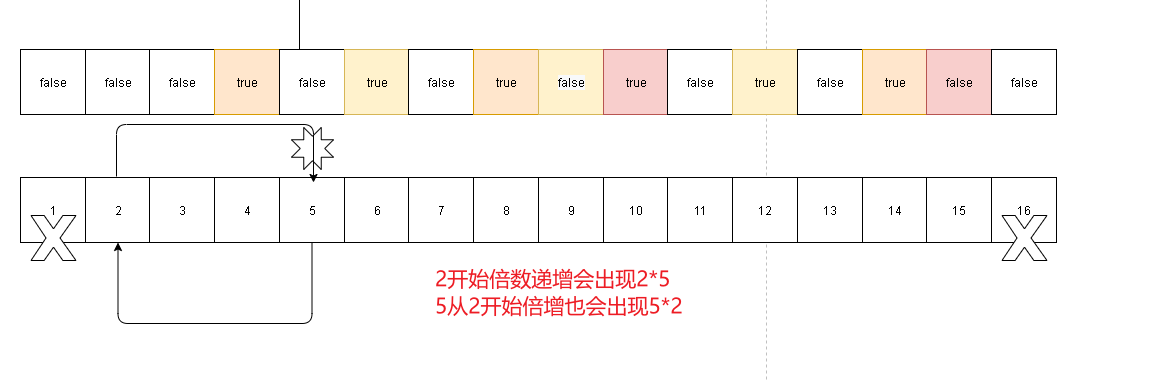

public int countPrimes3(int n) {
    int total = 0;
    //构造同等长度的状态位数组， 默认false表示质数
    boolean[] primes = new boolean[n];
    for (int i = 2; i < n; i++) {
        if (!primes[i]) {
            total++;
            if ((long)i * i >= n) {
                continue;
            }
            for (int j = i * i; j < n; j += i) {
                //System.out.println("index="+j+"i="+i);
                primes[j] = true;
            }
        }
    }
    return total;
}

• 诶筛法升级在时间和空间上都有少许的提升。不过诶筛法升级之后需要处理数组越界的情况。因为进行了平方操作。

四、总结

• 为什么选择这题讲解呢？是因为一开始看到这题的时候除了暴力法没有想到其他的方法(说到底是自己的算法不行)
• 其次是该算法考虑到数据之间的关联性。通过关联避免我们遍历次数。实际上还是暴力法只不过是在暴力法的基础上不断进行优化减少次数

leetcode204--计算范围内的质数个数,尽可能避免循环次数

原文：https://www.cnblogs.com/zhangxinhua/p/14803913.html