------------恢复内容开始------------
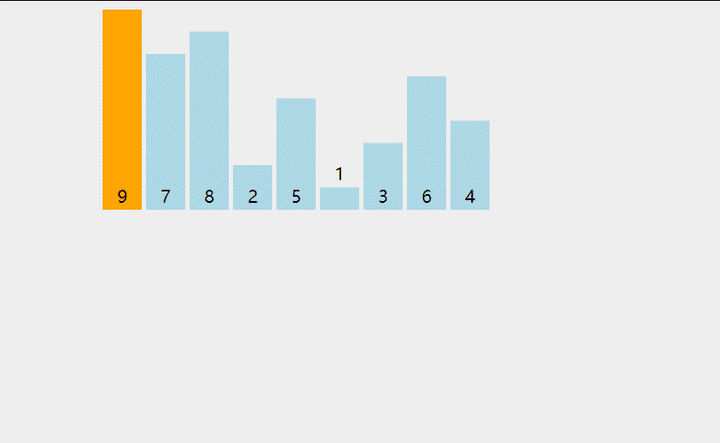
几个概念 1、稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 仍然在 b 的前面,则为稳定排序。 2、非稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为非稳定排序。 3、原地排序:原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。 4、非原地排序:需要利用额外的数组来辅助排序。 ## 1.冒泡 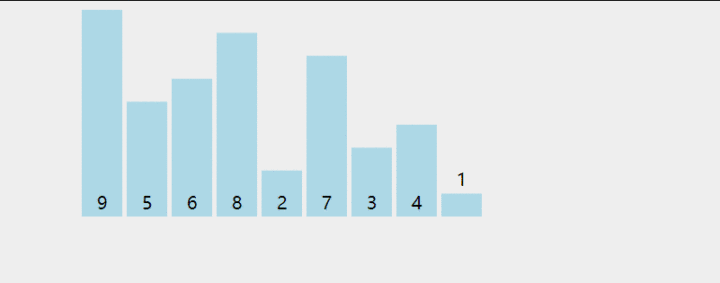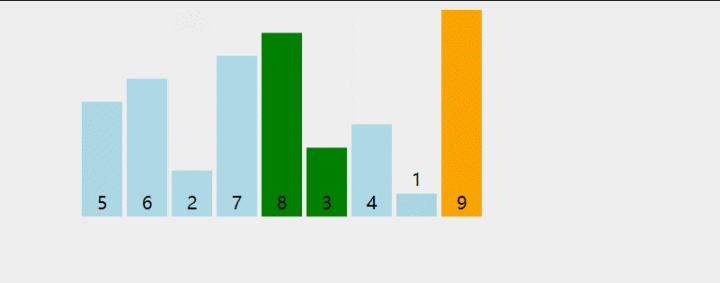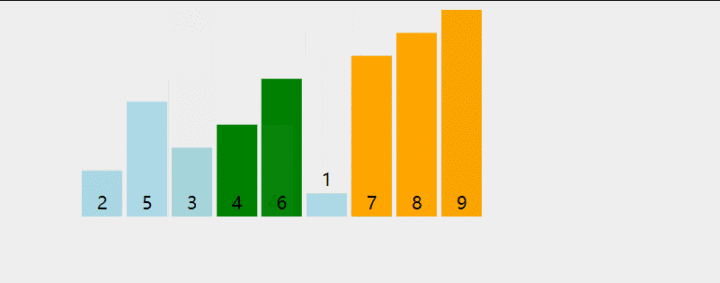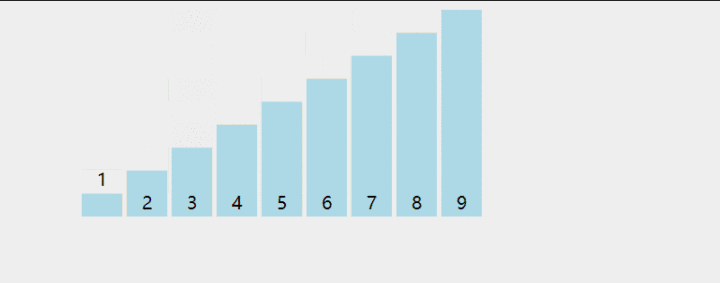 思想:把第一个元素与第二个元素比较,如果第一个比第二个大,则交换他们的位置。接着继续比较第二个与第三个元素,如果第二个比第三个大,则交换他们的位置.... ### 未优化 ``` int [] arry={2,4,1,0,8,5}; int n=arry.length; int temp; for (int i = 0; i2、把它与左边第一个元素比较,如果左边第一个元素比它大,则继续与左边第二个元素比较下去,直到遇到不比它大的元素,然后插到这个元素的右边。
3、继续选取第3,4,....n个元素,重复步骤 2 ,选择适当的位置插入。
交换结束的条件:
1.左边没有数可以比较了。
2.不比左边的数小了。
(想象下打斗地主的情景)
let a = [1,4,5,1,2,9,0,3];
for(let i=1;i<a.length;i++){
for(let j=i-1;j>=0 && a[j]>a[j+1]; j--){
//这里用了解构来交换值
[a[j],a[j+1]]=[a[j+1],a[j]];
}
}
性质:
1、时间复杂度:O(N*N)
最坏:4 5 6 7 3 2 1 O(N*N)
最好:1 2 3 4 5 6 7 O(N)不需要交换
2、空间复杂度:O(1) 3、稳定排序 4、原地排序
注意这里不能自己写个swap()函数来交换,牵扯到作用域的问题。
交换两个值有很多方法!
思路:
1.在未排序的数列中找到最小(or最大)元素,然后将其存放到数列的起始位置
2.再从剩余未排序的元素中继续寻找最小(or最大)元素,然后放到已排序序列的末尾。
3.以此类推,直到所有元素均排序完毕。
let a = [1,4,5,1,2,9,0,3];
let min;//无序区的最小值
let i;//有序区的末尾位置
let j;//无序区的开始位置
for( i=0;i<a.length;i++){
min=i;
//找出a[i+1]-a[n]之间最小的元素
for(j=i+1;j<a.length;j++){
if(a[j]<a[min]){
//更新无序区最小值的位置
min=j;
}
}
//若min!=i,则交换 a[i] 和 a[min]。
//交换后,保证了a[0]..a[i]之间元素有序
if(min!=i){
[a[min],a[i]]=[a[i],a[min]];
}
}
性质:1、时间复杂度:O(n2) 2、空间复杂度:O(1) 4、原地排序
稳定性得具体问题具体分析
不同的实现方法有不同的结果.
思路:
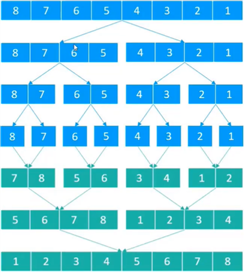
function merge(arry,left,mid,right){
let size=right-left+1;
let help=new Array(size);
let p1=left;
let p2=mid+1;
let i=0;
while(p1<=mid && p2<=right){
help[i++]=arry[p1]<arry[p2]?arry[p1++]:arry[p2++];
}
while(p1<=mid){
help[i++]=arry[p1++];
}
while(p2<=right){
help[i++]=arry[p2++];
}
for(let j=0;j<help.length;j++){
arry[left+j]=help[j];
}
}
function sort(arry,left,right){
if(left === right){
return;
}else {
let mid = left + Math.floor((right - left) / 2);
sort(arry, left, mid);
sort(arry, mid + 1, right);
merge(arry, left, mid, right);
}
}
let a = [1,4,5,1,2,9,0,3];
sort(a,0,a.length-1);
console.log(a);
let mid = left + Math.floor((right - left) / 2);
这里一定注意下!
------------恢复内容结束------------
原文:https://www.cnblogs.com/My-Coding-Life/p/14810161.html