三角函数的定义

前言

任何事物都是在发展中不断地完善的，数学概念的学习和理解也是一样的，我们以三角函数的定义为例，加以说明；

概念沿革

• 初中定义：由于受初中学生的认知能力和角的范围的限制，我们只能在 \(Rt\triangle\) 中定义三角函数[用形来定义]：

这种定义方式，其缺陷是三角函数的自变量 \(\theta\) 的范围只能是 \([0^{\circ}，90^{\circ}]\)，而高中数学中的角的范围已经扩充到了 \((-\infty，+\infty)\) ，显然上述的初中定义已经不能用了，需要更新，应该怎么更新呢？

• 高中定义：将角放置到平面直角坐标系中，初始边放置到\(x\)轴的非负半轴上，终边随其落在某个象限或者坐标轴上，然后在终边上任取一点(不是原点) \(P(x，y)\) ，则 \(r=|OP|=\sqrt{x^2+y^2}\) ，则[用数来定义]：

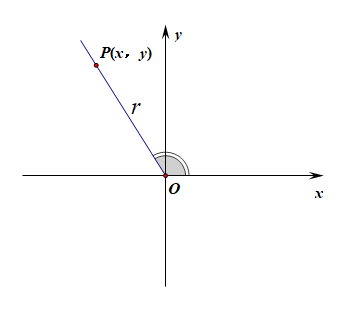
很显然，这种定义方式可以刻画 \((-\infty，+\infty)\) 范围内的任意一个角的三角函数，而且兼容范围 \([0^{\circ}，90^{\circ}]\) ，也就是说高中的三角函数的定义同样能解释初中的三角函数的定义，体现了数学概念发展的扬弃。

典例剖析

在平面直角坐标系中，角 \(\alpha\) 的顶点在坐标原点，始边与 \(x\) 轴的非负半轴重合，若角 \(\alpha\) 的终边经过点 \(P\)\((\sin47^{\circ}\)\(,\)\(\cos47^{\circ})\) ，则 \(\sin(\alpha-13^{\circ})\)的值为【\(\quad\)】

法1：利用三角函数的定义，令 \(P(x,y)\) ，则可知 \(x=\sin47^{\circ}\) ， \(y=\cos47^{\circ}\)，

则 \(r=|OP|=\sqrt{\sin^247^{\circ}+\cos^247^{\circ}}=1\)，

故 \(\sin\alpha=\cfrac{y}{r}=\cos47^{\circ}\) ， \(\cos\alpha=\cfrac{x}{r}=\sin47^{\circ}\) ，

则\(\sin(\alpha-13^{\circ})=\sin\alpha\cos13^{\circ}-\cos\alpha\sin13^{\circ}\)

\(=\cos47^{\circ}\cos13^{\circ}-\sin47^{\circ}\sin13^{\circ}\)

\(=\cos(47^{\circ}+13^{\circ})=\cos60^{\circ}=\cfrac{1}{2}\)，故选 \(A\).

法2：借助单位圆上点的坐标， 由于 \(\sin47^{\circ}=\cos43^{\circ}\)， \(\cos47^{\circ}=\sin43^{\circ}\)，

点 \(P\) 的坐标为 \((\cos43^{\circ},\sin43^{\circ})\) ，即 \(\alpha=43^{\circ}\)，

[或 \(\alpha=k\times 360^{\circ}+43^{\circ}\)，\(k\in Z\)，此处从简，取\(k=0\) ]

故 \(\sin(\alpha-13^{\circ})=\sin(43^{\circ}-13^{\circ})=\sin30^{\circ}=\cfrac{1}{2}\)，故选 \(A\).

三角函数的定义

原文：https://www.cnblogs.com/wanghai0666/p/13305466.html