任何事物都是在发展中不断地完善的,数学概念的学习和理解也是一样的,我们以三角函数的定义为例,加以说明;
##? 概念沿革
*? 初中定义:由于受初中学生的认知能力和角的范围的限制,我们只能在 $Rt\triangle$ 中定义三角函数[用形来定义]:
$\sin\theta=\cfrac{对边}{斜边} ,\quad\cos\theta=\cfrac{邻边}{斜边},\quad\tan\theta=\cfrac{对边}{邻边}$?
这种定义方式,其缺陷是三角函数的自变量 $\theta$ 的范围只能是 $[0^{\circ},90^{\circ}]$,而高中数学中的角的范围已经扩充到了 $(-\infty,+\infty)$ ,显然上述的初中定义已经不能用了,需要更新,应该怎么更新呢?
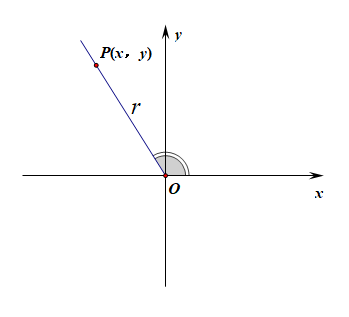
*? 高中定义:将角放置到平面直角坐标系中,初始边放置到$x$轴的非负半轴上,终边随其落在某个象限或者坐标轴上,然后在终边上任取一点(不是原点) $P(x,y)$ ,则 $r=|OP|=\sqrt{x^2+y^2}$ ,则[用数来定义]:
$$\sin\theta=\cfrac{y}{r} ,\quad \cos\theta=\cfrac{x}{r} , \quad\tan\theta=\cfrac{y}{x}$$
很显然,这种定义方式可以刻画 $(-\infty,+\infty)$ 范围内的任意一个角的三角函数,而且兼容范围 $[0^{\circ},90^{\circ}]$ ,也就是说高中的三角函数的定义同样能解释初中的三角函数的定义,体现了数学概念发展的扬弃。
## 典例剖析
在平面直角坐标系中,角 $\alpha$ 的顶点在坐标原点,始边与 $x$ 轴的非负半轴重合,若角 $\alpha$ 的终边经过点 $P$$(\sin47^{\circ}$$,$$\cos47^{\circ})$ ,则 $\sin(\alpha-13^{\circ})$的值为【$\quad$】
$A.\cfrac{1}{2}$? $B.\cfrac{\sqrt{3}}{2}$? $C.-\cfrac{1}{2}$? $D.-\cfrac{\sqrt{3}}{2}$
? ??
法1:利用三角函数的定义,令 $P(x,y)$ ,则可知 $x=\sin47^{\circ}$ , $y=\cos47^{\circ}$,
则 $r=|OP|=\sqrt{\sin^247^{\circ}+\cos^247^{\circ}}=1$,
故 $\sin\alpha=\cfrac{y}{r}=\cos47^{\circ}$ , $\cos\alpha=\cfrac{x}{r}=\sin47^{\circ}$ ,
则$\sin(\alpha-13^{\circ})=\sin\alpha\cos13^{\circ}-\cos\alpha\sin13^{\circ}$
$=\cos47^{\circ}\cos13^{\circ}-\sin47^{\circ}\sin13^{\circ}$
$=\cos(47^{\circ}+13^{\circ})=\cos60^{\circ}=\cfrac{1}{2}$,故选 $A$.
法2:借助单位圆上点的坐标, 由于 $\sin47^{\circ}=\cos43^{\circ}$, $\cos47^{\circ}=\sin43^{\circ}$,
点 $P$ 的坐标为 $(\cos43^{\circ},\sin43^{\circ})$ ,即 $\alpha=43^{\circ}$,
[或? $\alpha=k\times 360^{\circ}+43^{\circ}$,$k\in Z$,此处从简,取$k=0$ ]
故? $\sin(\alpha-13^{\circ})=\sin(43^{\circ}-13^{\circ})=\sin30^{\circ}=\cfrac{1}{2}$,故选 $A$.
原文:https://blog.51cto.com/wanghai0666/2817664