思维导图

4.1 线性判据基本概念

生成模型：

给定训练样本{Xn},直接在输入空间内学习其概率密度函数p(x)。

• 优势：
  可以根据p(x)采样新的样本数据。
  可以检测出较低概率的数据，实现离群点检测。

• 劣势：
  如果是高维的x，需要大量训练样本才能准确的估计p(x) ;否则，会出现维度灾难问题。

判别模型：

给定训练样本{Xn},直接在输入空间内估计后验概率p(Ci|x)。
在分类任务中，后验概率分布p(Ci|x)相当于直接从输入样本x映射到类别输出Ci的判别函数f(x),即判别模型。

• 优势：
  快速直接、省去了耗时的高维观测似然概率估计。
  （在分类任务中，观测概率分布所包含的大量复杂内容有时对于后验概率的影响比较有限。）
  最简单的判别模型：线性判据
  如果判别模型f(x)是线性函数，则f(x)为线性判据。
  可以用于两类分类，决策边界是线性的，也可以用于多类分类,相邻两类之间的决策边界也是线性的。

• 优势：
  计算量少:在学习和分类过程中，线性判据方法都比基于学习概率分布的方法计算量少。
  适用于训练样本较少的情况

模型：

判别公式：

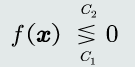
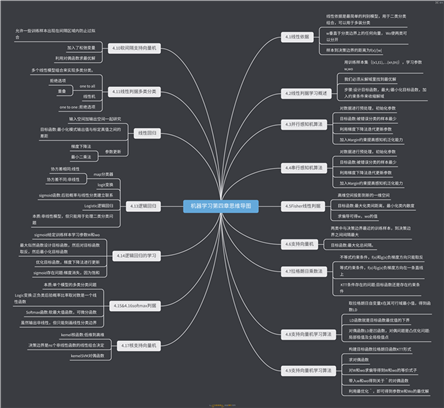
决策边界就是令f(x)=0（是d维空间上的超平面）
其中：w垂直与决策边界的任何向量。（决定了决策边界的方向）
Wo决定了决策边界的偏移量，使其能够满足两个类输出值分别为正负。它决定了决策边界相对于坐标原点的位置。

任意样本x到决策边界的垂直距离r为：

r值越大，这个点属于正类或者负类的程度越大。

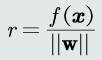
f(x)是样本x到决策面的代数距离度量。

4.2 线性判据学习概述

线性判据的学习和识别过程：

• 以监督式学习为例：
• 基于训练样本{x1, x2, ... XN }及其标签{t1,t2...,tN},设计目标函数，学习W和Wo。

识别过程(将待识别样本x带入训练好的判据方程)：

由于训练样本个数通常会远远大于参数个数(w的维度+ wo的维度)，所以线性判据满足条件的解不唯一。学习算法就是要找到一个最优解。
针对两类(正负类)分类，方便起见，将负类的输出值取反，则得到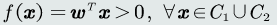

给定N个训练样本，参数向量w的解域位于N个超平面正半部分的交集。

找最优解的方法：

• 设计目标函数：
  目标函数反映了如何实现有效决策的核心思想。
  目标函数的求解就是最小化/最大化目标函数。
  有
  解析求解：求关于训练参数的偏导，并设置偏导为0
  迭代求解:先猜测参数初始值，然后不断的根据当前计算得到的更新值迭代更新参数。

• 加入约束条件
  可以提高泛化能力，使得解域范围收缩。

4.3 并行感知机算法

根据目标函数的不同，可以设计不同的线性判据算法。

• 预处理

• • 目的：根据标记过的训练样本{(xn,tn)},学习模型参数: W, Wo
    首先将两个参数合为一个参数,线性判据改写为:
    
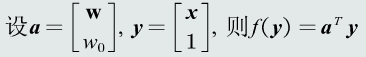
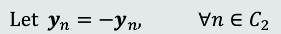    再将C2类的训练样本全部取反:从而得到：预处理后两个类的输出值都是正数。

• 目标函数
  被错误分类的样本，输出值f(n)是负数。且输出值的绝对值越大，错误的程度越大。

• 目标函数:针对所有被错误分类的训练样本(即输出值小于0的训练样本)其输出值取反求和

• 最小化该目标函数:取目标函数关于α的偏导(即梯度)：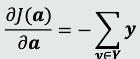

使用梯度下降法更新参数。
每个维度的梯度反方向就是该维度往目标函数最小值收敛的最速下降方向。
更新的大小:每个维度的梯度幅值代表参数在该维度上的更新程度。（通常加入步长来调整更新的幅度）

• 参数更新
  

4.4 串行感知机算法

目标函数:如果当前训练样本被错误分类，最小化其输出值取反:

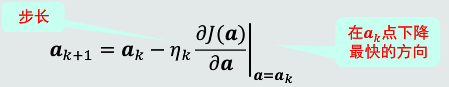
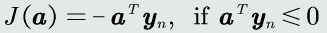
最小化目标函数，还是取关于α参数向量的偏导。
偏导不含有α，所以还是使用梯度下降法求解。
步长决定收敛的速度、以及是否收敛到局部或者全局最优点。
当样本位于决策边界边缘时，对该样本的决策有很大的不确定性。

加入margin约束条件，将错误分类的标准改为:

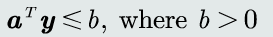
这里b的作用是避免出现α=0的解，提高泛化能力。

4.5 Fisher线性判据

线性判据的模型可以看做是把原空间各点x投影到新的一维空间y。
找到一个最合适的投影轴，使两类样本在该轴上投影的重叠部分最少（用两类样本分布的均值之差度量）,同时使得各自类内样本分布的离散程度尽可能小（用每类样本分布的协方差矩阵表示），从而使分类效果达到最佳。

最大化该目标函数：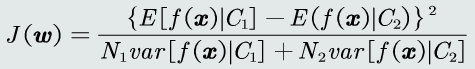
求解w的最优解，将所有样本的均值投影到坐标原点，得到Wo。

• Fisher线性判据：
  
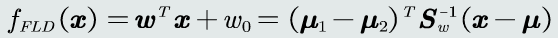
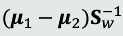  决策边界就是令上式x=0。该决策边界就是过u，斜率为的超平面。

4.6 支持向量机基本概念
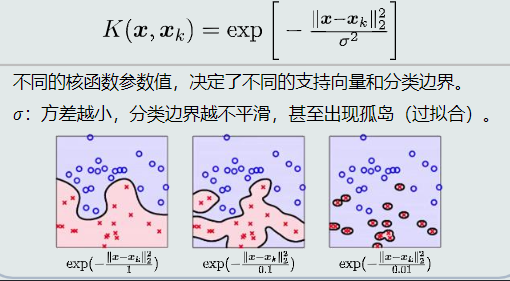
给定一组训练样本，使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大。
在支持向量机中，正负类训练样本输出真值分别用+1和-1来表达。
给定标记过的训练样本{(xn, tn)},线性分类器可以表达为:

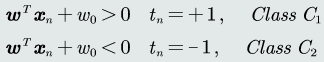
加入间隔的概念，引入一个正常数▲，分类器进一步表达为:

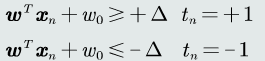
意味着没有训练样本落在间隔范围内

• 目标函数
  目标：最大化总间隔，等价于最小化||w||

目标函数：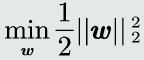

同时满足约束条件: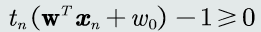这里假设 ??=1

4.7 拉格朗日乘数法

等式约束优化问题：

min f(x)
s.t. g(x)=0
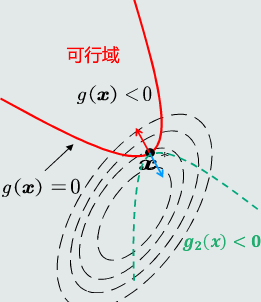
可行域：g(x)=0的区域。
函数在等高面上任意一点的梯度方向与其等高面(切线方向)正交，且朝向( 即正方向)函数值较高的方向。f(x)的极值点x必须位于曲线g(x)=0上。
搜寻极值点x:沿着g(x)=0的切线方向、向着f(x)负梯度方向移动。当出现沿着切线方向、无法再向f(x)负梯度方向移动时停止。

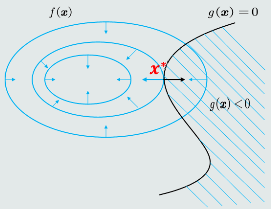
此时，在该点f(x)等高线与g(x)=0相切，即f(x)与g(x)梯度方向在同一直线上，该点为f(x)的极值点x。
f(x)与g(x)的梯度记作

如果是等式约束，在极值点x上，
的方向必然平行，可能同向或反向，梯度的幅值可能不同。

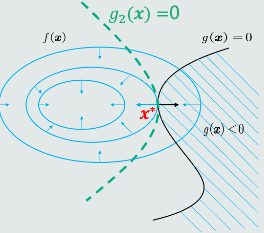
存在一个
使得：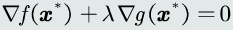

可以定义一个拉格朗日函数：

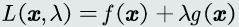
拉格朗日函数满足驻点条件和约束条件:

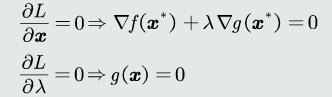
等式约束问题可以转换为等价的不带约束的优化问题。

不等式约束优化问题：

min f(x)
s.t. g(x)≤0
可行域：g(x)≤0的区域。
1、极值点落在可行域内：
此时约束条件不起作用。
直接通过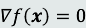
获得极值点。同上。
2、极值点落在可行域边界：
即极值点位于区域g(x)=0区域。
搜寻极值点x:当出现沿着g(x)=0切线方向、无法再向f(x)负梯度方向移动时停止。在该点f(x)等高线与g(x)=0相切，该点为f(x)的极值点x。对于不等式约束，在极值点x*，f(x)与g(x)的负梯度方向平行且相反。

总结：无论是g(x)<0 (λ=0)还是g(x)=0 (λ>0)的约束情况，始终存在一个λ≥0 (对偶可行性), 满足:

4.8 拉格朗日对偶问题

对偶函数：主问题的最优值下界

对偶函数LD是拉格朗日函数L的逐点最小值函数。

逐点最小值函数min是凹函数。

由于逐点最大化函数是凹函数，且拉格朗日函数可以看做关于对偶变量的仿射组合，故对偶函数LD是凹函数。

由于目标函数LD是凹函数，约束条件是凸函数，所以对偶问题是凸优化问题。

强对偶性：如果强对偶性成立，则对偶问题获得主问题的最优下界。

4.9 支持向量机学习算法

支持向量机目标函数的求解：带不等式约束的优化问题使用拉格朗日对偶法求解。

对偶问题的求解：二次规划问题+参数最优化。

w最优解

决策过程：?? 和 ??0 的学习过程实际上是从训练样本中选择一组支持向量，并将这些支持向量存储下来，用作线性分类器。

4.10 软间隔支持向量机

软间隔：克服过拟合。

软间隔克服过拟合的原理：可以将SVM的硬间隔（hard margin）放宽到软间隔（soft margin），允许一些训练样本出现在间隔区域内，从而具备一定的克服过拟合的能力)

设计思想：引入松弛变量。

分类器表达

设计过程：构建目标函数->构建拉格朗日函数->构建对偶函数(在极值点得到对偶函数LD)

4.11 线性判据多类分类

多类分类的本质：非线性

实现非线性分类的途径：一个模型：能刻化非线性的决策边界。

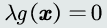
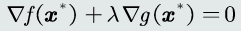
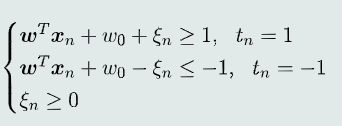
多个模型：多个模型（线性/非线性）组合成非线性决策边界。

组合方式：并行组合、串行组合。

思路一：One-to-all

假设条件：假设每个类与剩余类可分，总共需要训练K个分类器。
问题：每个分类器的正负类样本个数不均衡。
混淆区域问题：拒绝选项；重叠。

思路二：线性机

假设条件：每个类与剩余类线性可分。
训练：基于one-to-all策略训练??个线性分类器????，每个分类器对应一个类????。
决策：使用输出值投票法（max函数）给定测试样本??，其属于所有分类器中输出值最大的那个类。

取输出值最大：该值最大表示属于该类的可能性越大。

线性机 = ??个线性模型 + 一个max函数
max是非线性的，因此线性机可以实现非线性分类。
通过max函数的引入，线性机将特征空间最终分为??个决策区域。
决策边界??????垂直于超平面(???? ? ????)
输出值投票法：使用两类权重??向量的差值决定相邻两类之间的决策边界；
标签识别法：利用每一类的权重??向量决定该类与剩余类之间的决策边界。

线性机的优势：由于使用max函数，不再有混淆区域（即拒绝区域和重叠区域）。通过划定相邻两类之间的边界，分割了重叠区域和拒绝区域。

线性机的问题：可能出现最大的????(??) ≤ 0，即测试样本??出现在拒绝区域。如果严格按照线性判据的定义，拒绝区域其实是线性机（基于one-to-all策略）无法正确判断的区域。

思路三：one-to-one策略

基本思想：针对每两个类???? 和???? ，训练一个线性分类器：?????? ?? = ?????????? + ??0????。????类真值为正；????类真值为负。总共需要训练??(?? ? 1) /2个分类器。
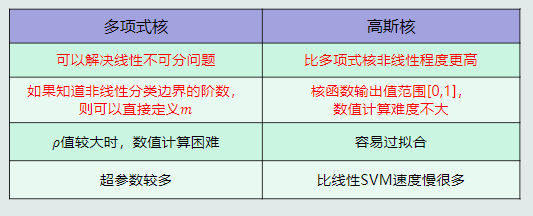
优势：适用于一些线性不可分的情况，从而实现非线性分类；与one-to-all策略相比，不再有重叠区域。
问题：会出现拒绝选项，即样本不属于任何类的情况。

总结

• 使用线性判据进行多类分类，本质上是利用多个线性模型组合而成一个非线性分类器。因此，决策边界不再是由单个超平面决定，而是由多个超平面组合共同切割特征空间。

4.12 线性回归

输入样本：个数与特征维度的关系

线性回归模型表达

线性回归和线性判据的模型对比

线性回归模型学什么：给定训练样本，学习参数W。

线性回归模型学习过程：学习参数(给定学习样本学习参数w)->给定N个训练样本->目标函数(最小化均方误差)

目标函数的对比

目标优化过程：展开目标函数->对参数w求偏导->目标优化（梯度下降法）->最小二乘法

线性回归的概率解释

目标函数优化：似然函数；最大似然估计；目标似然/MSE。

最大似然等同于最小化均方误差(MSE)。

4.13 逻辑回归的概念

典型模型的属性

MAP分类器

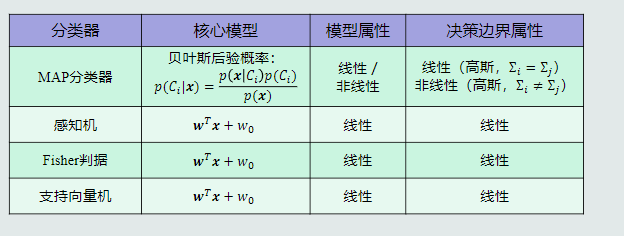
如果两个类别数据分布的协方差矩阵不同（即Σ?? ≠ Σ??），则MAP分类器的决策边界是一个超二次型曲面，即非线性。
如果两个类别数据分布的协方差矩阵相同（即Σ?? = Σ?? ），则MAP分类器的决策边界是一个超平面，即线性。

Logit变换：??1类的后验概率与??2类的后验概率之间的对数比率

• 对于二类分类，MAP分类器通过比较后验概率的大小来决策。
  在每类数据是高斯分布且协方差矩阵相同的情况下，由于Logit变换等同于线性判据的输出，所以在此情况下Logit(z) 是线性的。

Sigmoid函数：连接线性模型和后验概率的桥梁

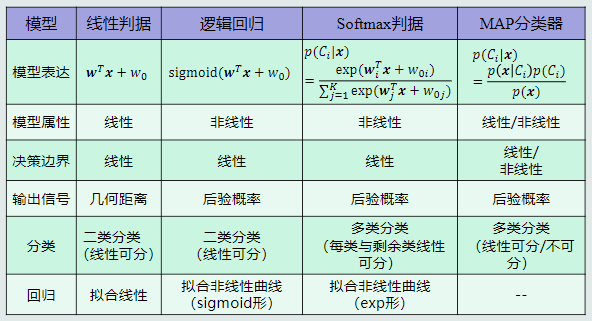
线性模型??(??) + Sigmoid函数 = 后验概率

逻辑回归：线性模型??(??) + sigmoid函数。

决策边界：单个逻辑回归可以用于二类分类；给定两个类，逻辑回归的决策边界仍然是线性的超平面。

逻辑回归总结：

• 逻辑回归本身是一个非线性模型。
  逻辑回归用于分类：仍然只能处理两个类别线性可分的情况。但是，sigmoid函数输出了后验概率，使得逻辑回归成为一个非线性模型。因此，逻辑回归比线性模型向前迈进了一步。
  逻辑回归用于拟合：可以拟合有限的非线性曲线。

4.14 逻辑回归的学习

学什么：给定训练样本，学习参数??和??0。

训练样本：

• 正类（??1类）样本的输出真值???? = 1；
• 负类（??2类）样本的输出真值???? = 0。
• 注意：这种真值取值方式与SVM不一样。

最大似然估计法：给定单个输入样本??，模型输出的类别标签??可以看做一个随机变量。

交叉熵：交叉熵可以用来度量两种分布的差异程度。

目标函数：给定??个训练样本，把每个训练样本的交叉熵求和，得到最终的目标函数：

目标函数优化：梯度下降法；

步骤：对参数w求偏导；对参数w0求偏导；参数更新：采用梯度下降法更新w和w0;

4.15 Softmax判据的概念

逻辑回归输出：属于正类的后验概率

后验概率的多类情况：一个类与剩余类的后验概率比率。

逻辑回归是由Logit变换反推出来的。

由Logit变换可知：正负类后验概率比率的对数是一个线性函数。

分类??个类，可以构建??个线性判据。第??个线性判据表示????类与剩余类的分类边界，剩余类用一个参考负类（reference class） ????来表达。

对于多类分类，K个线性模型也跟每个类对应的后验概率建立起了联系。

Softmax判据：??个线性判据 + softmax函数。

Softmax判据用于分类，等同于基于one-to-all策略的线性机。

适用范围：分类、回归

• 总结
  Softmax判据本身是一个非线性模型。
  Softmax判据用于分类：只能处理多个类别、每个类别与剩余类线性可分的情况。但是， Softmax判据可以输出后验概率。因此，Softmax判据比基于one-to-all策略的线性机向前迈进了一步。
  Softmax判据用于拟合：可以输出有限的非线性曲线。

• 模型对比
  

4.16 Softmax判据的学习

学什么：给定训练样本，学习K组参数

目标函数：最大似然估计。针对所有训练样本，最大化输出标签分布的似然函数，以此求得参数的最优值。似然函数为所有训练样本输出概率的乘积。

判别式学习是依赖所有类的训练样本来学习参数。

Softmax：针对每个输出类别分别计算梯度值，但每个参数的梯度值与所有类别样本都相关。

4.17 核支持向量机

Kernel方法的基本思想：如果样本在原始特征空间（??空间）线性不可分，可以将这些样本通过一个函数??映射到一个高维的特征空间（Φ空间），使得在这个高维空间，这些样本拥有一个线性分类边界。

核函数：在低维X空间的一个非线性函数，包含向量映射和点积功能，即作为X空间两个向量的度量，来表达映射到高维空间的向量之间的点积。

Kernel SVM的决策是关于测试样本x与Ns个支持向量xk的核函数的线性组合，即Ns个非线性函数的线性组合。

常见核函数 多项式核函数：

高斯核函数

核函数的优缺点

第四章 线性判据与回归

原文：https://www.cnblogs.com/dishao/p/14814499.html